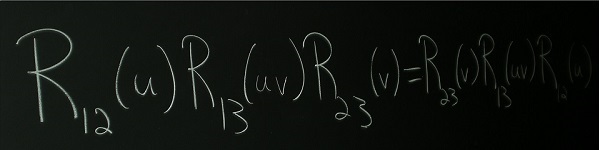
Abstracts of publications and preprints
Highest weight modules over the quantum periplectic superalgebra pdf : We begin the study of highest weight representations of the quantized enveloping superalgebra of type P. We introduce a Drinfeld-Jimbo representation and establish a triangular decomposition. We explain how to relate modules over the quantized enveloping superalgebra of type P to modules over the corresponding Lie superalgebra, and we prove that the category of tensor modules is not semisimple.
Quantized enveloping superalgebra of type P pdf : We introduce a new quantized enveloping superalgebra attached to the Lie superalgebra of type P which provides a quantization of a certain Lie bisuperalgebra structure and we study its basic properties. We also introduce the periplectic q-Brauer algebra and prove that it is the centralizer of the quantized enveloping superalgebra action on tensor powers of the natural representation. We end by proposing a definition for a new periplectic q-Schur superalgebra.
Vertex representations for Yangians of Kac-Moody algebras pdf : Using vertex operators, we build representations of the Yangian of a simply laced Kac-Moody algebra and of its double. As a corollary, we prove the PBW property for simple laced affine Yangians.
Representations of twisted Yangians of types B, C, D: II pdf : We continue the study of finite-dimensional irreducible representations of twisted Yangians associated to symmetric pairs of types B, C and D, with focus on those of types BI, CII and DI. After establishing that, for all twisted Yangians of these types, the highest weight of such a module necessarily satisfies a certain set of relations, we classify the finite-dimensional irreducible representations of twisted Yangians for the pairs (soN,soN-2 + so2) and (so2n+1,so2n).
Equivalences between three presentations of orthogonal and symplectic Yangians pdf : We prove the equivalence of two presentations of the Yangian of a simple Lie algebra and we also show the equivalence with a third presentation when the Lie algebra is either orthogonal or symplectic. As an application, we obtain an explicit correspondence between the two versions of the classification theorem of finite-dimensional irreducible modules for orthogonal and symplectic Yangians.
Representations of twisted Yangians of types B, C, D: I pdf: We develop a theory of highest weight representations for twisted Yangians of types B, C, D and we classify the finite-dimensional irreducible representations of twisted Yangians associated to symmetric pairs of types CI, DIII and BCD0.
Local Weyl modules and cyclicity of tensor products for Yangians pdf: We provide a sufficient condition for the cyclicity of an ordered tensor product of fundamental representations of a Yangian associated to a simple Lie algebra. When this Lie algebra is classical, we make the cyclicity condition concrete, which leads to an irreducibility criterion for the ordered tensor product. We show that every local Weyl module is isomorphic to an ordered tensor product of fundamental representations of the Yangian.
Twisted Yangians of small rank pdf: We establish isomorphisms between certain twisted Yangians of rank one or two introduced in the paper "Yangians for symmetric pairs of types B,C,D" and corresponding twisted Yangians for symmetric pairs of types AI and AII introduced originally by G. Olshanski.
Twisted Yangians for symmetric pairs of types B,C,D pdf: We study coideal subalgebras of the extended Yangians of type B,C,D associated to appropriate solutions of the reflection equation. Those subalgebras can be viewed as twisted Yangians for the symmetric pairs of type BDI, CI, CII and DIII in Cartan's classification.
On deformed double current algebras of simple Lie algebras pdf: We prove the equivalence of two definitions of deformed double current algebras associated to a semisimple Lie algebra. One definition was proposed by myself in Quantum algebras and quivers by considering a certain degeneration of an affine Yangian, the other one arose in recent work of V. Toledano Laredo and Y. Yang on elliptic Casimir connections. We also construct a certain central element and prove that, in type A and for certain values of the deformation parameters, the center of a deformed double current algebra contains two polynomial rings in infinitely many variables.
From twisted quantum loop algebras to twisted Yangians pdf
: We prove how the Yangian of gl_n in its RTT presentation and how Olshanski's twisted Yangians for the orthogonal and symplectic Lie algebras can be obtained by a degeneration process from quantum loop algebras and some of their twisted analogues.
Almost cellular algebras pdf: We obtain results on algebras which have all the properties of cellular algebras except for the existence of a certain anti-involution. We apply them to the quantum walled Brauer-Clifford superalgebras studied in the next paper below.
Quantum Walled Brauer-Clifford Superalgebras pdf: We introduce a family of associative superalgebras which are analogues of the quantum walled Brauer algebras and are q-deformations of the walled Brauer superalgebras. These new superalgebras are described explicitly via generators and relations. We show that they are isomorphic to the centralizer algebras of the action of quantum superalgebras of type Q on mixed tensor spaces. We obtain for them a diagrammatic presentation and prove that they are almost cellular. We are also led to define q-Schur superalgebras of type Q and prove for them a super analog of a classical result for q-Schur algebras using a quantization of the algebra of regular functions on the space of supermatrices of type Q.
Vertex operators for Yangians of Kac-Moody algebras (in preparation): We construct vertex operator representations for Yangians of simply-laced Kac-Moody algebras and use these, along with the coproduct in the preprint below, to prove the PBW property of those Yangians.
Coproduct for Yangians of Kac-Moody algebras pdf: We construct a new coproduct on (completed) Yangians associated to affine Kac-Moody algebras. We also produce a presentation of Yangians of symmetrizable Kac-Moody algebras which may be of independent interest.
Quantum superalgebras of type P (in preparation)
: We introduce a quantized enveloping superalgebra of type P similar to Olshanski's quantized enveloping superalgebra of type Q. It is defined via an RTT-relation, using a suitable solution of the quantum Yang-Baxter equation.
Twisted Yangians, twisted quantum loop algebras and affine Hecke algebras of type BC pdf
: We study twisted Yangians of type AIII which have appeared in
the literature under the name of reflection algebras. They admit
q-versions which are new twisted quantum loop algebras. We explain how
these can be defined equivalently either via the reflection equation or
as coideal subalgebras of Yangians of gl_n (resp. quantum loop algebras
of gl_n). The connection with affine Hecke algebras of type BC comes
from a functor of Schur-Weyl type between their module categories.
From quantum loop algebras to Yangians pdf
: The main purpose of this note is to give a proof of a statement
of V. Drinfeld regarding Yangians and quantum loop algebras, namely how
the former can be constructed as limit forms of the latter. We also
apply the same ideas to twisted quantum loop algebras to recover the
(non-twisted) Yangians.
Twisted affine Lie superalgebra of type Q and quantization of its enveloping superalgebra pdf
: We introduce a new quantum group which is a
quantization of the enveloping superalgebra of a twisted affine Lie
superalgebra of type Q. We
study generators and relations for superalgebras in the finite and
twisted affine case, and also universal central extensions. Afterwards,
we apply the FRT formalism to a certain solution of the quantum
Yang-Baxter equation to define that new quantum group and we study some
of its properties. We construct a functor of Schur-Weyl type which
connects it to affine Hecke-Clifford algebras and prove that it provides
an equivalence between two categories of modules.
Central extensions of matrix Lie superalgebras over Z/2Z-graded algebras pdf
: We study central extensions of the Lie superalgebra sl_n(A) when A is a Z/2Z-graded superalgebra over a commutative ring K. Steinberg Lie superalgebras and their central extensions play an essential role. We use a Z/2Z-graded version of cyclic homology to study the center of the extensions in question.
Double
affine Lie algebras and finite groups pdf
: We begin to study
the Lie theoretical analogs of symplectic reflection algebras for a
finite cyclic group G, which
we call ``cyclic double affine Lie
algebra''. We focus on type A
: in the finite (resp. affine, double
affine) case, we prove that these structures are finite (resp. affine,
toroidal) type Lie algebras, but the gradings differ. The case which is
essentially new is the smash product of C[u,v] with G. We describe its
universal central extensions and start the study of its representation
theory, in particular of its highest weight integrable modules and Weyl
modules. We also consider the first Weyl algebra A_1 instead of the
polynomial ring C[u,v], and,
more generally, a rank one rational
Cherednik algebra. We study quasi-finite highest weight
representations of these Lie algebras.
Quantum
algebras and quivers pdf : This paper starts with some general results about Lie algebras of type A
over quadratic algebras and then
suggests a definition of deformed double current algebras for any
simple Lie algebra. To a quiver Q,
we associate a new family of
quantum algebras which are deformationZ/2Zs of the enveloping algebra of a
Lie algebra slightly larger than the universal central extension of sl_n defined over the preprojective
algebra of Q. We study some
of their structural properties, obtain a Schur-Weyl
functor connecting them to deformed preprojective algebras for wreath
products, prove that they have the PBW property when Q is an
affine Dynkin quiver and we relate them to the quantum algebras studied
in our previous paper. We are able to construct reflection functors
between categories of modules over our quantum quiver algebras for
different values of the deformation parameters.
Quantum
algebras and symplectic reflection algebras for wreath products pdf : We generalize the results of the two papers immediately below to the
case of symplectic reflection algebras for wreath products of finite
subgroups G of SL_2(C). We introduce a new family
of algebras called G-deformed
double current algebras (G-DDCAs)
and
construct for them Poincare-Birkhoff-Witt bases to show that they are
flat deformations of the enveloping algebra of an enlargement of the
universal central extension of sl_n
over the smash product of C[u,v]
with G.
When G is a cyclic group, we
are able to connect G-DDCAs
to Yangians.
Affine
Yangians and deformed double current algebras in type A pdf : We focus on the structure of the algebras in question. We construct
Poincare-Birkhoff-Witt bases for affine Yangians and deformed double
current algebras (DDCAs) using a module obtained by applying the
Schur-Weyl functor to a Cherednik algebra, we explain how to obtain
them via a limit procedure starting from quantum toroidal algebras, and
we show that they are deformations of matrix W1+oo-algebras.
We are also able to establish the equivalence of three different
definitions of DDCAs.
Cherednik
algebras and Yangians pdf
: We construct a functor F
from the category of modules over
a trigonometric
Cherednik algebra of type gl_l
to a certain category of
modules over an affine Yangian for sl_n.
This extends the
classical Schur-Weyl construction. We give a sufficient condition for
this functor to be an equivalence. Our main goal, which is achieved in
the second part, was to identify the Schur-Weyl dual of a rational
Cherednik algebra for the symmetric group S_l: the answer is given by
a new family of algebras that we have called deformed polynomial double
loop algebras (deformed double current algebras in the subsequent
papers).
On the
Category O for Rational
Cherednik Algebras pdf : This article
provides an exhaustive study of the category O of modules
over the rational Cherednik algebra Hk (associated to a finite
complex reflection group W)
and of the functor KZ from O to the category mod-H of finitely generated
modules over a finite Hecke algebra H. In the first
section, we
study the highest weight structure of the category O; many
results are valid over quite general base rings. The following two
sections introduce different duality functors between Cherednik
algebras, study homological properties of O and provide a
construction of the semi-regular bimodule of Hk.
The three main results of this paper concern the functor KZ:
- H
is isomorphic to EndH(PKZ)opp where PKZ
is a certain projective object in O.
- Double-centralizer theorem: The map HomH(M,Q) --->HomH(KZ(M),KZ(Q)) induced by the
functor KZ is an isomorphism
if M,Q are in O and Q is projective.
- If the parameter k is
just one positive real number and W
is
a Weyl group, then the image of a Verma module under KZ is isomorphic to the cell
(standard) module of H corresponding
to the same irreducible
representation of W as the
Verma module.
Projective
Modules in the Category O for
the Cherednik algebra pdf
: We study the category O of a
rational Cherednik algebra H.
The
first result is that O has
enough projective objects. Our
main theorem states that O is
a highest weight category
with duality; in particular, projective modules admit filtrations whose
successive subquotients are standard modules. This last property is
derived from a quite explicit construction of projectives in O. From our main result, it follows
that an analog of the
BGG-reciprocity formula, which connects projective, standard and simple
modules, holds in O.
Finally, we provide an upper
bound on the cohomological dimension of O.
Embeddings
of symmetric varieties pdf
: The construction of the enveloping semigroup of a semisimple algebraic group G, due to E.B. Vinberg, is
generalized to the case of a symmetric variety G/K, K being the
fixed-point subgroup of an involution of G. We construct a variety Env(G/K) which is an affine
spherical embedding of G/K.
We
use the language of colored cones and study some properties of this
enveloping variety. We recall a few facts about the wonderful
compactification of the adjoint Gad/Kad
due to C. De Concini and C. Procesi, and we establish
two connections between it and Env(G/K):
first, Env(G/K) is a fiber
product,
over an affine toric variety, of an affine space with the normalization
of a multi-cone over the compactification of Gad/Kad;
secondly, under a
certain assumption on G/K, we
realize this compactification as a
geometric quotient of an open subvariety of Env(G/K).
Office hours in CAB 665:
Wednesday 1-2pm, Friday 1-3pm, and by appointment.
Links:
University of Alberta
Mathematical and Statistical Sciences
e-print arXiv