Improper Integrals

Section 4.1 Improper Integrals

In this section, we extend the concept of a definite integral,

\int_{a}^{b} f (x) d x

$\int_a^b f(x) \ dx$ defined on a finite interval

[a, b],

$[a,b]\text{,}$ to the cases where either

the interval is infinite, or
the integrand approaches infinity at one or more points on the interval $[a,b]\text{.}$

🔗

In these cases, the resulting integrals are called improper integrals. We distinguish between

improper integrals of the first kind, where the interval of integration is infinite, and
improper integrals of the second kind, where the integrand approaches infinity at one or more points on the interval of integration.

🔗

Subsection 4.1.1 Motivational Example Leading to an Improper Integral of the First Kind

🔗

Suppose that a chemical is produced at a rate of

e^{- t}

$e^{-t}$ moles/second. At time

t = 0,

$t=0\text{,}$ this chemical is produced at a rate of 1 mole/second, after which the rate of production decreases exponentially.

🔗

The amount of chemical produced up to time

t = 3

$t=3$ seconds is represented by the definite integral

\begin{matrix} \int_{0}^{3} e^{- t} d t & = {(- e^{- t}) ∣ ∣}_{0}^{3} = - e^{- 3} - (- e^{0}) = - e^{- 3} + 1 = 1 - e^{- 3} \approx 0.95 moles . \end{matrix}

$\begin{alignat*}{1} \int_0^{3} e^{-t} \ dt &= \left. \left( - e^{-t} \right) \right|_0^{3} \\ &= -e^{-3} - \left( -e^{0} \right) \\ &= -e^{-3} + 1 = 1 - e^{-3} \approx 0.95 \ \mbox{moles}. \end{alignat*}$

🔗

What if the process runs forever? Will the amount of chemical produced be infinite? Or finite? If the amount is finite, how much? It seems that we need to evaluate the following improper integral of the first kind:

\int_{0}^{\infty} e^{- t} d t .

$\int_0^{\infty} e^{-t}\ dt.$ But how do we do that?

🔗

Subsection 4.1.2 Handling an Improper Integral of the First Kind

🔗

In the following video, we will show how to deal with an improper integral of the first kind that has the form

\int_{a}^{\infty} f (x) d x,

$\displaystyle \int_a^{\infty} f(x) \ dx\text{,}$ and work through a couple of examples, including the example introduced above.

🔗

Figure 4.1.1. Video demonstrating how to deal with an improper integral of the first kind where the upper limit of integration is

\infty .

$\infty\text{.}$

🔗

Integrals of the form

\int_{- \infty}^{a} f (x) d x

$\displaystyle \int_{-\infty}^a f(x) \ dx$ and

\int_{- \infty}^{\infty} f (x) d x

$\displaystyle \int_{-\infty}^{\infty} f(x) \ dx$ also are improper integrals of the first kind.

🔗

In the following video, we show how to deal with these improper integrals and work through a few additional examples.

🔗

Figure 4.1.2. Video demonstrating how to deal with an improper integral of the first kind where the lower limit of integration is

- \infty,

$-\infty\text{,}$ or where the lower limit of integration is

- \infty

$-\infty$ and the upper limit of integration is

\infty .

$\infty\text{.}$

🔗

Subsection 4.1.3 Handling an Improper Integral of the Second Kind

🔗

Recall that improper integrals of the second kind are those where the integrand approaches infinity at least once on the interval of integration. An example is

\int_{- 1}^{2} \frac{1}{x^{2}} d x .

$\displaystyle \int_{-1}^{2} \frac{1}{x^2} \ dx.$ Recall that the antiderivative of

1 / x^{2}

$1/x^2$ is

- 1 / x .

$-1/x\text{.}$ If we were to proceed carelessly, we might write the following:

\begin{matrix} \int_{- 1}^{2} \frac{1}{x^{2}} d x & = {(- \frac{1}{x}) ∣ ∣ ∣}_{- 1}^{2} = - \frac{1}{2} - (- \frac{1}{- 1}) = - \frac{1}{2} + \frac{1}{- 1} = - \frac{1}{2} - 1 = - \frac{3}{2} . \end{matrix}

$\begin{alignat*}{1} \int_{-1}^2 \frac{1}{x^2} \ dx &= \left. \left( - \frac{1}{x} \right) \right|_{-1}^2 \\ &= -\frac{1}{2} - \left( - \frac{1}{-1} \right) \\ &= -\frac{1}{2} + \frac{1}{-1} = -\frac{1}{2} - 1 = -\frac{3}{2}. \end{alignat*}$

🔗

We obtained a negative value. But surely this cannot be right, since the function

f (x) = \frac{1}{x^{2}}

$\displaystyle f(x) = \frac{1}{x^2}$ is a positive function (it lies entirely above the

$x$ -axis), as shown in the following graph:

🔗
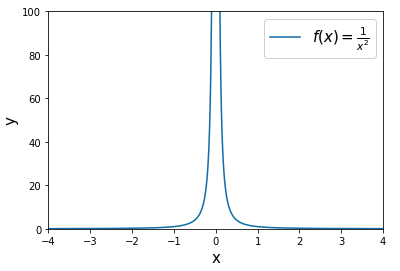
Figure Graph of the function $f(x) = 1/x^2$ which is undefined at $x=0\text{.}$

🔗

Since

$\displaystyle f(x) = \frac{1}{x^2}$ is a positive function, any definite integral must evaluate to a positive number.

🔗

The reason for the strange result (obtaining a negative number) lies in the fact that

$\displaystyle \int_{-1}^{2} \frac{1}{x^2} \ dx$ is not a definite integral, but an improper integral whose integrand is undefined at

$0\text{.}$

🔗

In the following video, we show how to handle improper integrals of the second kind, and work through a couple of examples, including the example introduced above.

🔗

Figure 4.1.4. Video demonstrating how to deal with an improper integral of the second kind.

🔗

Subsection 4.1.4 Summary

🔗

If an improper integral has an integrand for which we can find an antiderivative (through any method at our disposal), then we can introduce limits to take care of any improprieties, and carry the calculation of the improper integral to completion.
An improper integral is called convergent if the corresponding limit exists; otherwise it is called divergent.
Improper Integrals of the First Kind:
- For an improper integral of the first kind, the impropriety is at least one infinite limit of integration.
- If $\displaystyle \int_a^b f(x) \ dx$ exists for every number $b \ge a\text{,}$ then $\int_a^{\infty} f(x) \ dx = \lim_{b \to \infty} \int_a^b f(x) \ dx$ provided this limit exits (as a finite number).
- If $\displaystyle \int_a^b f(x) \ dx$ exists for every number $a \le b\text{,}$ then $\int_{-\infty}^{b} f(x) \ dx = \lim_{a \to -\infty} \int_a^b f(x) \ dx$ provided this limit exits (as a finite number).
- If both $\displaystyle \int_{-\infty}^c f(x) \ dx$ and $\displaystyle \int_c^{\infty} f(x) \ dx$ are convergent, then $\int_{-\infty}^{\infty} f(x) \ dx = \int_{-\infty}^c f(x) \ dx + \int_c^{\infty} f(x) \ dx$ where $c$ is any real number.
Improper Integrals of the Second Kind:
- For an improper integral of the second kind, the impropriety is the integrand that goes to infinity somewhere in the interval of integration.
- If $f$ is continuous on $[a,c)$ and is discontinuous at $c\text{,}$ then $\int_a^c f(x) \ dx = \lim_{b \to c^-} \int_a^b f(x) \ dx$ provided this limits exists (as a finite number).
- If $f$ is continuous on $(c,b]$ and is discontinuous at $c\text{,}$ then $\int_c^b f(x) \ dx = \lim_{a \to c^+} \int_a^b f(x) \ dx$ provided this limits exists (as a finite number).
- If $f$ has a discontinuity at $c\text{,}$ where $a \lt c \lt b\text{,}$ and both $\displaystyle \int_a^c f(x) \ dx$ and $\displaystyle \int_c^b f(x) \ dx$ are convergent, then $\int_a^b f(x) \ dx = \int_a^c f(x) \ dx + \int_c^b f(x) \ dx.$

🔗

Subsection 4.1.5 Don't Forget

🔗

Don't forget to return to eClass to complete the pre-class quiz.

🔗

Subsection 4.1.6 Further Study

🔗

Remember that the notes presented above only serve as an introduction to the topic. Further study of the topic will be required. This includes working through the pre-class quizzes, reviewing the lecture notes, and diligently working through the homework problems.

🔗

As you study, you should reflect on the following learning outcomes, and critically assess where you are on the path to achieving these learning outcomes:

🔗

Learning Outcomes

Recognize an integral with at least one infinite limit of integration as an improper integral of the First Kind, rewrite it as the limit of a definite integral, and evaluate the limit or determine that it diverges.
Recognize an integral with an integrand that is undefined on the interval of integration as an improper integral of the Second Kind, rewrite it as the limit of a definite integral, and evaluate the limit or determine that it diverges.

🔗

The following references provide a good start for review and further study:

Learning Outcome	Video	Textbook Section
1	4.E1, 4.E2	5.8
2	4.E3	N/A