Section 13.1 Maximum and Minimum Values
Subsection 13.1.1 Definitions: Local vs Absolute Maxima and Minima
Recall that a function of two variables, \(z=f(x,y)\text{,}\) defines a surface. An example of such surface, with local and absolute extrema indicated, is shown below.
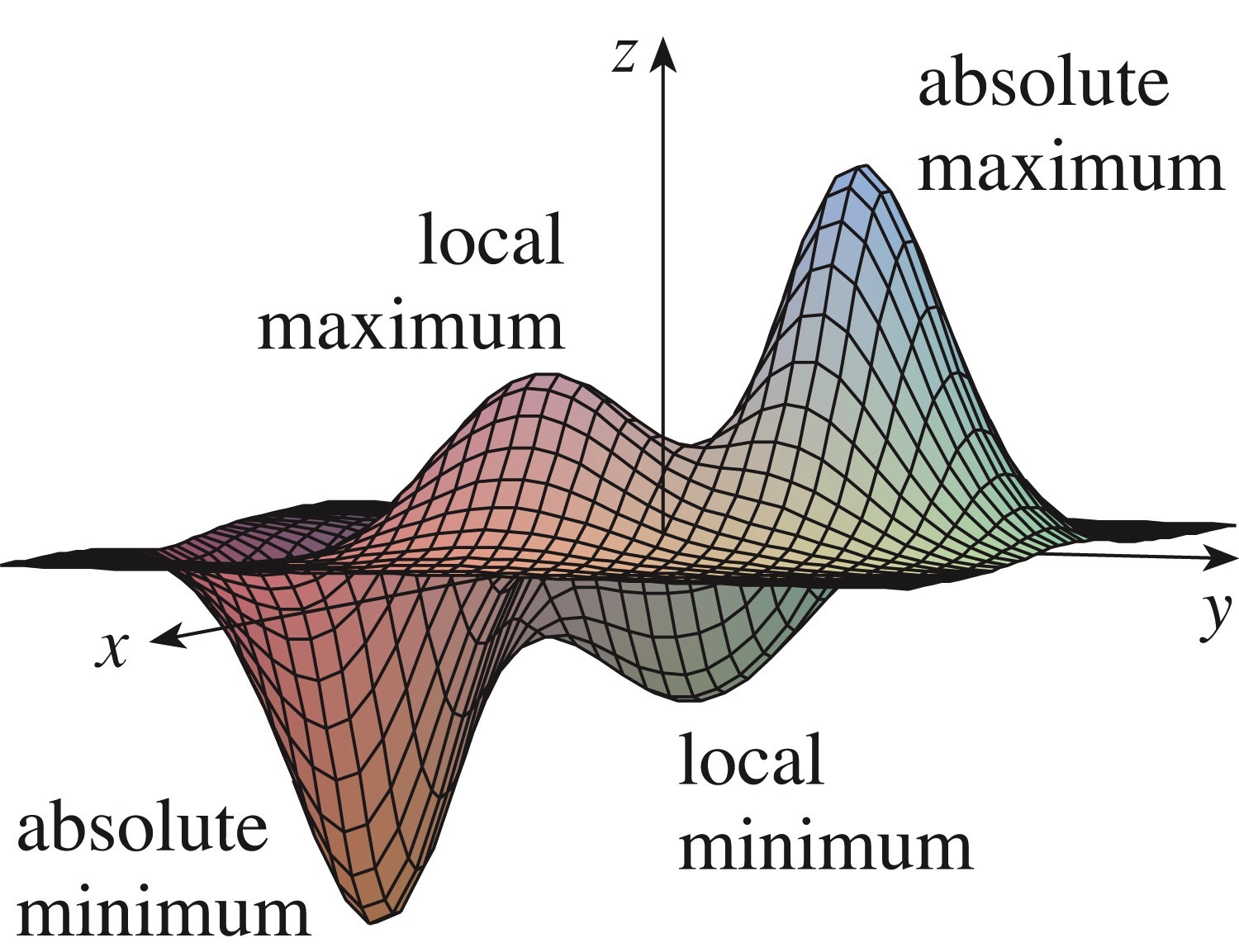
We define local and absolute extrema as follows:
Definition 13.1.2.
A function \(f(x,y)\) has a local maximum at \((a,b)\) if \(f(x,y) \le f(a,b)\) when \((x,y)\) is near \((a,b)\text{.}\) The number \((a,b)\) is called a local maximum value.Definition 13.1.3.
A function \(f(x,y)\) has a local minimum at \((a,b)\) if \(f(x,y) \ge f(a,b)\) when \((x,y)\) is near \((a,b)\text{.}\) The number \((a,b)\) is called a local minimum value.Definition 13.1.4.
If \(f(x,y) \le f(a,b)\) for all \((x,y)\) in the domain of \(f\text{,}\) then \(f\) has an absolute maximum value at \((a,b)\text{.}\)Definition 13.1.5.
If \(f(x,y) \ge f(a,b)\) for all \((x,y)\) in the domain of \(f\text{,}\) then \(f\) has an absolute minimum value at \((a,b)\text{.}\)Subsection 13.1.2 Characteristics of Local Extrema
Recall that a function of one variable, a local extremum may be found at \(c\) if \(f'(c) = 0\) (if there is a horizontal tangent line at \(c\)) or if \(f'(c)\) does not exist (if there is no tangent line, for example, at the vertex of the graph of \(y=|x|\)).
This idea carries over nicely to functions of two variables. Instead of tangent lines, we must consider tangent planes. The orientation of a tangent plane at \((a,b)\) is determined by the partial derivatives \(f_x(a,b)\) and \(f_y(a,b)\text{.}\) The tangent plane is horizontal (parallel to the \(xy\) plane) if both \(f_x(a,b)= 0\) and \(f_y(a,b)=0\text{.}\)
For a function of two variables then, a local extremum may be found at \((a,b)\) if both \(f_x(a,b)= 0\) and \(f_y(a,b)=0\) (if there is a horizontal tangent plane at \((a,b)\)) or if \(f_x(a,b)\) or \(f_y(a,b)\) does not exist (if there is no tangent plane at \((a,b)\)).
Examples of three surfaces with a local extremum at \((0,0)\) are shown below.
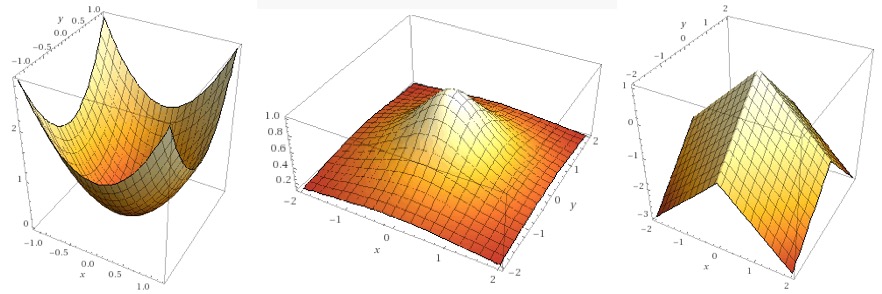
plot x^2+y^2, plot 1/(1+x^2+y^2) x=-2..2 y=-2..2, and plot 1-abs(x)-abs(y), respectively.For the first two examples, the surfaces are smooth at \((0,0)\text{,}\) that is, both \(f_x(0,0)\) and \(f_y(0,0)\) exist. Moreover, these partial derivatives are 0, and there is a horizontal tangent plane at \((0,0)\text{.}\) For the first example, there is a local minimum at \((0,0)\text{;}\) for the second example, there is a local maximum at \((0,0)\text{.}\)
For the third example, there is a local maximum at \((0,0)\text{.}\) However, the surface is not smooth there; it has a sharp vertex at \((0,0)\) and there is no tangent plane at \((0,0)\text{.}\) Neither \(f_x(0,0)\) nor \(f_y(0,0)\) exists.
Subsection 13.1.3 Critical Points
Recall that for a function of one variable, \(y=f(x)\text{,}\) a number \(c\) in the domain of \(f(x)\) is a critical number of \(f\) if \(f'(c)=0\) or \(f'(c)\) does not exist.
Similarly, for a function of two variables, \(z=f(x,y)\text{,}\) a point \((a,b)\) in the domain of \(f(x,y)\) is a critical point of \(f(x,y)\) if \(f_x(a,b)=0\) and \(f_y(a,b)=0\text{,}\) or if one (or both) of these partial derivatives does not exist.
Recall that for a function of one variable, we have to be careful not to make the conclusion that there is a local extremum at \(c\) if \(f'(c)=0\text{.}\) Instead, there may be a point of inflection. For example, think of \(c=0\) for \(f(x) = x^3\text{.}\)
Similarly for functions of two variables: we cannot make the conclusion that there is a local extremum at \((a,b)\) if both \(f_x(a,b)=0\) and \(f_y(a,b)=0\text{.}\) Instead, there may be a saddle point, such as illustrated in the following figure, showing the surface \(f(x,y) = x^2 - y^2\text{.}\)
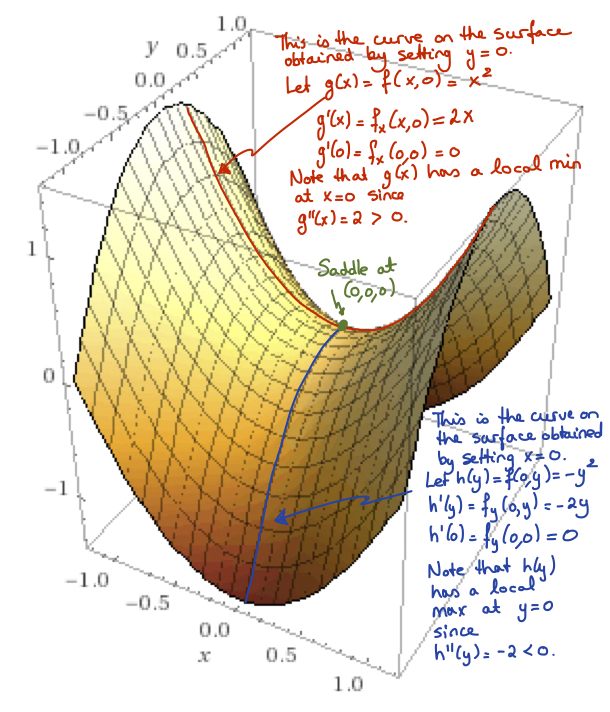
plot x^2-y^2.Note that \(f_x = 2x = 0\) when \(x=0\) and \(f_y = -2y = 0\) when \(y=0\text{.}\) That is, \((0,0)\) is a critical point. However, there is no local extremum at \((0,0)\text{,}\) but a saddle point (if you stand at the saddle point, you see the surface decreasing in the direction of positive and negative \(y\) and increasing in the direction of positive and negative \(x\)).
In the following video, we work through the details of finding all critical points for the function \(f(x,y) = xy(x-2)(y+3)\text{.}\)
Subsection 13.1.4 Characterizing Critical Points
The Second Derivatives Test for functions of two variables is analogous to the Second Derivative Test for functions of one variable. We state it here without proof or justification (this is beyond the scope of this course)
Suppose that the second partial derivatives of \(f(x,y)\) are continuous on a disk centered at the point \((a,b)\text{,}\) where \(f_x(a,b) = 0\) and \(f_y(a,b) = 0\text{.}\) Let $$ D(x,y) = f_{xx} f_{yy} - f_{xy}^2. $$
- If \(D(a,b) \gt 0\) and \(f_{xx}(a,b) \lt 0\text{,}\) then \(f(a,b)\) is a local maximum.
- If \(D(a,b) \gt 0\) and \(f_{xx}(a,b) \gt 0\text{,}\) then \(f(a,b)\) is a local minimum.
- If \(D(a,b) \lt 0\text{,}\) then \(f\) has a saddle point at \((a,b)\text{.}\)
- If \(D(a,b) = 0\text{,}\) then the test is inconclusive: \(f\) could have a local maximum or minimum at \((a,b)\text{,}\) or \((a,b)\) could be a saddle point of \(f\text{.}\)
In the following video, we characterize all critical points for the surface given \(z = f(x,y) = xy(x-2)(y+3)\text{.}\)
Subsection 13.1.5 Finding Absolute Absolute Maximum and Minimum Values
For functions of one variable, the existence of absolute extrema is guaranteed on a closed interval. To find the absolute extrema, we can use the Closed Interval Method, which instructs us to evaluate the function at all critical points and at the endpoints of the interval, and then select the largest and smallest functions values.
The Closed Interval Method naturally extends to functions of two variables. Instead of a working on a closed interval, we need to work on a closed, bounded set (a closed set in \(\mathbb{R}^2\) is a set that includes its boundary; a bounded set is one that can be contained within a disk of finite radius). An example of a closed, bounded set is the rectangle defined by all \((x,y)\) such that \(0 \le x \le 3\) and \(0 \le y \le 2\text{.}\)
To find the absolute maximum and minimum values of a continuous function \(f(x,y)\) on a closed, bounded set \(D\) in \(\mathbb{R}^2\text{:}\)
- Determine the critical points of \(f\) in the interior of \(D\text{.}\)
- Determine candidate points for extreme values of \(f\) on the boundary of \(D\) (critical points on the boundary and/or end points).
- Determine the values of \(f\) at all critical points in the interior of \(D\) and all candidate points on the boundary of \(D\text{.}\)
- The largest of the values from step 3 is the absolute maximum; the smallest of these values is the absolute minimum.
In the following video, we work through the details of determining the absolute extrema of the function \(f(x,y) = 4 + 2x^2 + y^2\) on the rectangle \(R = \{ (x,y) | -1 \le x \le 1, -1 \le y \le 1 \}\text{.}\)
Subsection 13.1.6 Summary
Local Maximum and Minimum Values.
- A function \(f(x,y)\) has a local maximum at \((a,b)\) if \(f(x,y) \le f(a,b)\) when \((x,y)\) is near \((a,b)\text{.}\) The number \((a,b)\) is called a local maximum value.
- A function \(f(x,y)\) has a local minimum at \((a,b)\) if \(f(x,y) \ge f(a,b)\) when \((x,y)\) is near \((a,b)\text{.}\) The number \((a,b)\) is called a local minimum value.
Absolute Maximum and Minimum Values.
- If \(f(x,y) \le f(a,b)\) for all \((x,y)\) in the domain of \(f\text{,}\) then \(f\) has an absolute maximum value at \((a,b)\text{.}\)
- If \(f(x,y) \ge f(a,b)\) for all \((x,y)\) in the domain of \(f\text{,}\) then \(f\) has an absolute minimum value at \((a,b)\text{.}\)
Critical Points.
-
An interior point \((a,b)\) in the domain of \(f(x,y)\) is called a critical point of \(f(x,y)\) if \(f_x(a,b)=0\) and \(f_y(a,b)=0\text{,}\) or if one (or both) of these partial derivatives does not exist.
- If \(f(x,y)\) has a local maximum or minimum at \((a,b)\text{,}\) then \((a,b)\) is a critical point of \(f\text{.}\)
- Critical points are candidates for local maximum and minimum values; if \((a,b)\) is a critical point of \(f(x,y)\text{,}\) there may or may not be a local maximum or local minimum at \((a,b)\text{.}\)
Second Derivatives Test.
-
Suppose that the second partial derivatives of \(f(x,y)\) are continuous on a disk centered at the point \((a,b)\text{,}\) where \(f_x(a,b) = 0\) and \(f_y(a,b) = 0\text{.}\) Let $$ D(x,y) = f_{xx} f_{yy} - f_{xy}^2. $$
- If \(D(a,b) \gt 0\) and \(f_{xx}(a,b) \lt 0\text{,}\) then \(f(a,b)\) is a local maximum.
- If \(D(a,b) \gt 0\) and \(f_{xx}(a,b) \gt 0\text{,}\) then \(f(a,b)\) is a local minimum.
- If \(D(a,b) \lt 0\text{,}\) then \(f\) has a saddle point at \((a,b)\text{.}\)
- If \(D(a,b) = 0\text{,}\) then the test is inconclusive: \(f\) could have a local maximum or minimum at \((a,b)\text{,}\) or \((a,b)\) could be a saddle point of \(f\text{.}\)
Finding Absolute Maximum and Minimum Values.
-
To find the absolute maximum and minimum values of a continuous function \(f(x,y)\) on a closed, bounded set \(D\) in \(\mathbb{R}^2\text{:}\)
- Determine the critical points of \(f\) in the interior of \(D\text{.}\)
- Determine candidate points for extreme values of \(f\) on the boundary of \(D\) (critical points on the boundary and/or end points).
- Determine the values of \(f\) at all critical points in the interior of \(D\) and all candidate points on the boundary of \(D\text{.}\)
- The largest of the values from step 3 is the absolute maximum; the smallest of these values is the absolute minimum.
Subsection 13.1.7 Don't Forget
Don't forget to return to eClass to complete the pre-class quiz.
Subsection 13.1.8 Further Study
Remember that the notes presented above only serve as an introduction to the topic. Further study of the topic will be required. This includes working through the pre-class quizzes, reviewing the lecture notes, and diligently working through the homework problems.
As you study, you should reflect on the following learning outcomes, and critically assess where you are on the path to achieving these learning outcomes:
Learning Outcomes
- Recall the definition for local and absolute extrema of a function of two variables.
- Find all critical points for a given function of two variables.
- Use the Second Derivatives Test to characterize a critical point as a local minimum, a local maximum, or a saddle point, or to conclude that the test is inconclusive.
- Determine the absolute extrema for a given continuous function of two variables on a closed, bounded set \(D\text{,}\) where \(D\) is a rectangle, triangle, or circle.
- Convert a given word problem into a mathematical optimization problem by setting up the function for a quantity that is to be maximized or minimized, and apply optimization techniques to solve the word problem.
The following references provide a good start for review and further study:
| Learning Outcome | Video | Textbook Section |
|---|---|---|
| 1 | N/A | 9.6 |
| 2 | 13.E1 | 9.6 |
| 3 | 13.E2 | 9.6 |
| 4 | 13.E3 | 9.6 |
| 5 | N/A | 9.6 |