Section 6.1 Volumes of Solids of Revolution
Subsection 6.1.1 What is a Solid of Revolution?
A solid of revolution is a symmetric object, obtained by revolving (rotating) a region in the plane around a straight line in the plane (assuming that this line does not intersect the region).
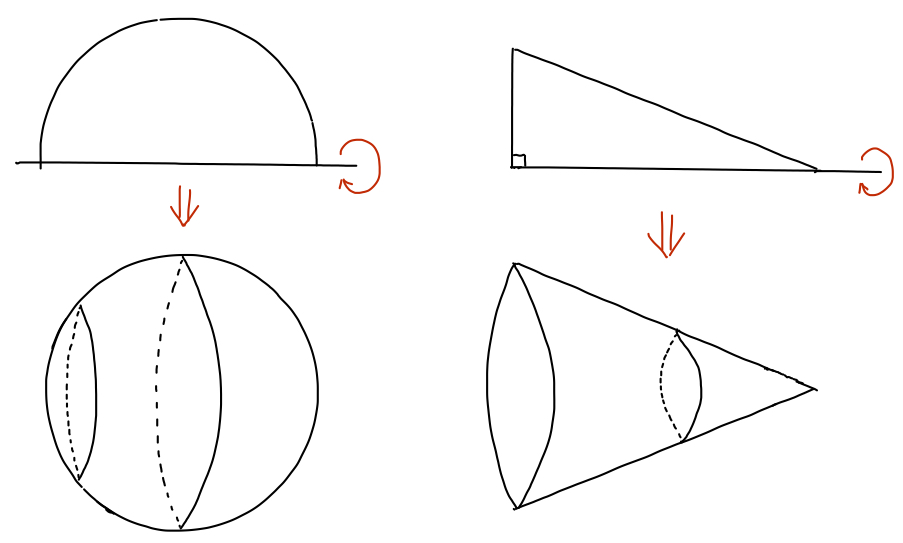
For example, the unit sphere can be understood to be the result of revolving the upper half of the unit circle around the \(x\)-axis. Similarly, the right triangular cone can be understood to be the result of revolving a right triangle about either one of the sides that is not the hypotenuse, as illustrated below.
The following animation nicely demonstrates the result of revolving a curve around a vertical line resulting in a surface of revolution. The surface of revolution encloses a solid of revolution.
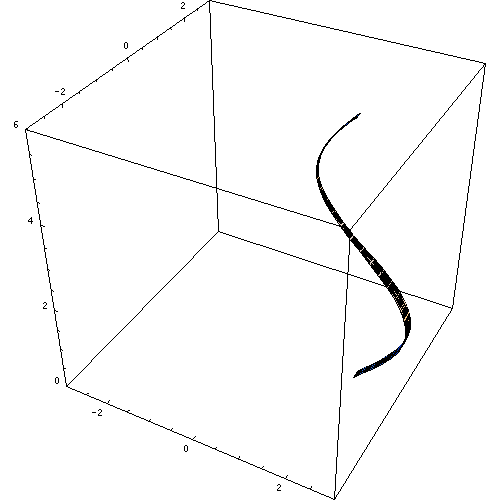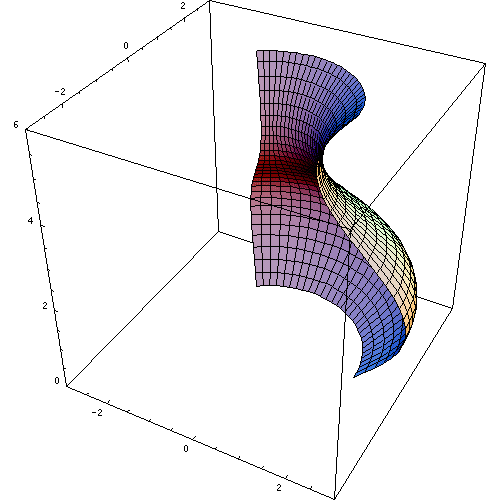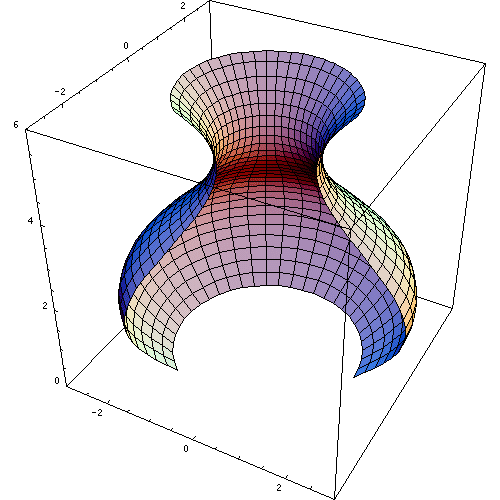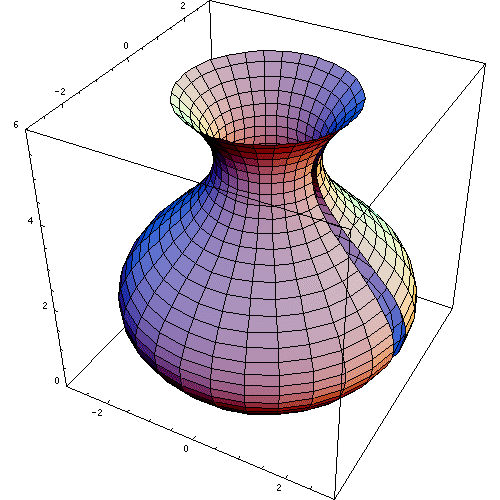
Subsection 6.1.2 Slicing a Solid of Revolution to Determine Its Volume
In this course, we restrict ourselves to the case where a planar region is revolved around a horizontal line.
The general approach to determine the volume of the resulting solid of revolution is as follows:
- We focus on a typical slice of the planar region, of infinitesimal thickness \(dx\text{.}\)
- We revolve the typical slice around the given axis of revolution.
- The typical slice generates either a solid disk, or a washer (a disk with a hole).
- We determine the cross-sectional area of the disk or washer, \(A(x)\text{.}\)
- We determine the volume of the disk or washer, \(dV = A(x) dx\text{.}\)
- We integrate to obtain the volume of the entire object, $$V = \int dV = \int_a^b A(x) \ dx.$$
Subsection 6.1.3 Solids of Revolution with Slices that are Disks
Both the sphere and the right triangular cone are solids of revolution where the cross-sections are circles, so that we can view the infinitesimally thin slices as disks.
In the following video, we will use the approach outlined above to determine the volume of a sphere with radius \(R\text{.}\) We have known since kindergarten (give or take a few years!) that the volume of a sphere with radius \(R\) is $$ V_{sphere} = \frac{4}{3} \pi R^3. $$ With the calculus tools that we now have at hand, we finally can prove the origin of this formula. This is pretty powerful stuff!
Subsection 6.1.4 Solids of Revolution with Slices that are Washers
In many cases, the cross-sections of a solid of revolution are circles with holes, so that we can view the infinitesimally thin slices as washers (disks with holes).
In the following video, we demonstrate how the disk method from the previous example can be modified to account for the hole.
Remember to subtract the area of the hole from the area of the solid disk, resulting in $$ A = \pi \left( R_{outer}^2 - R_{inner}^2 \right). $$
Warning 6.1.5.
A very common mistake made by students is to write $$ A = \pi \left( R_{outer} - R_{inner} \right)^2, $$ which definitely is not the same (check it by multiplying out the latter)!Subsection 6.1.5 Summary
- The volume of a solid of revolution obtained by revolving a region in the plane between \(x=a\) and \(x=b\) around a horizontal axis is $$ V = \int dV = \int_a^b A(x) \ dx, $$ where \(A(x)\) is the cross-sectional area of a disk or a washer.
- The cross-sectional area of a disk with radius \(R(x)\) is $$ A(x) = \pi R^2(x). $$
- The cross-sectional area of a washer with outer radius \(R_{outer}(x)\) and inner radius (radius of the hole) \(R_{inner}(x)\) is $$ A(x) = \pi \left( R_{outer}^2(x) - R_{inner}^2(x) \right). $$
Subsection 6.1.6 Don't Forget
Don't forget to return to eClass to complete the pre-class quiz.
Subsection 6.1.7 Further Study
Remember that the notes presented above only serve as an introduction to the topic. Further study of the topic will be required. This includes working through the pre-class quizzes, reviewing the lecture notes, and diligently working through the homework problems.
As you study, you should reflect on the following learning outcomes, and critically assess where you are on the path to achieving these learning outcomes:
Learning Outcomes
- Set up the definite integral that represents the volume of a solid of revolution using the disk method.
- Set up the definite integral that represents the volume of a solid of revolution using the washer method.
The following references provide a good start for review and further study:
| Learning Outcome | Video | Textbook Section |
|---|---|---|
| 1 | 6.E1 | 6.4 (Examples 2 and 3 |
| 2 | 6.E2 | 6.4 (Example 4) |