Skip to main content

Section 3.2 L'Hospital's Rule

In this section, we return to the study of limits.

Subsection 3.2.1 Previous Encounters with Limits

We have come across limits previously in two different contexts, namely in the definition of the derivative, and in determining the behaviour of sequences and functions at infinity.

Subsubsection 3.2.1.1 Limits in the Definition of the Derivative

Recall that the derivative of a function \(f\) at \(x\) was defined as $$f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}$$ provided that this limit exists. Without knowing the rules of differentiation, determining the derivative \(f'(x)\) for a given \(f(x)\) is not obvious on first glance, since both the numerator and denominator approach \(0\) and \(\displaystyle \frac{0}{0}\) is not defined. When we encountered this type of limit in the past, we were able to evaluate it after simplifying the difference quotient through algebraic manipulation.

For \(\displaystyle f(x) = x^2\text{,}\) we have

\begin{alignat*}{1} f'(x) &= \lim_{h \to 0} \frac{ (x+h)^2 - x^2 }{h} \\ &= \lim_{h \to 0} \frac{ (x^2 + 2 x h + h^2) - x^2 }{ h } \\ &= \lim_{h \to 0} \frac{ 2xh + h^2 }{h} \\ &= \lim_{h \to 0} \frac{ h (2x + h ) }{h} \\ &= \lim_{h \to 0} \ (2x + h) \\ &= 2x. \end{alignat*}

The first four limits on the right-hand side are all of the type \(\displaystyle \frac{0}{0}\text{.}\) By algebraic manipulation, we see that we can divide both the numerator and denominator by \(h\text{,}\) after which we can finally evaluate the limit, and see that for \(f(x) = x^2\text{,}\) we have \(f'(x) = 2x\text{.}\)

Subsubsection 3.2.1.2 Limits at Infinity to Determine the Behaviour of a Function at Infinity

In determining the shape or graph of a function \(f(x)\text{,}\) it often is helpful to know how the function behaves for large values of \(x\text{.}\)

Consider the absorption function $$\alpha(c) = \frac{4c}{1+c},$$ where \(c\) is the concentration.

Remark 3.2.3.
An absorption function \(\alpha(c)\) describes the total amount of chemical absorbed as a function of the concentration \(c\text{.}\)

Both the numerator and denominator increase to infinity as \(c \to \infty\text{,}\) and so here we have a limit of the type \(\displaystyle \frac{\infty}{\infty}\text{.}\) With algebraic manipulation (namely dividing numerator and denominator by the highest power of \(c\) that occurs in the denominator), we can evaluate this limit as follows:

\begin{alignat*}{1} \lim_{c \to \infty} \frac{4c}{1+c} &= \lim_{c \to \infty} \frac{\frac{4c}{c}}{\frac{1}{c}+\frac{c}{c}} \\ &= \lim_{c \to \infty} \frac{ 4 }{ \frac{1}{c} + 1 } \\ &= \frac{ 4 }{ \lim_{c \to \infty} \frac{1}{c} + 1 } \\ &= \frac{ 4 }{ 0 + 1 } \\ &= 4. \end{alignat*}

We can conclude that the function \(\alpha(c)\) has a horizontal asymptote at 4, that is, absorption saturates at 4, as shown in the following graph: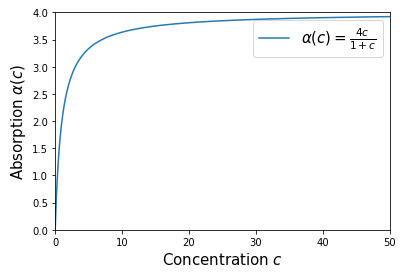

Figure 3.2.4. Graph of the absorption function \(\displaystyle \alpha(c) = \frac{4c}{1+c}\text{.}\)

Subsection 3.2.2 Some Problematic Limits

There are many instances where algebraic manipulations are of no help to determine a limit of the type \(\displaystyle \frac{0}{0}\) or of the type \(\displaystyle \frac{\infty}{\infty}\text{.}\) We refer to these limits as indeterminate form of type \(\displaystyle \frac{0}{0}\) and indeterminate form of type \(\displaystyle \frac{\infty}{\infty}\text{,}\) respectively. This is especially the case when trigonometric, exponential, and/or logarithmic functions are involved.

$$\lim_{x \to 0} \frac{e^x - 1}{x}$$ has indeterminate form of type\(\displaystyle \frac{0}{0}\) because both the numerator and denominator approach 0 as \(x \to 0\text{.}\)
$$\lim_{x \to \infty} \frac{ \ln(x) }{ x }$$ has indeterminate form of type\(\displaystyle \frac{\infty}{\infty}\) because both the numerator and denominator go to infinity as \(x \to \infty\text{.}\)

Neither limit can be evaluated with the methods that we have studied to date.

Subsection 3.2.3 L'Hospital's Rule to the Rescue

In the following video, we introduce a method, called L'Hospital's Rule, to determine limits that have indeterminate form of the type \(\displaystyle \frac{0}{0}\) or \(\displaystyle \frac{\infty}{\infty}\text{.}\) We will also give an intuitive rationale for why l'Hospital's Rule works and work through a few examples.

Figure 3.2.7. Video that introduces L'Hospital's Rule.

Subsection 3.2.4 More Problematic Limits

In addition to limits that have indeterminate forms of the type \(\displaystyle \frac{0}{0}\) or \(\displaystyle \frac{\infty}{\infty}\text{,}\) there are five other indeterminate forms, namely

  • type \(0 \cdot \infty\) (indeterminate product);
  • type \(\infty - \infty\) (indeterminate difference);
  • types \(0^0\text{,}\) \(\infty^0\text{,}\) and \(1^{\infty}\) (indeterminate powers).

With algebraic manipulations, each of these forms can be rewritten as an indeterminate form of the type \(\displaystyle \frac{0}{0}\) or \(\displaystyle \frac{\infty}{\infty}\text{,}\) after which l'Hospital's Rule can be applied. In the following video, we work through a few examples of this.

Figure 3.2.8. Video that illustrates how L'Hospital's Rule can be used to determine indeterminate products, differences, and powers.

Subsection 3.2.5 Summary

  • Suppose \(f\) and \(g\) are differentiable functions, and \(g'(x) \ne 0\) near \(a\) (except possibly at \(a\)). Further, suppose that $$ \lim_{x \to a} f(x) = 0 \ \ \ \mbox{and} \ \ \ \lim_{x \to a} g(x) = 0 $$ or $$ \lim_{x \to a} f(x) = \pm \infty \ \ \ \mbox{and} \ \ \ \lim_{x \to a} g(x) = \pm \infty. $$ With other words, we have an indeterminate form of type \(\displaystyle \frac{0}{0}\) or \(\displaystyle \frac{\infty}{\infty}\text{.}\)

    Then $$ \lim_{x \to a} \frac{ f(x) }{ g(x) } = \lim_{x \to a} \frac{ f'(x) }{ g'(x) }.$$

  • You should be able to recognize seven different types of indeterminate forms:

    • Indeterminate quotients have the form \(\displaystyle \frac{0}{0}\) and \(\displaystyle \frac{\infty}{\infty}\text{.}\)
    • Indeterminate products have the form \(0 \cdot \infty\text{.}\)
    • Indeterminate differences have the form \(\infty - \infty\text{.}\)
    • Indeterminate powers have the form \(0^0\text{,}\) \(\infty^0\text{,}\) and \(1^{\infty}\text{.}\)

  • Remember that:

    • L'Hospital's Rule directly apply ONLY to indeterminate quotients (\(\displaystyle \frac{0}{0}\) and \(\displaystyle \frac{\infty}{\infty}\)).
    • In the case of an indeterminate product (\(0 \cdot \infty\)) or indeterminate difference (\(\infty - \infty\)), first use algebraic manipulation to rewrite the indeterminate form as an indeterminate fraction, and then apply l'Hospital's Rule.
    • In the case of an indeterminate power (\(0^0\text{,}\) \(\infty^0\text{,}\) or \(1^{\infty}\)), first rewrite the limit via \(\displaystyle A = e^{\ln(A)}\text{,}\) then interchange the exponential function and the limit so that you can apply the limit to \(\ln(A)\text{,}\) and then use the laws of logarithms to simplify \(\ln(A)\) (resulting in the limit of an indeterminate product).

Subsection 3.2.6 Don't Forget

Don't forget to return to eClass to complete the pre-class quiz.

Subsection 3.2.7 Further Study

Remember that the notes presented above only serve as an introduction to the topic. Further study of the topic will be required. This includes working through the pre-class quizzes, reviewing the lecture notes, and diligently working through the homework problems.

As you study, you should reflect on the following learning outcomes, and critically assess where you are on the path to achieving these learning outcomes:

The following references provide a good start for review and further study:

Learning Outcome Video Textbook Section
1 3.E4, 3.E5 4.3
2 3.E4 4.3 (Examples 1-5)
3 3.E5 4.3 (Examples 8-11)
4 3.E5 N/A