Skip to main content

Section 3.1 Numerical Integration

In this section, we concern ourselves with the evaluation of a definite integral, \(\displaystyle \int_a^b f(x) \ dx\text{.}\)

Subsection 3.1.1 Evaluating a Definite Integral with the Evaluation Theorem

Provided that we can find an antiderivative of \(f(x)\text{,}\) then by the Evaluation Theorem, $$ \int_a^b f(x) \ dx = F(b) - F(a), $$ where \(F(x)\) is an antiderivative of \(f(x)\text{.}\)

Evaluate \(\displaystyle \int_2^5 x^2 \ dx\text{.}\)
Answer
\(\displaystyle \displaystyle \int_2^5 x^2 \ dx = \frac{117}{3}.\)
Solution
$$ \int_2^5 x^2 \ dx = \left. \frac{x^3}{3} \right|_2^5 = \frac{5^3}{3} - \frac{2^3}{3} = \frac{125-8}{3} = \frac{117}{3}.$$

Subsection 3.1.2 Two Situations when the Evaluation Theorem Cannot Be Used

There are two situations when the Evaluation Theorem cannot be used:

  1. When \(f(x)\) does not have an antiderivative that can be written in terms of elementary functions, or you cannot find the antiderivative because it requires an integration method that you do not (yet) know.

    The function \(f(x) = \sin(x^2)\) does not have an antiderivative that can be written in terms of elementary functions. We therefore cannot evaluate the definite integral $$ \int_0^3 \sin(x^2) \ dx$$ using the Evaluation Theorem. Note that Wolfram Alpha is able to provide an approximate value for the definite integral. Try it! It does this with a numerical integration method not unlike the ones that we learn about in this section.

  2. When we do not have an expression for \(f(x)\text{.}\)

    Consider the following data:

    Date Deaths/day
    March 1 0.0079
    March 15 0.0638
    March 29 0.1944
    April 12 0.4435
    April 26 0.5620
    May 10 0.4630
    May 24 0.2897

    This table shows the number of people who died from SARS in Singapore at two-week intervals beginning March 1, 2003. Integrating the (unknown) function of deaths/day as a function of time from March 1 to May 24 gives the total number of people who died from SARS during this period. If we let \(r(t)\) be the death rate (in deaths/day) and \(t\) be time (in days), then $$\int_0^{84} r(t) \ dt$$ represents the number of deaths during the 84-day period from March 1 to May 24.

For both of these situations, we can approximate (that is, calculate an estimate of) the value of the definite integral. To do so, it will be beneficial to recall the definition of the definite integral in terms of the limit of a Riemann sum.

Subsection 3.1.3 Review from Calculus I: Definition of the Definite Integral

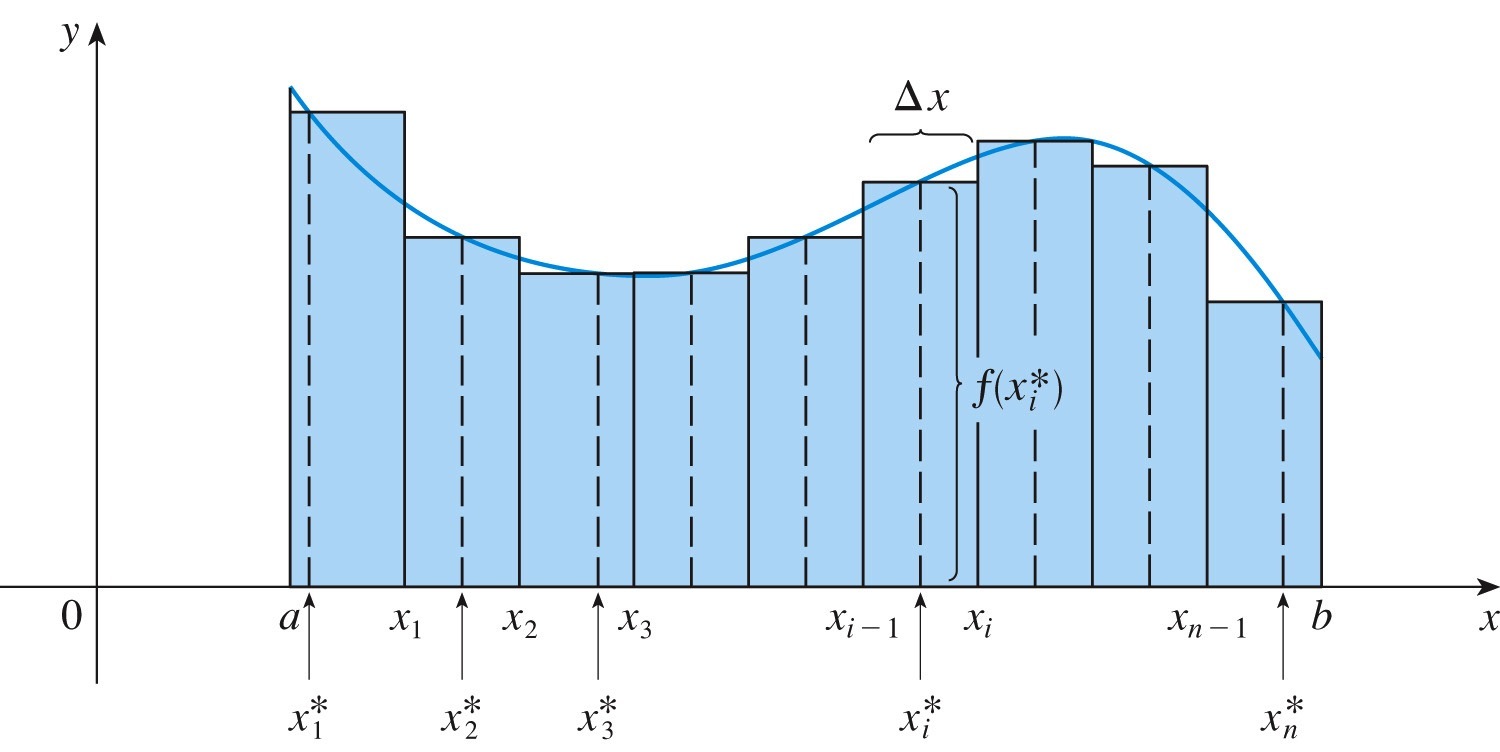
Figure 3.1.4. Approximating rectangles when the sample points \(x_i^*\) are not chosen to be endpoints. Source: Biocalculus: Calculus for the Life Sciences, James Stewart and Troy Day, Cengage Learning, 2015.

If a function is defined for \(a \le x \le b\text{,}\) we divide the interval \([a,b]\) into \(n\) subintervals of equal width \(\Delta x = \frac{b-a}{n}\text{.}\) We let \(x_0 (=a)\text{,}\) \(x_1\text{,}\) \(x_2\text{,}\) ..., \(x_n (=b)\) be the endpoints of these subintervals and we let \(x_1^*\text{,}\) \(x_2^*\text{,}\) ..., \(x_n^*\) be any sample points in these subintervals, so \(x_i^*\) lies in the \(i\)th subinterval \([x_{i-1}, x_i]\text{.}\) Then the definite integral of \(f\) from \(a\) to \(b\) is $$ \int_a^b f(x) \ dx = \lim_{n \to \infty} \sum_{i=1}^n f(x_i^*) \Delta x$$ provided that this limit exists.

Recall that the Riemann sum \(\displaystyle \sum_{i=1}^n f(x_i^*) \Delta x\) represents the area of the rectangles shown in the figure. The width of every rectangle is \(\Delta x\text{,}\) and the height of the \(i\)th rectangle is \(f(x_i^*)\text{.}\)

If you wish a refresher on the use of a limit of a Riemann sum to evaluate a definite integral, you may find it helpful to review the following video (from a first course on calculus such as MATH 114 or 134).

Figure 3.1.5. A video with an example of a limit of a Riemann sum to evaluate a definite integral.

Subsection 3.1.4 Omitting the Limit Leads to Approximation Methods

You likely remember that an exact evaluation of a definite integral using the Riemann sum is a formidable undertaking. That is because it is necessary to determine the Riemann sum first in terms of \(n\) only before being able to evaluate the limit as \(n\) goes to infinity.

Luckily, none of this is necessary when we approximate the integral! In that case, we omit the limit, and choose a 'small' (relative to an infinitely large) value for \(n\text{.}\)

Subsection 3.1.5 Right Point Rule and Left Point Rule

In the following video, we show how omitting the limit readily leads to two numerical integration methods, namely the Right Point Rule and the Left Point Rule, how those methods can be used to approximate the value of the definite integral introduced in Example 3.1.3.

Figure 3.1.6. Video demonstrating the use of the Right and Left Point Rules.

Subsection 3.1.6 Trapezoid Rule

As was mentioned in the video, neither the Right Point Rule nor the Left Point Rule are ideal, because each omits an important data point. The Right Point Rule does not make use of the first data point, and the Left Point Rule does not make use of the last data point.

In the following video, we introduce a new numerical method of integration, known as the Trapezoid Rule, that addresses this shortcoming, and obtain an improved approximation of the value of the definite integral in Example 3.1.3. We also demonstrate how to obtain an approximation of the definite integral in Example 3.1.2.

Figure 3.1.7. Video demonstrating the use of the Trapezoid Rule.

In general, we expect the Trapezoid Rule to give more accurate approximations than the Right Point Rule of the Left Point Rule. There are more sophisticated numerical integration schemes that give even better approximations, but they come at a computational cost. The Trapezoid Rule is a trusty, low-cost integrator that is suitable for many daily scientific applications.

Subsection 3.1.7 The Larger the Value of \(n\text{,}\) the Better the Approximation

Of course, we expect any of the numerical integration schemes to give more accurate approximations as \(n\) increases. For Example 3.1.3, \(n\) is limited by the number of data points we have available. But when we know the function to be integrated, such as in Example 3.1.2, we are free to choose the value of \(n\text{.}\)

In the following video, we introduce you to an app (developed by our colleague Dr. Jamie Mulholland from Simon Fraser University) where you see how computational power can be harnessed when wanting to use the Right Point Rule, the Left Point Rule, or the Trapezoid Rule to approximate the value of a definite integral for a known function.

Figure 3.1.8. Video demonstrating how to use Dr. Mulholland's app.

To experiment with Dr. Mulholland's app yourself, navigate to https://www.geogebra.org/m/v75ByEJ6.

Use Dr. Mulholland's app to approximate \(\displaystyle \int_0^1 \frac{4}{1+x^2} \ dx\) using the Trapezoid Rule for increasing values of \(n\text{,}\) and compare it to the actual value
\begin{alignat*}{1} \int_0^1 \frac{4}{1+x^2} \ dx &= \left. 4 \tan^{-1}(x) \right|_0^1 \\ &= 4 \left( \tan^{-1}(1) - \tan^{-1}(0) \right) \\ &= 4 \left( \frac{\pi}{4} - 0 \right) \\ &= \pi \\ &\approx 3.141592653\ldots \end{alignat*}
What do you notice?
Solution
  1. As \(n\) increases, the value of the approximation gets closer to the actual value of the integral.
  2. As \(n\) increases, more and more digits of the approximation remain fixed; only the last few digits in the approximation change.

Subsection 3.1.8 One Question Left Unanswered

For scientific applications, it may be necessary to approximate a given integral with a certain accuracy. For example, it may be necessary to know the value of \(\displaystyle \int_1^3 \sin(x^2) \ dx\) with an error that is less than \(\displaystyle 10^{-6}\) or with an accuracy of 4 decimal digits.

An important question of interest is: how do we choose which value of \(n\) to use to obtain the desired approximation accuracy?

We will discuss this question in class.

Subsection 3.1.9 Summary

Review of the Definition of the Definite Integral.
  • If \(f\) is a function defined for \(a \le x \le b\text{,}\) we divide the interval \([a, b]\) into \(n\) subintervals of equal width \(\Delta x = (b-a)/n\text{.}\) We let \(x_i = a + i \Delta x\) for \(i=0, 1, \ldots, n\) be the endpoints of these subintervals, and we let \(x_i^*\) be any sample points in these subintervals, so \(x_i^* \in [ x_{i-1}, x_i ]\text{.}\) Then the definite integral of \(f\) from \(a\) to \(b\) is $$ \int_a^b f(x) \ dx = \lim_{n \to \infty} \left( \sum_{i=1}^n f(x_i^*) \cdot \Delta x \right), $$ provided that this limit exists.
Approximations of the Definite Integral.

  • Right Point Rule: $$ \int_a^b f(x) \ dx \approx R_n = \Delta x \left[ y_1 + y_2 + \ldots + y_{n-1} + y_n \right] $$

  • Left Point Rule: $$ \int_a^b f(x) \ dx \approx L_n = \Delta x \left[ y_0 + y_1 + \ldots + y_{n-2} + y_{n-1} \right] $$

  • Trapezoid Rule: $$ \int_a^b f(x) \ dx \approx T_n = \frac{ \Delta x}{2} \left[ y_0 + 2 y_1 + 2 y_2 + \ldots + 2 y_{n-2} + 2 y_{n-1} + y_n \right] $$

Subsection 3.1.10 Don't Forget

Don't forget to return to eClass to complete the pre-class quiz.

Subsection 3.1.11 Further Study

Remember that the notes presented above only serve as an introduction to the topic. Further study of the topic will be required. This includes working through the pre-class quizzes, reviewing the lecture notes, and diligently working through the homework problems.

As you study, you should reflect on the following learning outcomes, and critically assess where you are on the path to achieving these learning outcomes:

The following references provide a good start for review and further study:

Learning Outcome Video Textbook Section
1 3.E1, 3.E2 N/A
2 3.E1, 3.E2 N/A
3 3.E3 N/A
4 N/A