Measures of Central Tendency and Spread

Section 10.2 Measures of Central Tendency and Spread

In this section, we continue our study of continuous random variables (such as the height of a randomly chosen MATH 136 student, or the cholesterol level of a randomly chosen female living in Edmonton). We turn our attention to the determination of summary statistics from probability density functions. We focus on two types of statistics, namely measures of central tendency (summarizing typical outcomes of an experiment) and measures of spread (summarizing how similar/varied the outcome of an experiment are).

🔗

Three common measures of central tendency are mean (which the same as average, also known as expected value), median, and mode. Two common measures of spread are variance and standard deviation.

🔗

Subsection 10.2.1 Review: Mean or Average of a Discrete Random Variable

🔗

Recall that the average of a set of discrete values is the sum of the values divided by the number of values in the set. Mathematically, if there are

$n$ values in the set, and the values are denoted

$a_i$ for

$i = 1, 2, \ldots, n\text{,}$ then the average is

$a_{ave} = \frac{a_1 + a_2 + \ldots + a_n}{n} = \frac{1}{n} \sum_{i=1}^n a_i.$

🔗

In preparation for the next section, it is helpful to consider a specific example with repeated values. Suppose that in a group of 10 people:

5 people are 40 years old,
3 people are 12 years old, and
2 people are 7 years old.

🔗

The average age of the 10 people in the group is

$A_{ave} = \frac{ 5(40) + 3(12) + 2(7) }{ 10 } = 25.$ We can rewrite this calculation as follows:

$A_{ave} = 40 \frac{5}{10} + 12 \frac{3}{10} + 7 \frac{2}{10}.$ Note that the fraction 5/10 represents the proportion of people in the group with age 40, that is, the probability that a randomly selected individual from the group is 40 years old. Similarly, the fraction 3/10 represents the probability that a randomly selected individual from the group is 12 years old, etc.

🔗

In the last calculation, the expression on the right-hand side is written in the form of the sum of "outcome times probability of that outcome".

🔗

This form motivates the definition of average of a continuous random variable.

🔗

Subsection 10.2.2 Mean or Average of a Continuous Random Variable

🔗

For the purposes of developing the formula of the mean or average of a continuous random variable, consider the probability density function

$f(x)$ for a continuous random variable

$X$ defined on the interval

$[a,b]\text{.}$

🔗

We will build a Riemann sum:

divide the interval $[a,b]$ into $n$ subintervals of length $\displaystyle \Delta x = \frac{b-a}{n},$ and
let $x_i = a + i \cdot \Delta x$ for $i = 0, 1, 2, \ldots, n\text{,}$

🔗

as shown in the figure below.

🔗
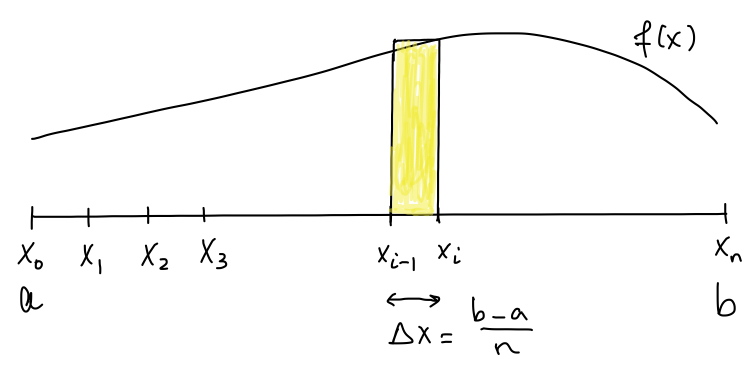
Figure 10.2.1.Illustration of the setup used in the development of the formula of the *mean* or average of a continuous random variable with probability density function $f(x)\text{.}$

🔗

Focus on determining the probability that

$X$ takes on a value between

$x_{i-1}$ and

$x_i\text{.}$ This is the area under the probability density function between

$x_{i-1}$ and

$x_i\text{,}$ which we approximate by the area of the rectangle with width

$\Delta x$ and height

$f(x_i)\text{,}$ that is,

$P( x_{i-1} \le X \le x_{i} ) = \int_{x_{i-1}}^{x_i} f(s) \ ds \approx f(x_i) \Delta x.$ Roughly speaking,

$f(x_i) \Delta x$ is the probability that

$X$ takes on a value approximately equal to

$x_i\text{.}$

🔗

Motivated by the form for the average value from the previous section, namely that the average is the sum of "outcome times probability of that outcome", we thus have

$\begin{alignat*}{1} \text{Average} &= x_0 \cdot f(x_0) \Delta x + x_1 \cdot f(x_1) \Delta x + \ldots + x_n \cdot f(x_n) \Delta x \\ &= \sum_{i=1}^n x_i f(x_i) \Delta x. \end{alignat*}$

🔗

In the limit, as

$n \to \infty\text{,}$ and introducing the notation

$\mu$ for mean or average and

$E[X]$ for expected value, we obtain

$\mu = E[X] = \int_a^b x f(x) \ dx.$

🔗

In general, the mean (average) or expected value of the continuous random variable

$X$ is

$\mu = E[X] = \int_{-\infty}^{\infty} x f(x) \ dx.$

🔗

Subsection 10.2.3 Two Additional Measures of Central Tendency: Median and Mode

🔗

The median, denoted by

$\alpha\text{,}$ is the point at which exactly half the area under the probability density function lies to the left and the other half lies to the right, that is, the median is

$\alpha \text{ such that} \int_{\alpha}^{\infty} f(x) \ dx = \frac{1}{2}.$

🔗

The mode represents the most frequent value(s) of

$X\text{.}$ If the probability density function

$f(x)$ has a single peak, then the mode is the value of

$x$ at which

$f(x)$ has the absolute maximum. In some cases, the probability density function

$f(x)$ has multiple peaks, in which we report multiple modes, each located at a local maximum of

$f(x)\text{.}$

🔗

For symmetric probability density functions with a single peak, the mean, median, and mode are the same. As we have seen, probability density functions often are not symmetric, and it is common for the mean, median, and density to be different. Each measure of central tendency has its advantages and disadvantages. One often determines all three measures of central tendency to obtain insight into the characteristics of a given continuous random variable.

🔗

Remark 10.2.2.

Mean, median, and mode are not the only measures of central tendency. If you are curious about additional measures of central tendency, you may find it interesting to check out this Wikipedia page on Average.

🔗

In the following video, we work through the details of determining the mean, median, and mode for a continuous random variable with a given probability density function.

🔗

Figure 10.2.3. Video demonstrating the determination of the mean, median, and mode for a continuous random variable with a given probability function.

🔗

Subsection 10.2.4 Variance and Standard Deviation of a Continuous Random Variable

🔗

Variance is a measure of how much a random variable is likely to deviate from the mean. The higher the variance, the more spread out the graph of the probability and vice versa.

🔗

The variance of a continuous random variable

$X$ with probability density function

$f(x)$ and mean

$\mu$ is defined as the expected value of the square of the deviation of a random variable from the mean, that is,

$\begin{alignat*}{1} \text{Var}[X] &= E[ ( X - \mu )^2 ] \\ &= \int_{-\infty}^{\infty} (x-\mu)^2 f(x) \ dx = \int_{-\infty}^{\infty} x^2 f(x) \ dx - \mu^2. \end{alignat*}$

🔗

The latter two forms of the variance are equivalent; the last one generally is the easiest to work with in calculations.

🔗

The standard deviation, denoted by

$\sigma$ or SD[

$X$ ], simply is the square root of the variance, that is,

$\sigma = \text{SD}[X] = \sqrt{ \text{Var}[X] }.$

🔗

In the following video, we work through the details of determining the variance and standard deviation for a continuous random variable with a given probability density function.

🔗

Figure 10.2.4. Video demonstrating the determination of the variance and standard deviation for a continuous random variable with a given probability function.

🔗

Subsection 10.2.5 Summary

🔗

Measures of Central Tendency.

A continuous random variable $X$ with probability density function $f(x)$ has the following measures of central tendency:
- The mean, also known as the average or expected value, is $\mu = E[X] = \int_{-\infty}^{\infty} x f(x) \ dx.$
- The median is $\alpha \text{ such that} \int_{\alpha}^{\infty} f(x) \ dx = \frac{1}{2}.$
- The modes are all values of $x$ where $f(x)$ has a local maximum.

🔗

Measures of Spread.

A continuous random variable $X$ with probability density function $f(x)$ has the following measures of spread:
- The variance is
  $\begin{alignat*}{1} \text{Var}[X] &= \int_{-\infty}^{\infty} \left( x - E[X] \right)^2 f(x) \ dx = \int_{-\infty}^{\infty} \left( x - \mu \right)^2 f(x) \ dx \\ &= \int_{-\infty}^{\infty} x^2 f(x) \ dx - (E[X])^2 = \int_{-\infty}^{\infty} x^2 f(x) \ dx - \mu^2. \end{alignat*}$
- The standard deviation is $\sigma = \text{SD}[X] = \sqrt{ \text{Var}[X] }.$

🔗

Subsection 10.2.6 Don't Forget

🔗

Don't forget to return to eClass to complete the pre-class quiz.

🔗

Subsection 10.2.7 Further Study

🔗

Remember that the notes presented above only serve as an introduction to the topic. Further study of the topic will be required. This includes working through the pre-class quizzes, reviewing the lecture notes, and diligently working through the homework problems.

🔗

As you study, you should reflect on the following learning outcomes, and critically assess where you are on the path to achieving these learning outcomes:

🔗

Learning Outcomes

Determine the mean (a.k.a. expected value or average), median, and mode of a continuous random variable given its probability density function (PDF).
Determine the variance and standard deviation of a continuous random variable given its probability density function (PDF).

🔗

The following references provide a good start for review and further study:

Learning Outcome	Video	Textbook Section
1	10.E3	12.5
2	10.E4	12.5