In this section, we begin the study of multi-variable functions. Mathematically, we are interested in a function of two variables, for example z=f(x,y)=sin(x+y), or in a function of three variables, for example f(x,y,z)=x2+y2+z2, or more generally in a function of n variables, f(x1,x2,…,xn).
Formally, a function of two variables, f, is a rule that assigns to each point (x,y) in the domain D a real number z=f(x,y). Functions of two variables define surfaces in R3 which we often can visualize.
If f is a function of two independent variables with domain D, then the graph of f is the set of all points (x,y,z) such that z=f(x,y) for all (x,y) in D.
Note that we now work with coordinate triplets, (x,y,z). We locate each point (x,y,z) in R3 using the Cartesian coordinate system. An example of a surface visualized in R3 is the blue shape in the left figure below:
Figure11.2.1.On the left, a surface and its level curves. On the right, a contour plot. Source: Biocalculus: Calculus for the Life Sciences, James Stewart and Troy Day, Cengage Learning, 2015.
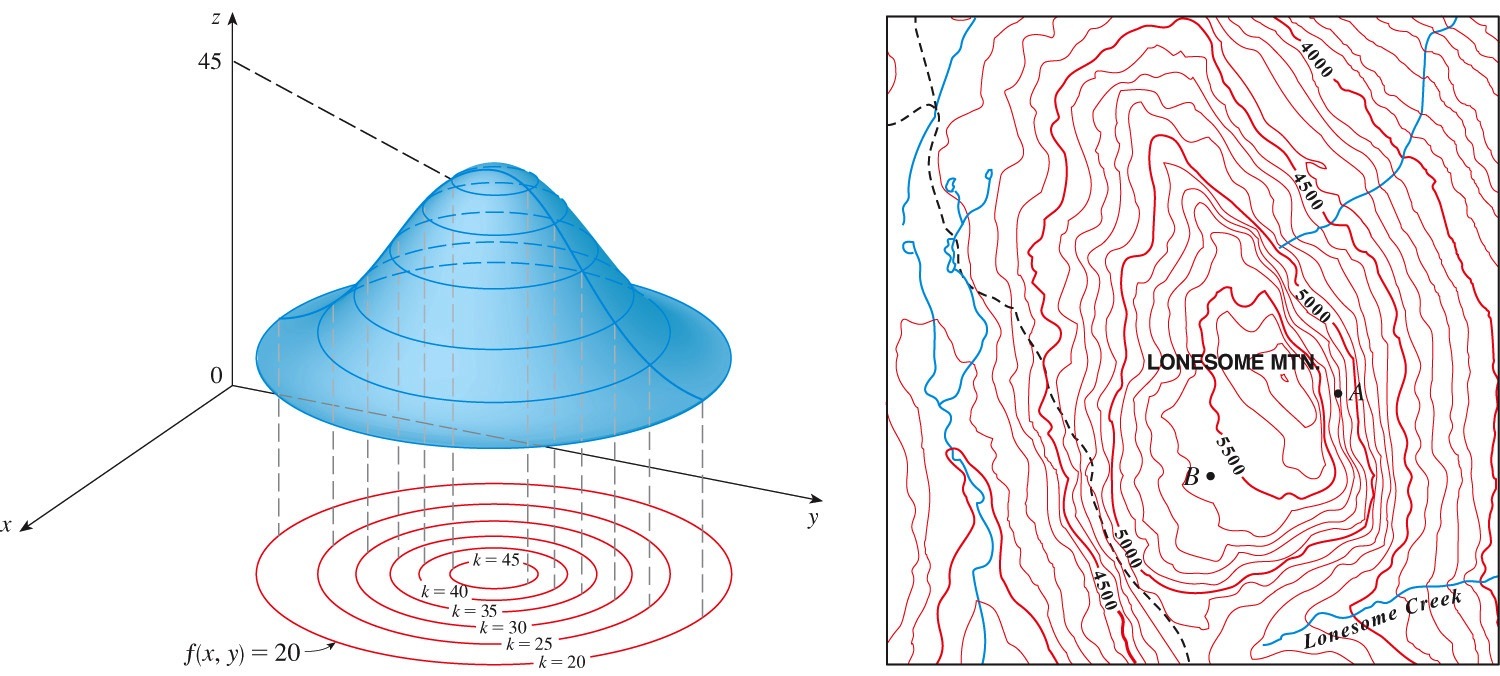
A complementary method to visualize functions of two variables is the contour plot. A contour plot is like a topographical map showing the level curves (see the right figure above).
In what follows, we present two specific examples. For each example, we show the surface in R3 on the left, and level curves in the corresponding contour plot immediately to the right.
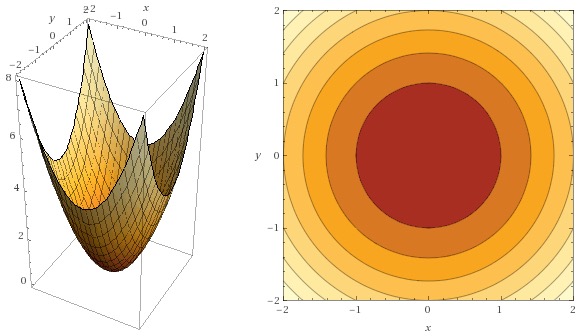
Figure11.2.2.Visualization of the surface z=f(x,y)=x2+y2 (left) and its level curves (right). Credit: Generated by WolframAlpha using the command plot x^2 + y^2, x=-2..2 y=-2..2.
To connect the equation of the surface, z=f(x,y)=x2+y2, to its visualizations, recall that x2+y2=R2 is the equation of a circle with radius R centered at the origin in the xy plane. Therefore, each level curve given by x2+y2=k is a circle with radius √k centered at the origin in the xy plane. Equivalently, the intersection of the horizontal plane z=k (any plane that is parallel to the xy plane) and the surface is a circle with radius √k. The larger the value of k, the larger the circle.
The circles are clearly shown in the contour plot. Here, seven level curves x2+y2=k are shown, for k=1,2,…,7. The level curve given by k=4 is a circle of radius 2 in the xy plane.
Take a moment to locate the level curve for \(k=4\) in the contour plot, and verify that it is a circle passing through the points \((\pm 2,0)\) and \((0, \pm 2)\text{.}\)
The surface is called a paraboloid. Note that the intersection of the surface with the yz plane (defined by x=0) is the parabola z=y2. Similarly, the intersection of the surface with the xz plane (defined by y=0) is the parabola z=x2.
Take a moment to imagine the location of the \(yz\) and \(xz\) planes in the plot in \(\mathbb{R}^3\) above, and verify that their intersections with the surface appear to be parabolas.
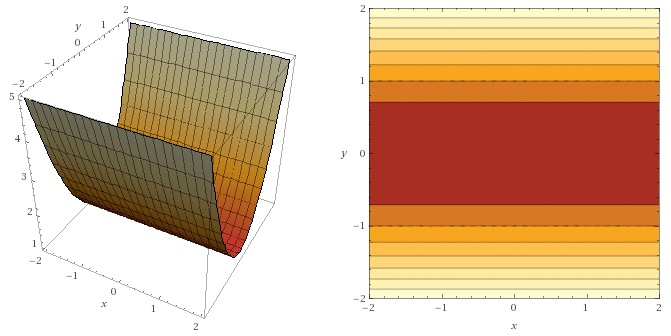
Figure11.2.5.Visualization of the surface z=f(x,y)=1+y2 (left) and its level curves (right). Credit: Generated by WolframAlpha using the command plot3d 1 + y^2, x=-2..2 y=-2..2.
To connect the equation of the surface, z=f(x,y)=1+y2, to its visualizations, note that is independent of the value of x. That is, the intersection of each vertical plane x=c (any plane parallel to the yz plane) with the surface is the parabola z=1+y2.
The level curves are 1+y2=k, that is y=√k−1, which are horizontal lines (as expected, since the surface is independent of x), as seen in the contour plot.
To view the surface $$ z= f(x,y) = \sin \left( \sqrt{x^2 + y^2} \right) $$ and the corresponding contour plot with WolframAlpha, use the command plot sin( sqrt( x^2 + y^2 ) ).
To view the surface $$ z= f(x,y) = (x^2 - y^2)^2 $$ and the corresponding contour plot with WolframAlpha, use the command plot ( x^2 - y^2 )^2, x=-3..3 y=-3..3.
To view the surface $$ z= f(x,y) = \sin \left( |x| + |y| \right) $$ and the corresponding contour plot with WolframAlpha, use the command plot sin( abs(x) + abs(y) ), x=-6..6 y=-6..6.
Unfortunately, we are not able to visualize functions of three or more variables very easily, as we would need to visualize in R4 or higher-dimensional space. To gain insight into how these functions behave, one might think about the behaviour on certain convenient cross-sections by setting one or more variables equal to a constant (similar to what we did in the previous section, for example by considering the intersection of the horizontal plane z=k with the surface). This is not easy though, and certainly not a learning outcome for this course.
If f is a function of two independent variables with domain D, then the graph of f is the set of all points (x,y,z) such that z=f(x,y) for all (x,y) in D.
A level curve of z=f(x,y) consists of the points (x,y) in the xy plane with equations f(x,y)=k, where k is a constant in the range of f.
A contour plot is a graph in the xy plane with a set of level curves of z=f(x,y).
Remember that the notes presented above only serve as an introduction to the topic. Further study of the topic will be required. This includes working through the pre-class quizzes, reviewing the lecture notes, and diligently working through the homework problems.
As you study, you should reflect on the following learning outcomes, and critically assess where you are on the path to achieving these learning outcomes:
