Traversals

A traversal is a way of moving through a structure. With trees, there are several ways of moving through them including depth-first and breadth-first.

In depth-first traversal, we move quickly to the bottom of the tree (diving deep) before moving to the right at the same level; in breadth-first traversal, we stay at the same level until we’ve visited everything there before moving any deeper. Depth-first traversals include pre-order traversal, post-order traversal, and Euler traversal. For binary trees, we will also investigate an additional depth-first traversal called in-order traversal.

Pre-order Traversal

In pre-order traversal, we dive deep, visiting as we dive, and we move left before we move right. A node is visited before its proper descendants, and a node on the left is visited before a node on the right. The root is always the first node visited. The algorithm is as follows, with the root as the starting node when first called:

Algorithm preOrderTraversal(\(aNode\))

1. visit(\(aNode\))
   

2. for each child \(c\) of \(aNode\), in order from left to right
   \(\;\;\;\;\;\) preOrderTraversal(\(c\))
   

A pre-order traversal on our example tree:

Example Tree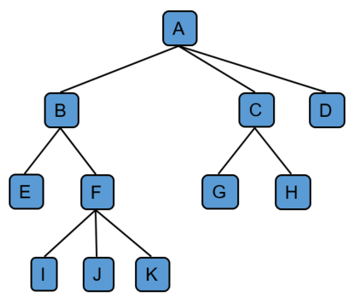

Pre-order Traversal A, B, E, F, I, J, K, C, G, H, D

Pre-order Traversal on a Binary Tree

For a binary tree, the algorithm may be simplified to account for the maximum of two children at each node.

For Binary Trees Only

Algorithm preOrderTraversal(\(aNode\))

1. visit(\(aNode\))
   

2. if \(aNode\).hasLeftChild()
   \(\;\;\;\;\;\) preOrderTraversal(\(aNode\).getLeftChild())
   

3. if \(aNode\).hasRightChild()
   \(\;\;\;\;\;\) preOrderTraversal(\(aNode\).getRightChild())
   

A pre-order traversal on this binary tree:

Example Tree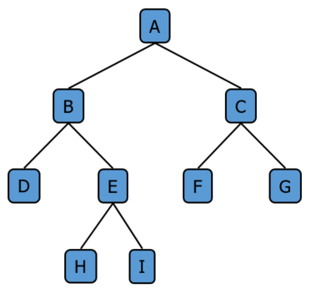

Pre-order Traversal A, B, D, E, H, I, C, F, G

Post-order Traversal

Post-order traversal is much the same as the previous traversal, still diving deep, with the only difference being where we do the visit of the node. We skip through nodes until we reach the bottom-most left-most node. A node is visited after all of its proper descendants have been visited. The algorithm is as follows, with the root as the starting node but the last node actually visited.

Algorithm postOrderTraversal(\(aNode\))

1. for each child \(c\) of \(aNode\), in order from left to right
   \(\;\;\;\;\;\) postOrderTraversal(\(c\))
   

2. visit(\(aNode\))
   

A post-order traversal on our example tree:

Example Tree

Post-order Traversal E, I, J, K, F, B, G, H, C, D, A

Post-order Traversal on a Binary Tree

For a binary tree, the algorithm may be simplified to account for the maximum of two children at each node.

For Binary Trees Only

Algorithm postOrderTraversal(\(aNode\))

1. if \(aNode\).hasLeftChild()
   \(\;\;\;\;\;\) postOrderTraversal(\(aNode\).getLeftChild())
   

2. if \(aNode\).hasRightChild()
   \(\;\;\;\;\;\) postOrderTraversal(\(aNode\).getRightChild())
   

3. visit(\(aNode\))
   

A post-order traversal on this binary tree:

Example Tree

Post-order Traversal D, H, I, E, B, F, G, C, A

In-order Traversal

This last traversal only applies to binary trees. In-order traversal is still a depth-first traversal starting at the root. The visit of a node occurs between the visit to each of its children. In other words, we visit the left child, the parent, and then the right child. The algorithm is:

For Binary Trees Only

Algorithm inOrderTraversal(\(aNode\))

1. if \(aNode\).hasLeftChild()
   \(\;\;\;\;\;\) inOrderTraversal(\(aNode\).getLeftChild())
   

2. visit(\(aNode\))
   

3. if \(aNode\).hasRightChild()
   \(\;\;\;\;\;\) inOrderTraversal(\(aNode\).getRightChild())
   

An in-order traversal on this binary tree:

Example Tree

In-order Traversal D, B, H, E, I, A, F, C, G

Euler Traversal

If we wanted to, we could do work, that is visit(), a node every time we come through it - on our first encounter with the node, on our way down to each child, and on our way up from each child. This is the Euler Traversal.

Algorithm eulerTraversal(\(aNode\))

1. visit(\(aNode\))
   

2. for each child \(c\) of \(aNode\), in order from left to right
   \(\;\;\;\;\;\) a. eulerTraversal(\(c\))
   \(\;\;\;\;\;\) b. visit(\(aNode\))
   

An Euler traversal on our example tree:

Example Tree

Euler Traversal A, B, E, B, F, I, F, J, F, K, F, B, A, C, G, C, H, C, A, D, A

This shows how the traversal process moves through the tree:

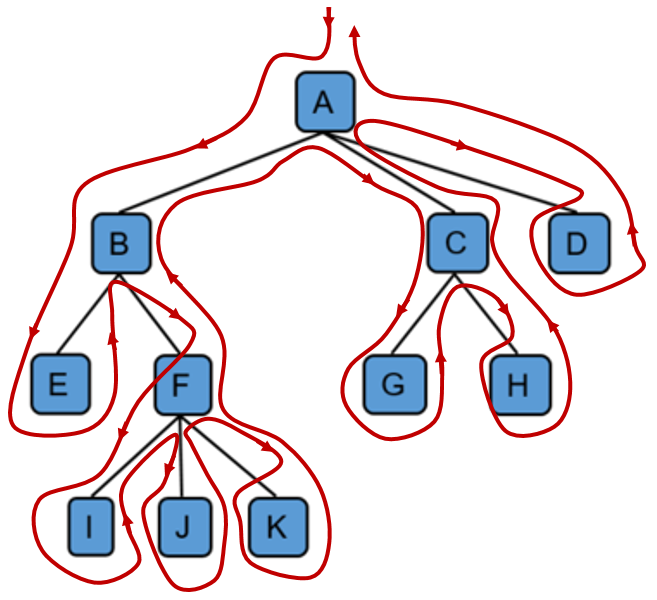
Breadth-first Traversal

In breadth-first traversal, the tree is visited level-by-level and left to right. In order to implement this, we need to use the queue data structure in addition to the tree so that we maintain our ordering. For this reason, such a traversal is not popular. Here is an algorithm:

Algorithm breadthFirstTraversal(\(aQueue\))
\(\;\;\;\;\;\) Note: start \(aQueue\) containing only the root of the tree

1. As long a \(aQueue\) is not empty
   \(\;\;\;\;\;\) a. \(aNode ← aQueue.dequeue()\)
   \(\;\;\;\;\;\) b. visit(\(aNode\))
   \(\;\;\;\;\;\) c. for each child \(c\) of \(aNode\), in order from left to right
   \(\;\;\;\;\;\;\;\;\;\;\) aQueue.enqueue(\(c\))
   \(\;\;\;\;\;\) d. breadthFirstTraversal(\(aQueue\))

A breadth-first traversal on this binary tree:

Example Tree

Breadth-first Traversal A, B, C, D, E, F, G, H, I J, K

Practice Questions

1. Given the following tree:
   

   

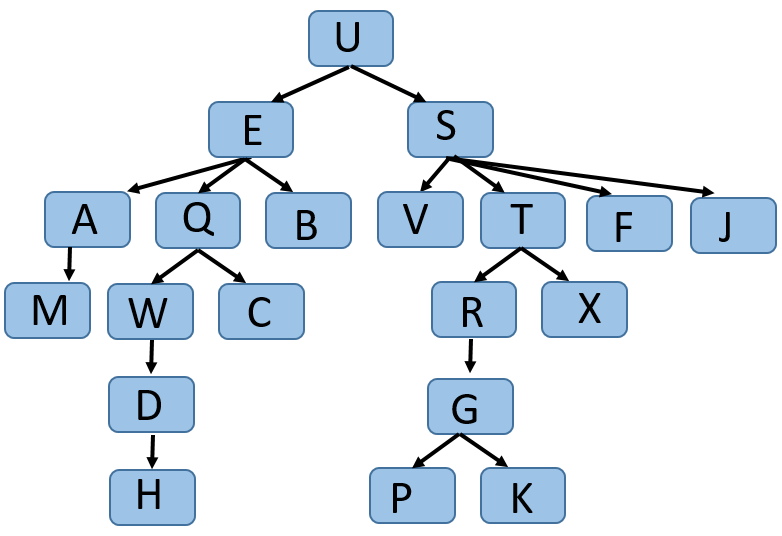
   a. What is the post-order traversal?
   b. What is the pre-order traversal?
   c. What is the in-order traversal?
   d. What is the Euler traversal?
   e. What is the breadth-first traversal?
   f. What would the queue contain when T is visited under breadth-first search?

2. Construct a tree so that its pre-order traversal is COMESANTA and its post-order traversal is OSNATAEMC.

3. Construct a tree so that its pre-order traversal is ALMOSTDONE and its post-order traversal is LOMNOEDTSA.

4. When is the queue of a breadth-first traversal empty?

5. Given the following tree:
   

   

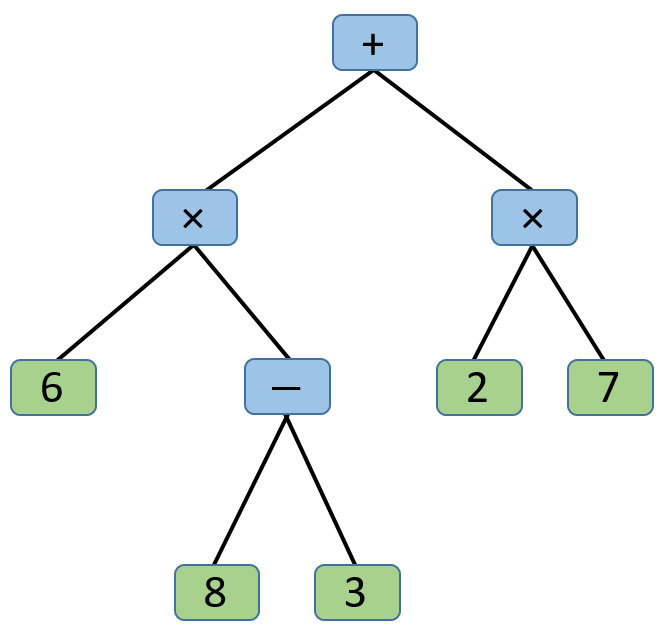
   a. Evaluate the arithmetic expression given by this tree. Write the expression using regular (infix) mathematical notation. Notice how the tree makes the expression unambiguous, but to write it down requires parentheses.
   
   b. Write the post-order traversal. This yields postfix form for an arithmetic expression, which is unambiguous without parentheses required.
   
   c. Write the pre-order traversal. This yields prefix form for an arithmetic expression, which is again unambiguous without parentheses required.
   
   

To Solutions