Solutions to the Practice Questions

Example - Printing Characters Using Both Loop and Recursion

1. The base case is aNum <= 0. In the base case, the method ends and returns without doing anything.

2. The recursive call is printNumChars(aNum - 1, aChar). Since it is subtracting 1 from aNum, this ensures that eventually aNum will be 0, putting the execution into base case.

Back to Questions

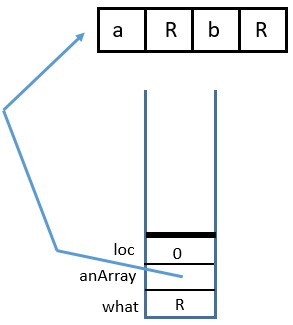
Example - Sum an Array with Both Loop and Recursion

1. The base case is loc >= anArray.length.

2. The recursive call is sumArrayTRSub(anArray, loc + 1, sum + anArray[loc]) so loc has 1 added to it each time. This guarantees that eventually loc will exceed the array’s length, putting the execution into the base case.

3. Here is the trace:

   1 Call Call sumArrayTRSub(myArray, 0, 0)	2 Call sumArrayTRSub(myArray, 1, 5)
   3 Call sumArrayTRSub(myArray, 2, 2)	4 Call sumArrayTRSub(myArray, 3, 10)
   5 Return from sumArrayTRSub(myArray, 3, 10)	6 Return from sumArrayTRSub(myArray, 2, 2)
   7 Return from sumArrayTRSub(myArray, 1, 5)	8 Return from sumArrayTRSub(myArray, 0, 0)

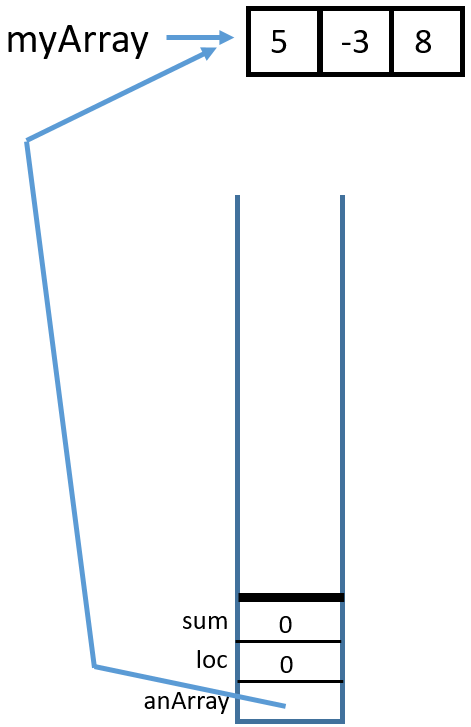
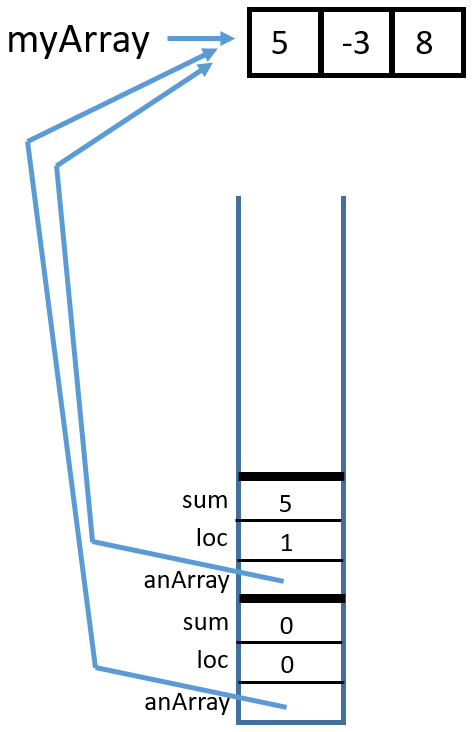
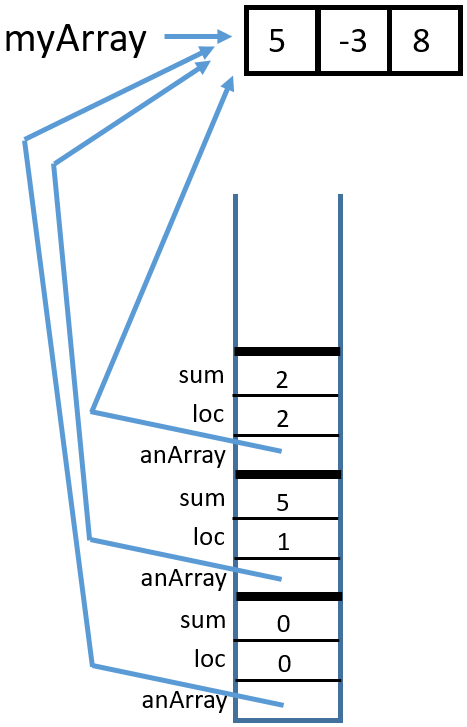
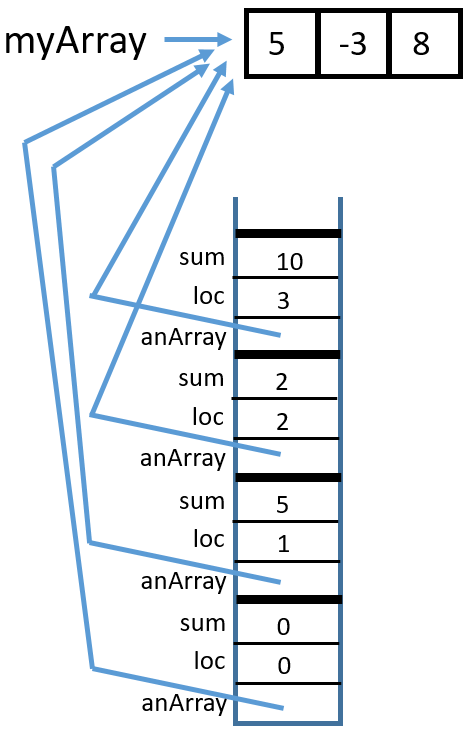
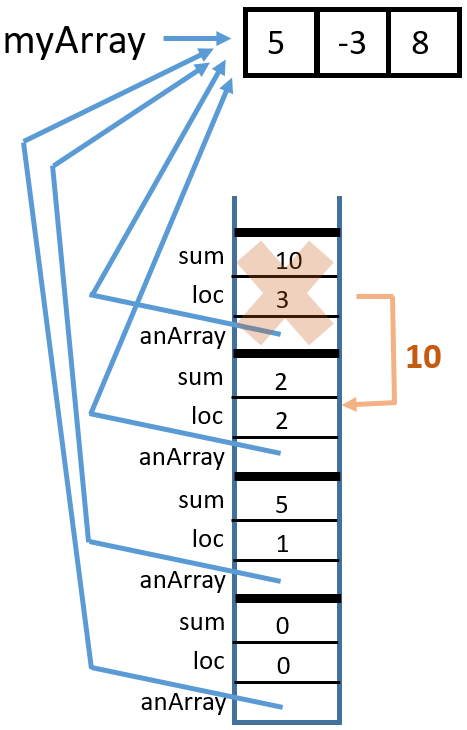
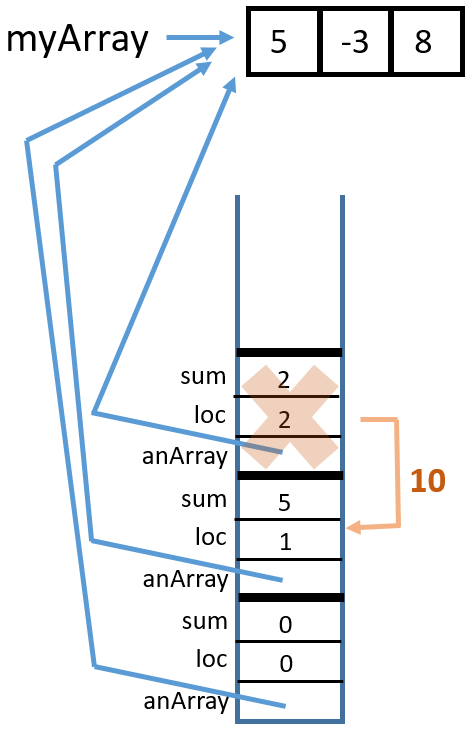
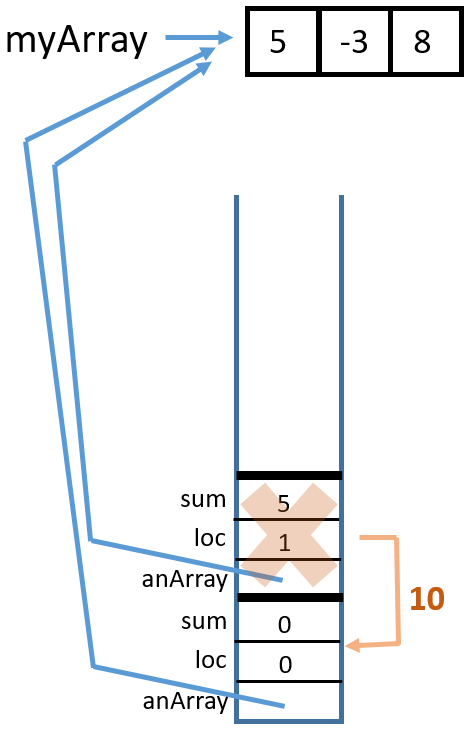
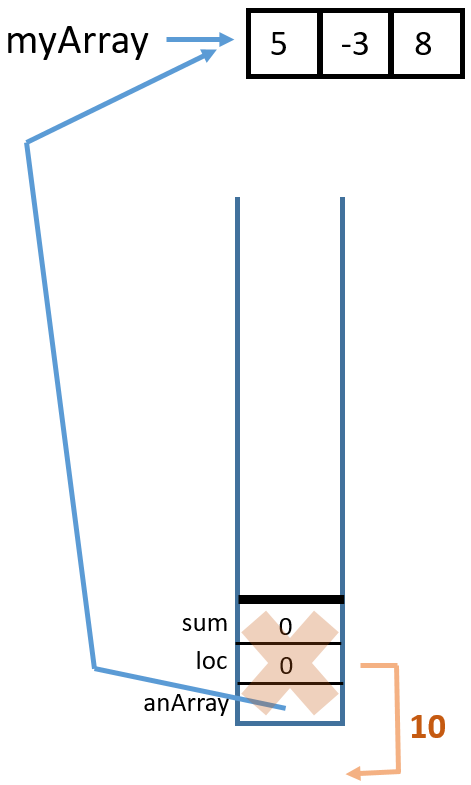
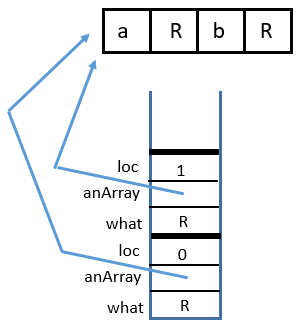
4. Here is the trace:

   1 Call Call sumArrayTRSub(myArray, 2, 0)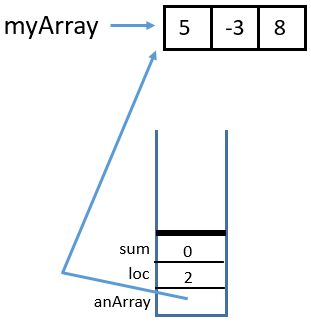	2 Call sumArrayTRSub(myArray, 3, 8)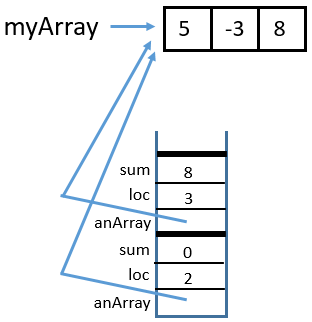
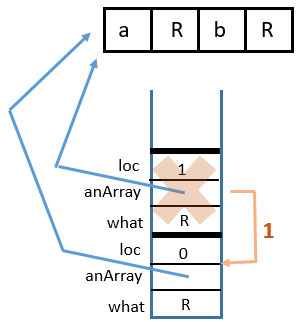
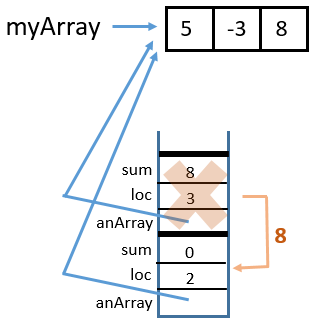
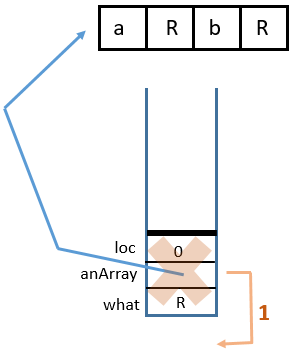
   3 Return from sumArrayTRSub(myArray, 3, 8)	4 Return from sumArrayTRSub(myArray, 2, 0)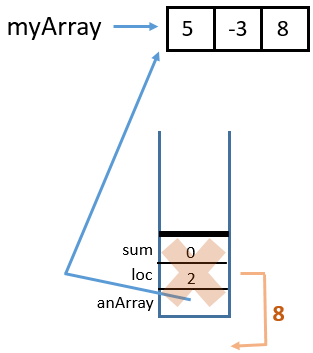

Back to Questions

Example - Power Function With Recursion

1. There is one base case, when y is 0.

2. There are two recursive calls, one in the else if, namely power(x, -y), and one in the else, namely power(x, y - 1).

3. y needs to become 0, so if it was negative then making it positive ensures that subtracting one will eventually make y equal to 0. If y was positive to start with, then subtracting one will eventually make y zero.

4. Here is the trace:

   1 Call power(25, 3)	2 Call power(25, 2)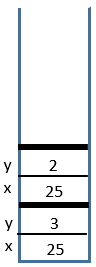
   3 Call power(25, 1)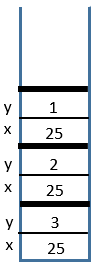	4 Call power(25, 0)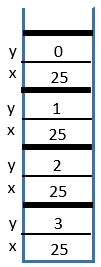
   5 Return from power(25, 0)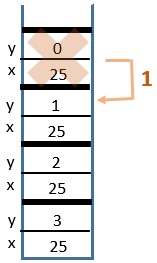	6 Return from power(25, 1)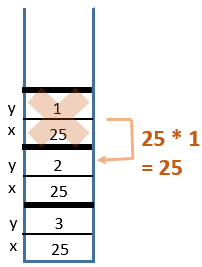
   7 Return from power(25, 2)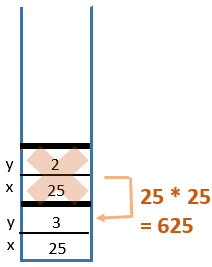	8 Return from power(25, 3)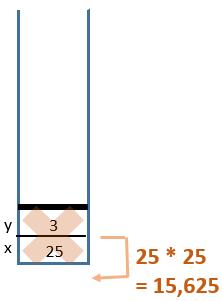

5. Here is the trace:

   1 Call power(3, -1)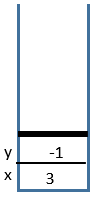	2 Call power(3, 1)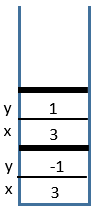
   3 Call power(3, 0)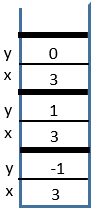	4 Return from power(3, 0)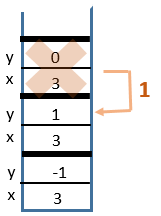
   5 Return from power(3, 1)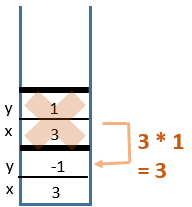	6 Return from power(3, -1)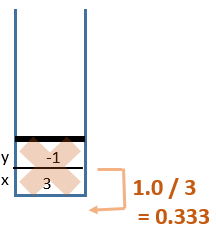

6. No. The result is built after the recursive call. As the stack is being popped, the return value then multiplies with x. The recursive call is not the last thing before base case.

7. public static double power(int x, int y){
      if (y == 0){ //Added this to make recursion faster, can end at 1 now
         return 1;
      }
      if (y < 0){
         return 1.0 / powerSub(x, -y);
      }
      return powerSub(x, y);
   }
   
   private static double powerSub(int x, int y){
      if (y == 1){ //Saving a stack frame over y == 0
         return x;
      }
      else {
         return x * powerSub(x, y - 1);
      }
   } 
   

Back to Questions

Sequential Search Recursively

1. There are two base cases: loc >= anArray.length or what == anArray[loc]. This is when the array has been exhausted or the item has been found.

2. There is one recursive call, in the last line of code in the method: seqSearch(what, anArray, loc + 1)

3. loc changes so that it moves through the indices of the array. Since one is being added to loc we guarantee to reach the length of the array.

4. seqSearch(char, char[])

5. Here is a stack trace:

   1 Call seqSearch('R', {'a', 'R', 'b', 'R'}, 0)	2 Call seqSearch('R', {'a', 'R', 'b', 'R'}, 1)
   3 Return from seqSearch('R', {'a', 'R', 'b', 'R'}, 1)	4 Return from seqSearch('R', {'a', 'R', 'b', 'R'}, 0)

6. Yes. The recursive call is the last thing done before base case is reached, so the value returned is simply passed down the stack.

Back to Questions

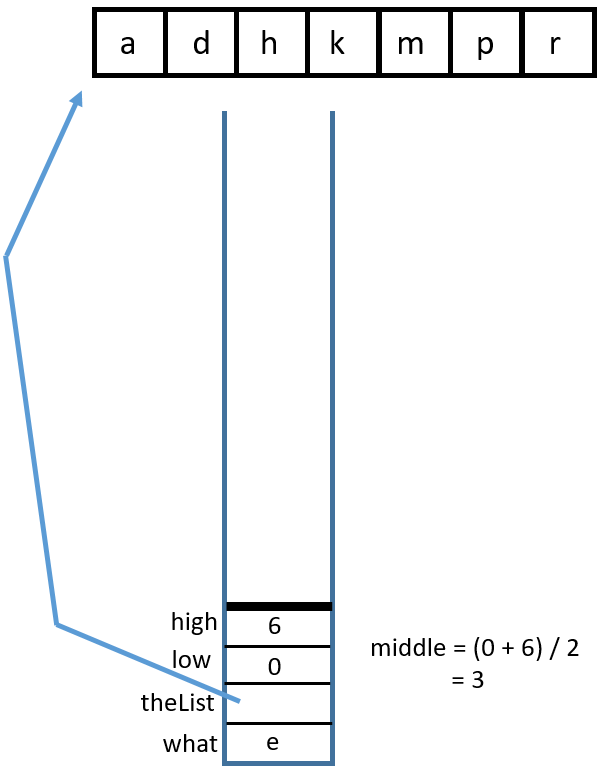
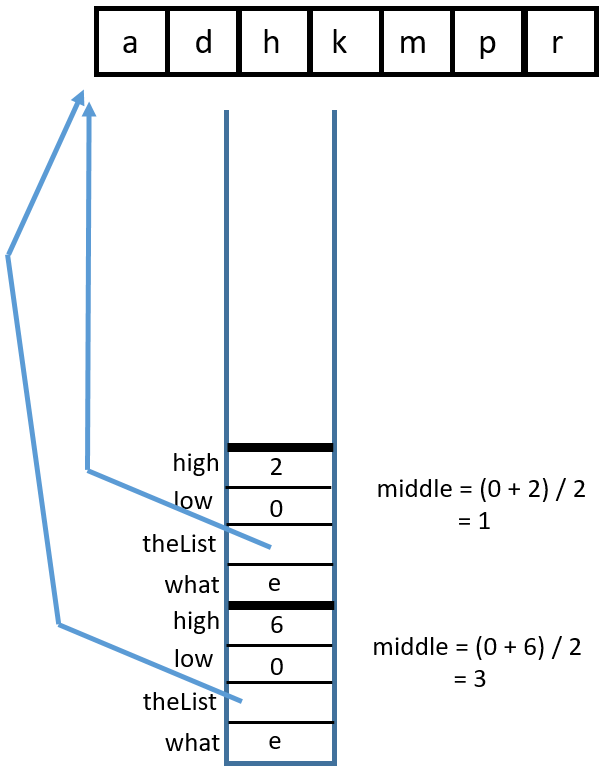
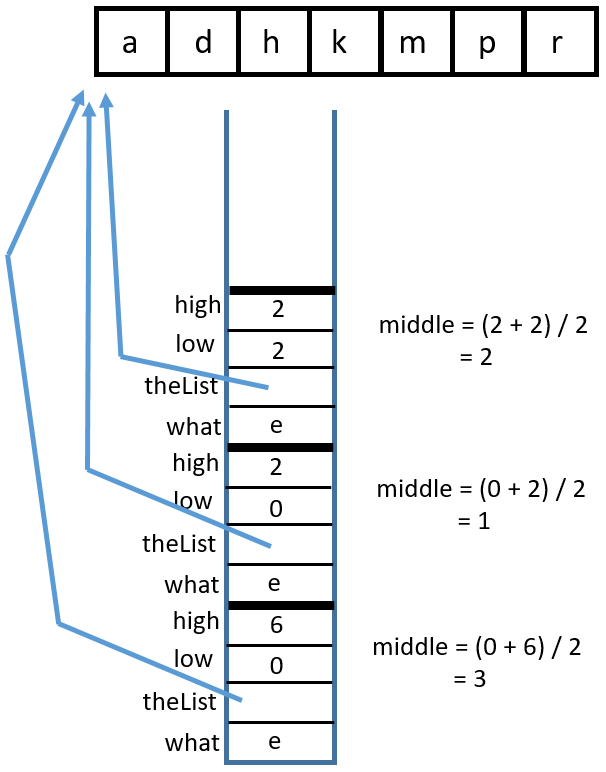
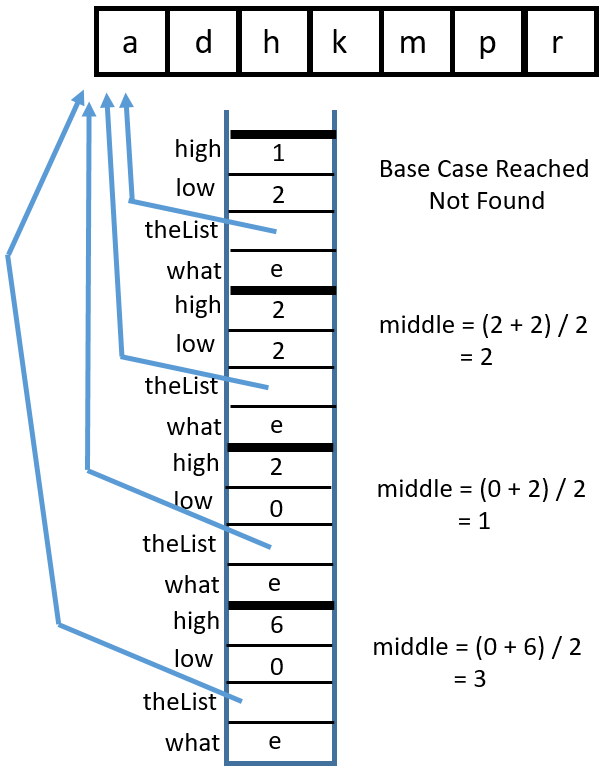
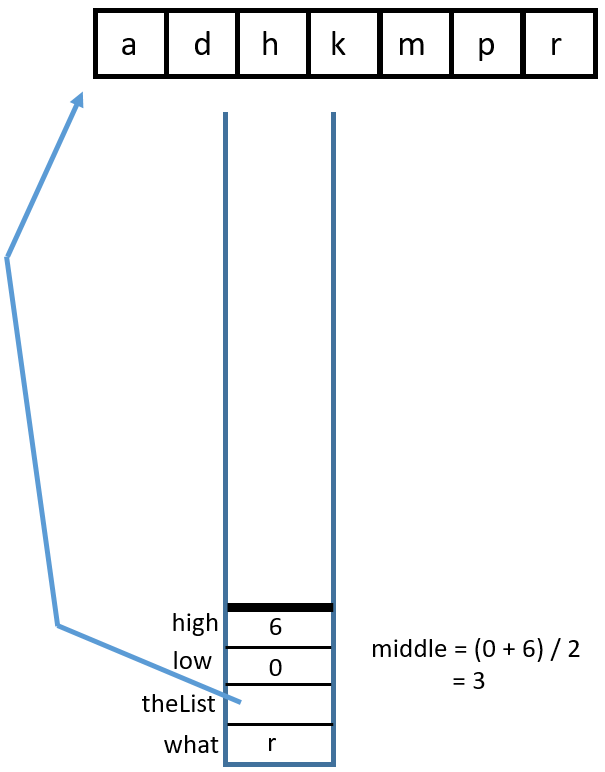
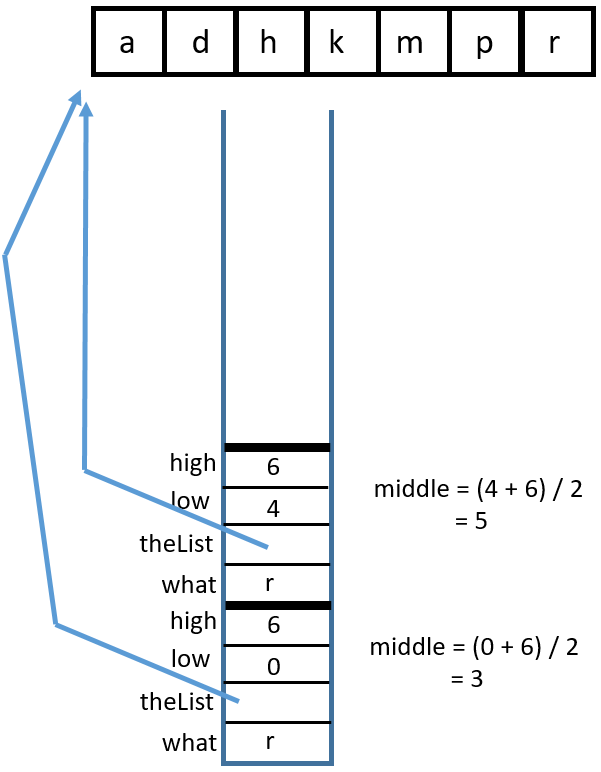
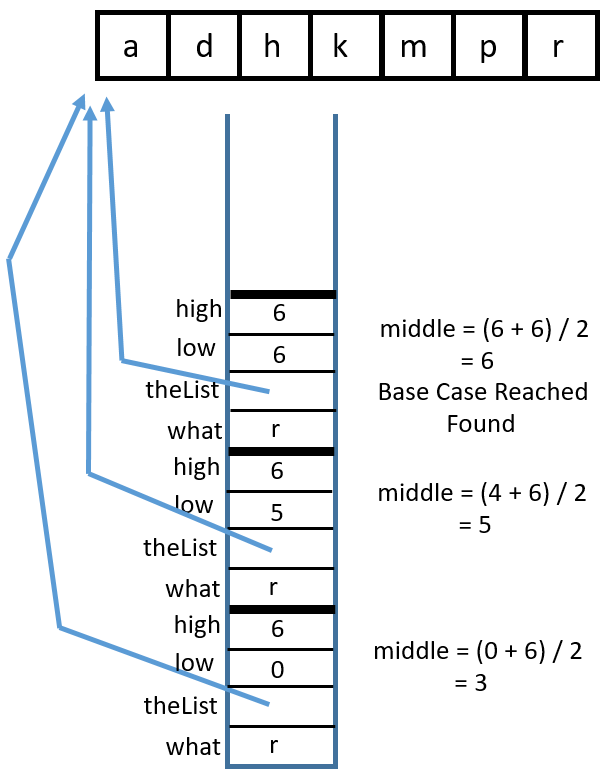
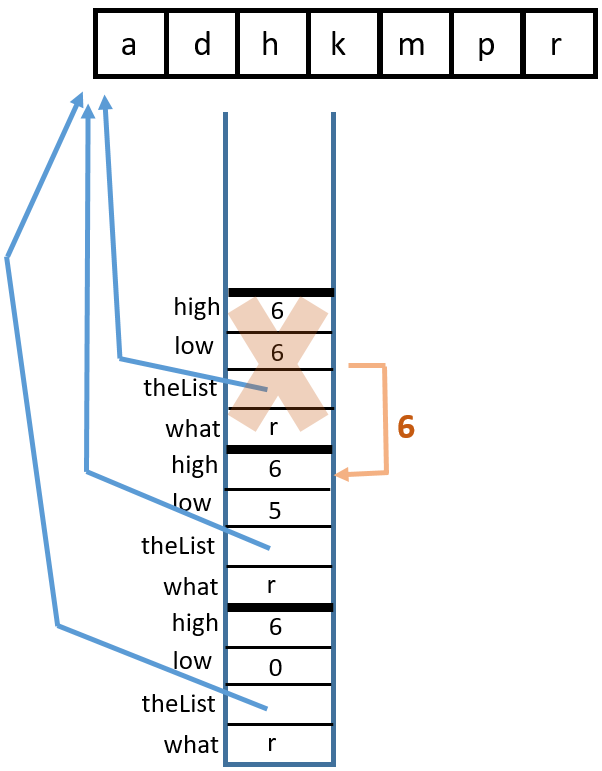
Binary Search Recursively

1. There are two base cases: high < low or theList[middle] == what. These are for identifying if enough places have been checked or if the item has been found.

2. There are two recursive calls: binarySearch(what, theList, middle + 1, high) and binarySearch(what, theList, low, middle - 1)

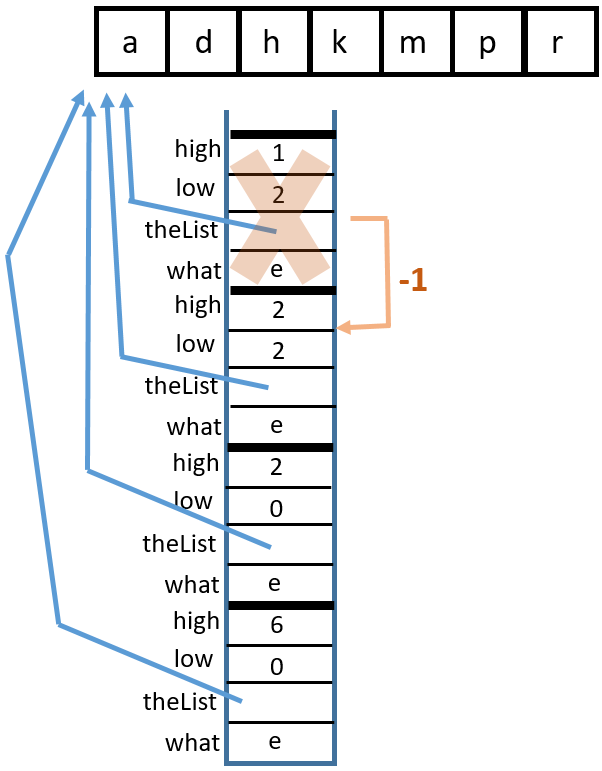
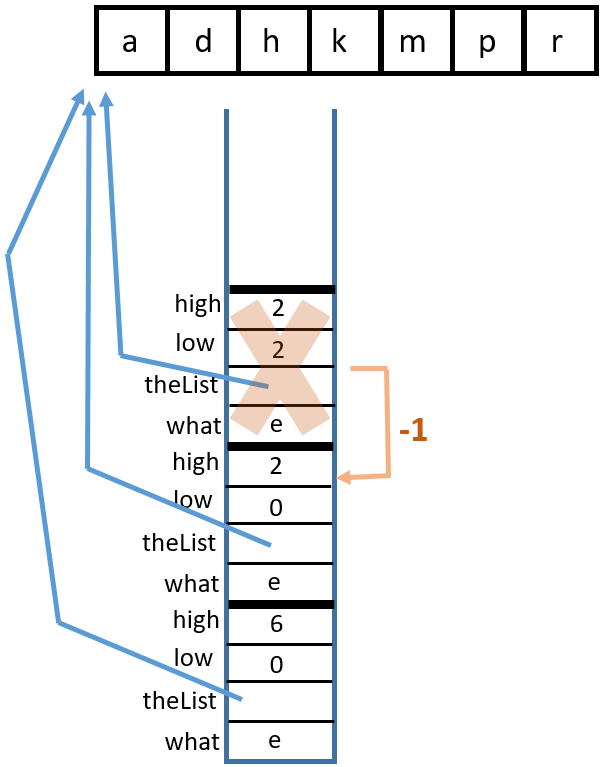
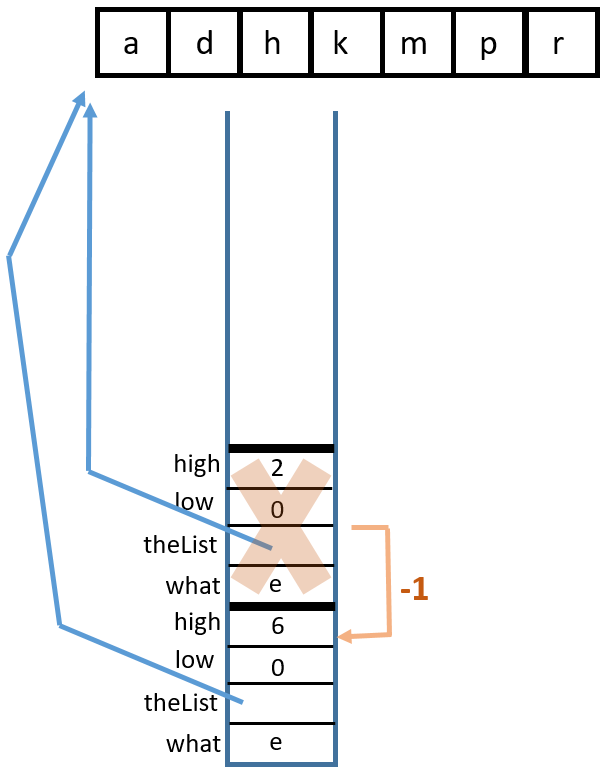
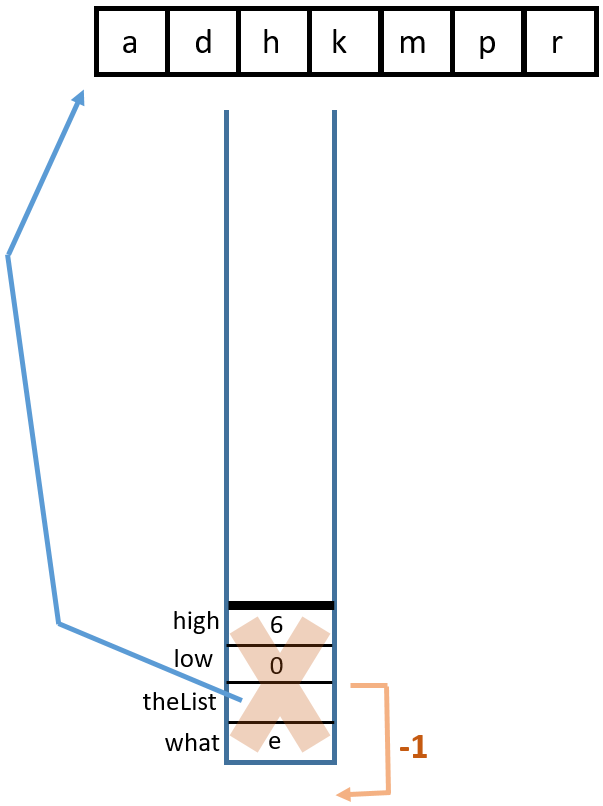
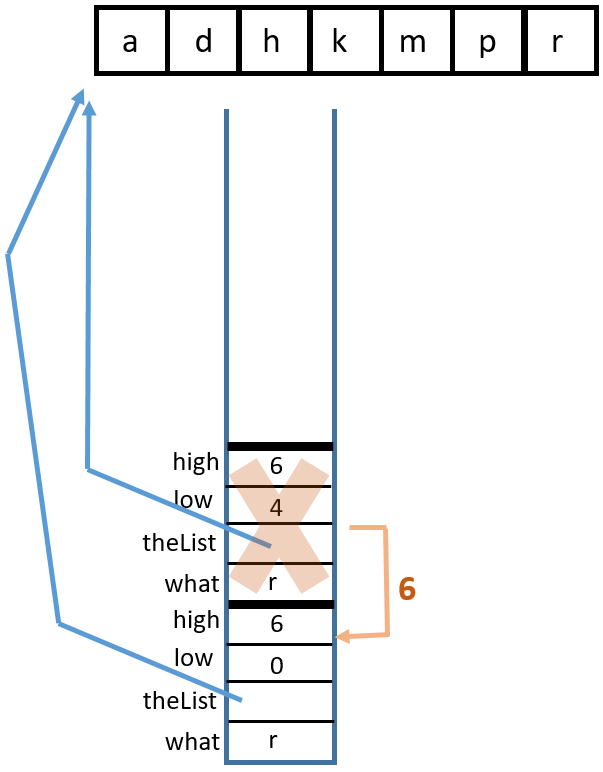
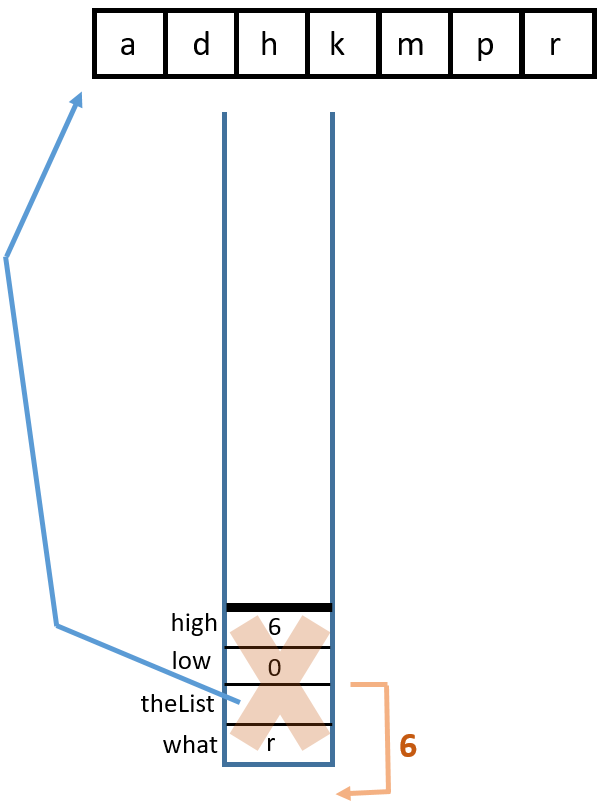
3. Either low is incremented or high is decremented, eventually leading to high becoming less than low.

4. binarySearch(char, char[])

5. You can visualize this with a binary search tree or with a stack diagram. Binary search tree:

   

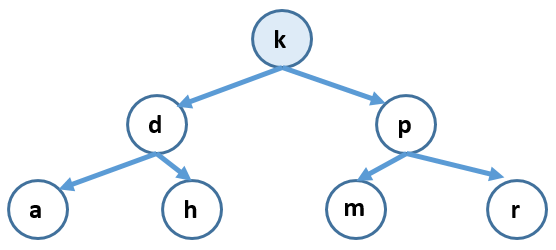
   Stack diagram:

   1 Call binarySearch('k', {'a', 'd', 'h', 'k', 'm', 'p', 'r'}, 0, 6)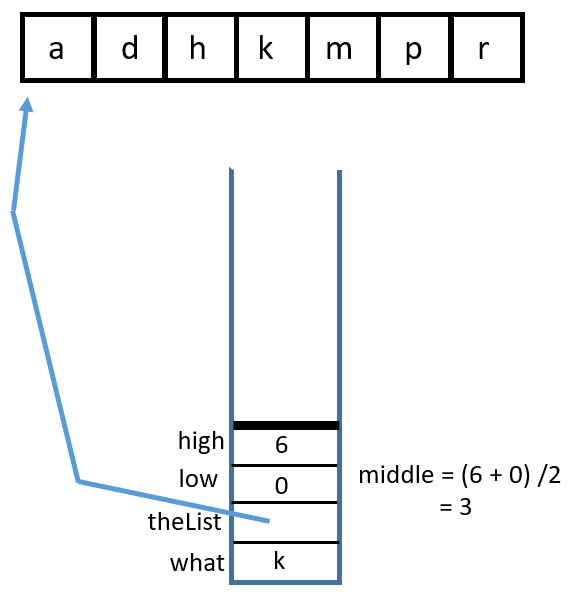

   2 Return from binarySearch('k', {'a', 'd', 'h', 'k', 'm', 'p', 'r'}, 0, 6)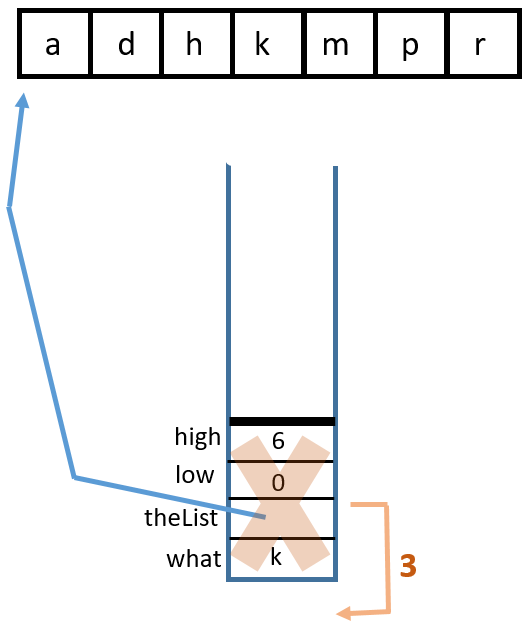

6. You can visualize this with a binary search tree or with a stack diagram. Binary search tree:

   

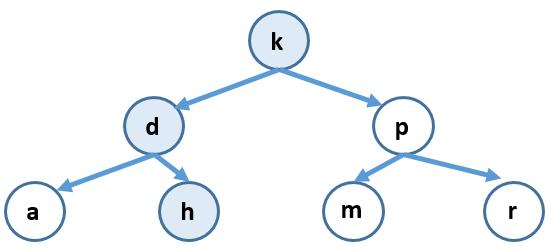
   Stack diagram:

   1 Call binarySearch('e', {'a', 'd', 'h', 'k', 'm', 'p', 'r'}, 0, 6)	2 Call binarySearch('e', {'a', 'd', 'h', 'k', 'm', 'p', 'r'}, 0, 2)
   3 Call binarySearch('e', {'a', 'd', 'h', 'k', 'm', 'p', 'r'}, 2, 2)	4 Call binarySearch('e', {'a', 'd', 'h', 'k', 'm', 'p', 'r'}, 2, 1)
   5 Return from binarySearch('e', {'a', 'd', 'h', 'k', 'm', 'p', 'r'}, 2, 1)	6 Return from binarySearch('e', {'a', 'd', 'h', 'k', 'm', 'p', 'r'}, 2, 2)
   7 Return from binarySearch('e', {'a', 'd', 'h', 'k', 'm', 'p', 'r'}, 0, 2)	8 Return from binarySearch('e', {'a', 'd', 'h', 'k', 'm', 'p', 'r'}, 0, 6)

7. You can visualize this with a binary search tree or with a stack diagram. Binary search tree:

   

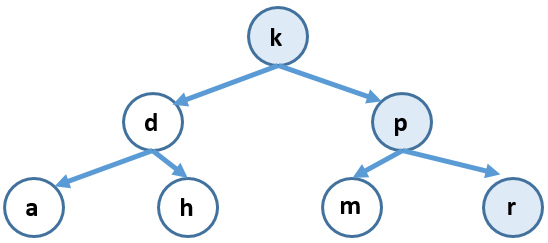
   Stack diagram:

   1 Call binarySearch('r', {'a', 'd', 'h', 'k', 'm', 'p', 'r'}, 0, 6)	2 Call binarySearch('r', {'a', 'd', 'h', 'k', 'm', 'p', 'r'}, 0, 2)
   3 Call binarySearch('r', {'a', 'd', 'h', 'k', 'm', 'p', 'r'}, 2, 2)	4 Return from binarySearch('r', {'a', 'd', 'h', 'k', 'm', 'p', 'r'}, 2, 2)
   5 Return from binarySearch('r', {'a', 'd', 'h', 'k', 'm', 'p', 'r'}, 0, 2)	6 Return from binarySearch('r', {'a', 'd', 'h', 'k', 'm', 'p', 'r'}, 0, 6)

8. Size 7: 3
   Size 15: 4
   Size \(n\): \(\log_2 (n + 1)\)

9. Yes. The recursive call is the last thing done before base case is reached, so the value returned is simply passed down the stack.

Back to Questions

Quicksort

1.    Original: { 24,  67, 102,  14,  90,  55,  10,  76,  92,  59}  pivot: 59
    First Pass: { 24,  10,  55,  14,  59, 102,  67,  76,  92,  90}  pivot: 14 and 90
   Second Pass: { 10,  14,  55,  24,  59,  76,  67,  90,  92, 102}  pivot: 24, 67, 102
    Third Pass: { 10,  14,  24,  55,  59,  67,  76,  90,  92, 102}  now all base cases
   

2.    Original: {7, 6, 5, 4, 3, 2, 1}  pivot: 1
    First Pass: {1, 6, 5, 4, 3, 2, 7}  pivot: 7
   Second Pass: {1, 6, 5, 4, 3, 2, 7}  pivot: 2
    Third Pass: {1, 2, 5, 4, 3, 6, 7}  pivot: 6
   Fourth Pass: {1, 2, 5, 4, 3, 6, 7}  pivot: 3
    Fifth Pass: {1, 2, 3, 4, 5, 6, 7}  pivot: 5
    Sixth Pass: {1, 2, 3, 4, 5, 6, 7}  now base case
   

3.    Original: {97, 68, 75, 34, 45, 60}  pivot: 60
    First Pass: {45, 34, 60, 68, 97, 75}  pivot: 34, 75
   Second Pass: {34, 45, 60, 68, 75, 97}  now all base cases
   

4. /**
    * Returns the location of the median of the first, middle, and last
    * items in the list.  
    * 
    * @param aList - list of size 3 or more, all unique
    * @return - index (0-based) of the median of first, middle and last
    */
   public static int getMedianLoc(int[] aList){     
       int middleLoc = aList.length / 2;
       int lastLoc = aList.length - 1;
   
       int first = aList[0];
       int middle = aList[middleLoc];
       int last = aList[lastLoc];
   
       if (first < middle){
           if (middle < last){ //first < middle < last
               return middleLoc;
           }
           else if (first < last){ //first < last < middle
               return lastLoc;
           }
           else{ //last < first < middle
               return 0; 
           }
       }
       else{ //middle < first
           if (first < last){ //middle < first < last
               return 0; //first location
           }
           else if (middle < last){ //middle < last < first
               return lastLoc;
           }
           else{ //last < middle < first
               return middleLoc;
           }
       }
   }
   

5. /**
     * Finds a pivot in aList as the median of three and moves the pivot
     * to the end of the list, putting the original ending element in
     * where the median was.  
     * 
     * @param aList - list of size 3 or more, all unique
     */
    public static void pivotToEnd(int[] aList){
        swap(aList, getMedianLoc(aList), aList.length - 1);
    }
   

6. Change the inequality sign in two places in the partition algorithm.
   while ((left <= right && aList[left] < pivot)) becomes
   \(\;\;\;\;\;\) while ((left <= right && aList[left] > pivot))
   and
   while ((right >= left && aList[right] > pivot)) becomes
   \(\;\;\;\;\;\) while ((right >= left && aList[right] < pivot))

Back to Questions