Quicksort#

The sorts we have seen previously, bubble sort, insertion sort, and selection sort all have a run-time that lies in \(\theta (n^2)\). Can we do better?

What would better look like? \(n^2 = n \cdot n\) so if we can get one of the \(n\) terms to grow slower we will have an improvement. Our goal is to find a faster sorting algorithm, one with a run-time in \(\theta(n \log n)\).

How might we create this algorithm? The simple sorts have one thing in common: only one item is put into its correct position with each major pass and the items do not move far from where they started. Could we create an algorithm that moves many items closer to their correct position, all in one pass? The answer is “yes” and many such algorithms have already been invented. We will study quicksort as it is one of the first such algorithms and it is easily expressed with recursion, so it provides an example of the usefulness of recursion. In particular, this usefulness includes increased writeability and readability.

Quicksort Algorithm#

In quicksort, we pick an item, called the pivot, in the list that will get positioned into its proper sorted place. We move all of the rest of the items so that those less than the pivot are placed into one set, called the lessor set and labeled as L, and those greater than the pivot are placed into another set called the greater set and labeled as G[1]. We then quicksort the lessor set and quicksort the greater set. Our fully sorted list is the result of sorting the lessor set, appended with the pivot, appended with the result of sorting the greater set, to get ascending order.

The algorithm consists of two parts: partitioning and sorting.

Algorithm partition(\(aList, aPivot\))
Assumes:
\(\;\;\;\;\;\) - items in \(aList\) are unique
\(\;\;\;\;\;\) - \(aPivot\) is out of \(aList\)
\(\;\;\;\;\;\) - L and G are empty to start

  1. For each item in aList:
    \(\;\;\;\;\;\) a. If the item is less than aPivot, move it into L
    \(\;\;\;\;\;\) b. Otherwise, move it into G

  2. Return the two lists L and G.

Algorithm quicksort(\(aList\))
Assumes:
\(\;\;\;\;\;\) - items in aList are unique

  1. Select a pivot and call it \(aPivot\)

  2. Remove the pivot from the list

  3. Partition \(aList\), i.e. {L, G} ← \(partition(aList, aPivot)\)

  4. Sort L to get L’:
    \(\;\;\;\;\;\) a. If L is empty or contains one element then L’ ← L
    \(\;\;\;\;\;\) b. Otherwise L’ ← \(quicksort\)(L)

  5. Sort G to get G’:
    \(\;\;\;\;\;\) a. If G is empty or contains one element then G’ ← G
    \(\;\;\;\;\;\) b. Otherwise G’ ← \(quicksort\)(G)

  6. Return the new list which is the combination of L’, {aPivot}, and G’, in that order

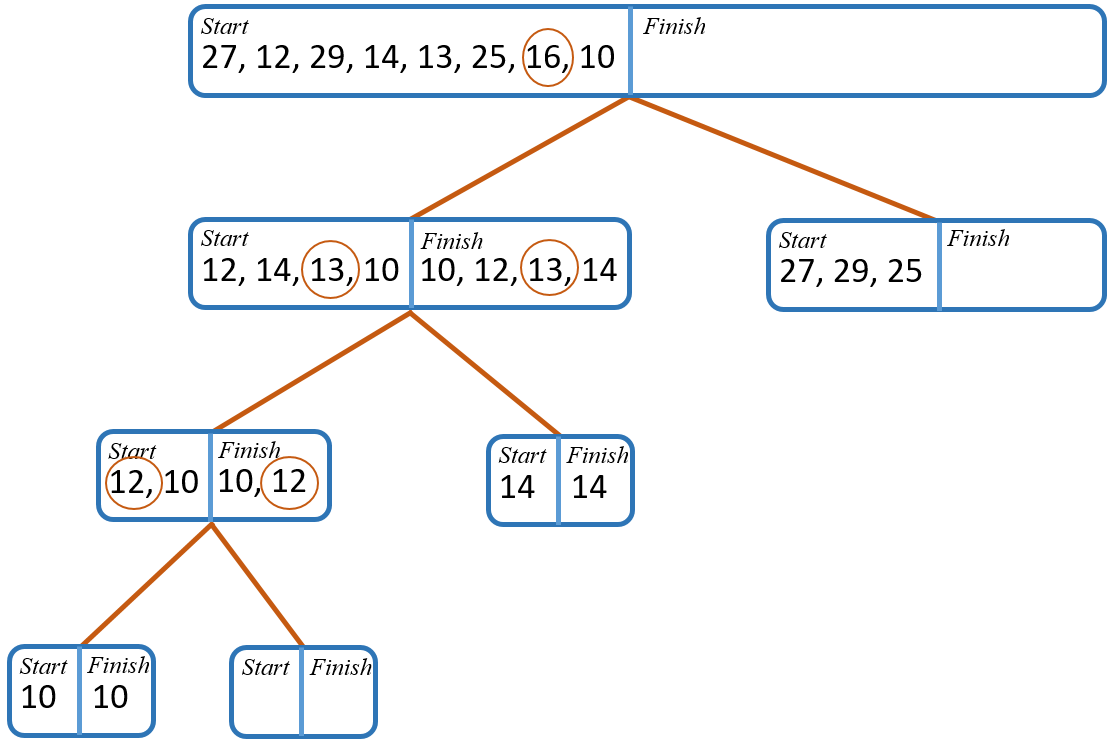
Quicksort Example#

This algorithm can be run on the following list:

{27, 12, 29, 14, 13, 25, 16, 10}

If the first pivot chosen is the 16, then when we partition, the lessor and greater sets are:

L1 = {12, 14, 13, 10}   the items less than 16
G1 = {27, 29, 25}       the items greater than 16

All the items in L1 will come before the pivot in our final sorted list; all the items in G1 will come after the pivot in our final sorted list.

Now quicksort is called on L1 and on G1. For L1, assume that the pivot chosen is 13. Then, when we partition, the new lessor and greater sets are:

L2 = {12, 10}
G2 = {14}

This requires one more call to quicksort, just on L2 as G2 is already sorted. If the pivot is 12, then the partition is:

L3 = {10}
G3 = {}

Putting this all together, by combining, creates this result so far:

quicksort(L1) + quicksort(G1)
{10, 12, 13, 14} + quicksort(G1)
quicksort half done



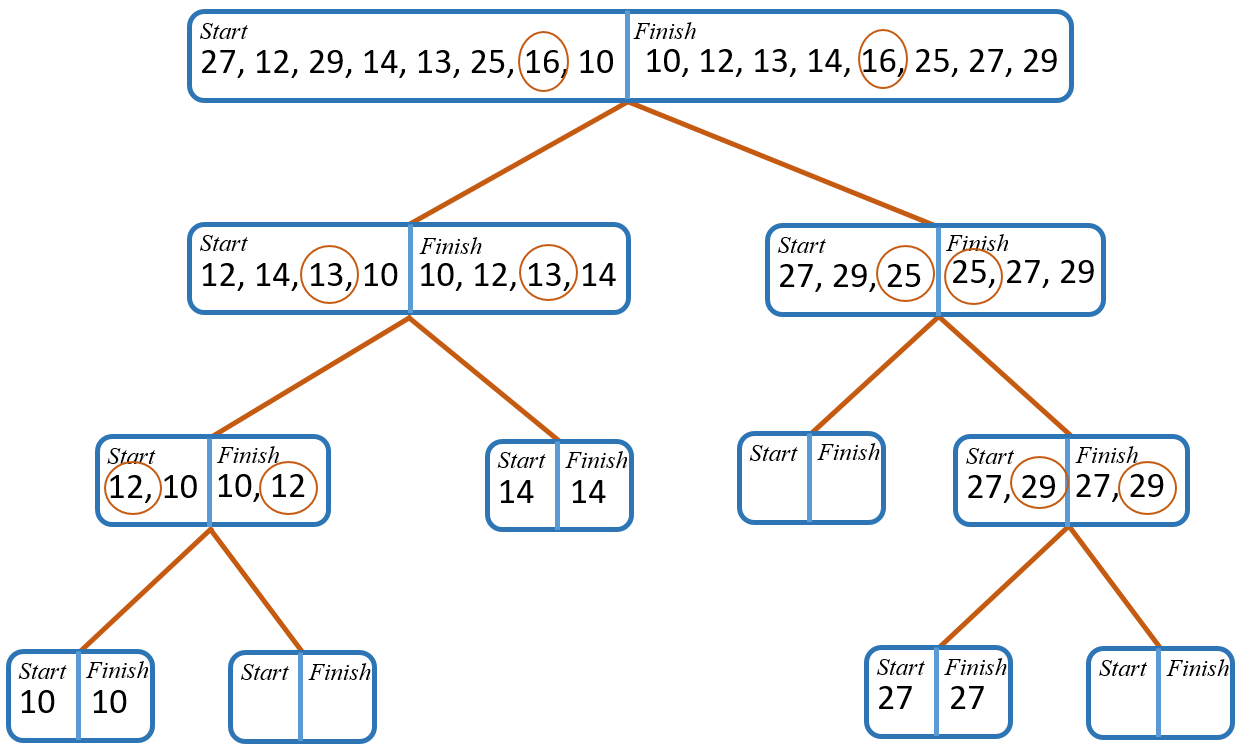
The algorithm is about half done. Now the G1 needs to be sorted. Partitioning G1, with pivot 25, yields:

L4 = {}
G4 = {27, 29}

One more call to quicksort, on G4 with pivot 29, will finish the process:

L5 = {27}
G5 = {}

Combining the results gives the final sorted list.

{10, 12, 13, 14} + quicksort(G1)
{10, 12, 13, 14} + {25, 27, 29}
{10, 12, 13, 14, 25, 27, 29}
quicksort all done

Quicksort Run-Time Complexity#

As you may see in the tree diagrams to the right, above, the first pass through the list results in one item in the correct place. The second pass results in two more items in the correct place, the two pivots. The third pass results in up to four more items in the correct place (three in our case because of the shortness of the list). This process continues, with each pass resulting in up to \(2^{p-1}\) more items in their correct place, where \(p\) is the pass number. We see an exponential growth in the number of items in the correct place with each pass through the list. Thus, we expect a logarithmic function as part of the run-time since there is an exponential amount less to do with each pass, that is run-time will be in \(\theta (n \log n)\).

We see that in this diagram, where the nodes at the end mark base cases and hence no key comparisons:

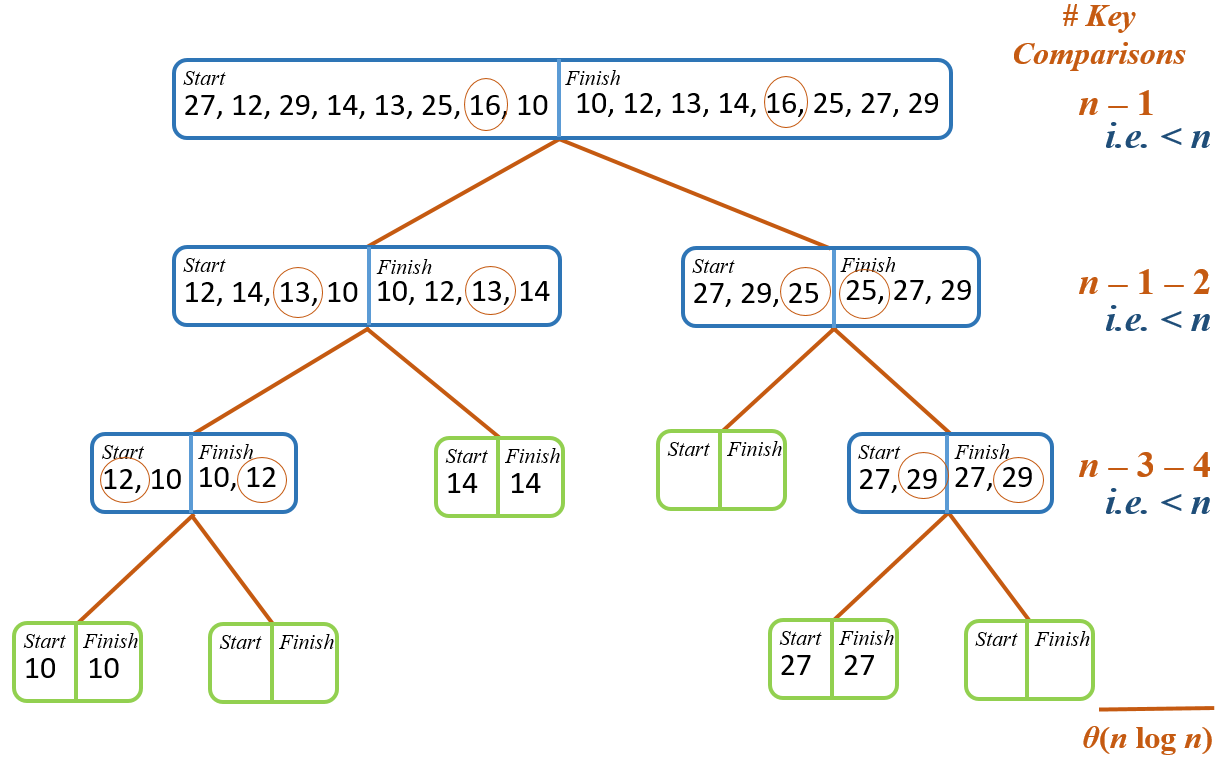
quicksort all done with complexity on right side

Each pass does fewer than \(n\) key comparisons to the pivot, significantly fewer as we move down the tree. The depth of the tree is a function of \(\log _2 n\), because we are cutting our list in about half each time, so our complexity result is in \(\theta (n \log n)\).

Note that this expectation of running in \(\theta (n \log n)\) is only valid if the input list keeps dividing approximately in half. There are cases where this will not happen, and we must be cautious.

Assumptions

Assumptions are critical in computing. We must overthink everything and see where those assumptions break down.

Worst Case Beware#

In the example above, the pivot was chosen to create the ideal situation for quicksort. However, in our programs, the pivot must be chosen in some pre-set manner, without knowing the input list. Suppose the pivot is chosen as the last item. What happens if our original list is exactly in order or in reverse order and we run quicksort?

Consider the initial list, to be sorted in ascending order:

{29, 27, 25, 16, 14, 13, 12, 10}

Here is a visualization of the process:

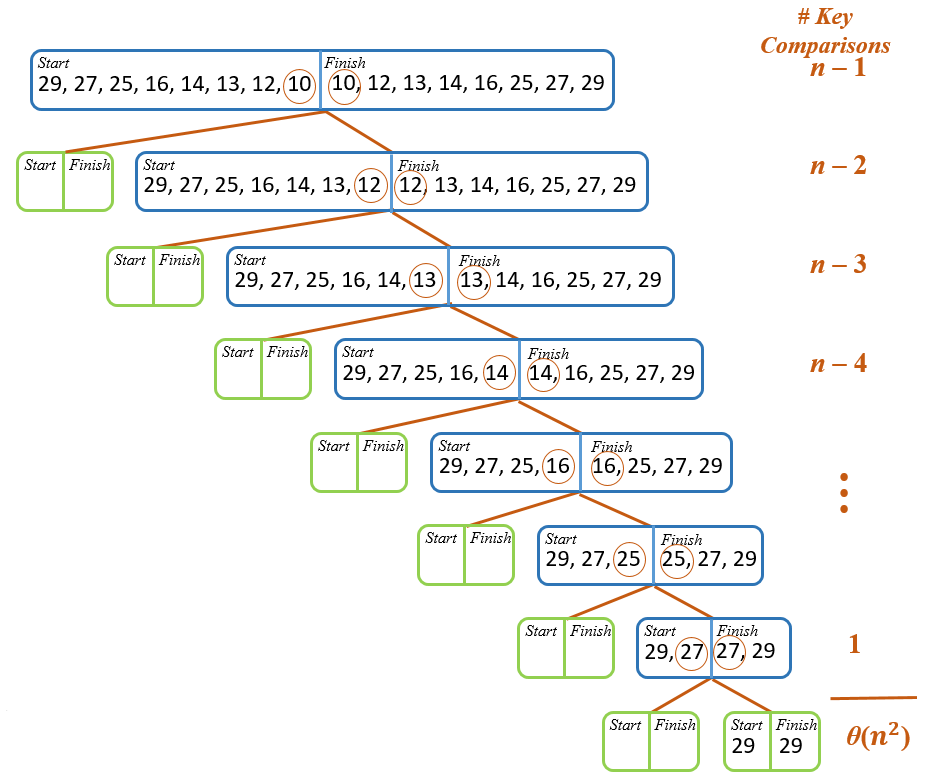
quicksort in worst case tree

Yikes! quicksort is back to an algorithm in \(\theta (n^2)\), no better than bubblesort. The run-time is even worse than bubblesort because we are making recursive calls and, thus, using the stack during execution.

However, though beyond the scope of this textbook, it has been shown that most of the time quicksort will run in \(\theta (n \log n)\) with a selection of a good pivot. A good pivot may be obtained by choosing the median of the first, middle, and last elements in the list. If we had done that in our previous example, we can see that our run-time is again in \(\theta (n \log n)\).

Programmer Beware Of Quicksort Worst Case

In life-critical, real-world applications, if no information is known about the data then quicksort must be treated as having run-time in \(\theta (n^2)\).

In-Place Quicksort#

Another potential problem with quicksort would be if the lessor and greater sets (L and G) are created with a copy process in memory. On a big list, there are three problems: the time required for allocation of the new memory, knowing the size of each list, and the computer may simply run out of memory.

Linked lists could be used to avoid these problems, but would require a lot of pointers to be moved. A single array can also be sorted directly in-place with quicksort, and require no extra memory. The idea is to put the pivot into a specific spot at the start, for example, at the end of the list. Think of the remainder of the list as divided into two sections: the left side will become L and the right side will become G. When partitioning is complete the pivot is moved to the middle by exchanging it with the first element of G.

Algorithm inPlacePartition(\(aList\), \(left\), \(right\))
Assumes:
\(\;\;\;\;\;\) - partitions the list between \(left\) and \(right\) inclusive
\(\;\;\;\;\;\) - items in \(aList\) are unique
\(\;\;\;\;\;\) - pivot is at location \(right + 1\) in \(aList\)

  1. Save variable \(pivotLoc\) ← \(right + 1\), need at the end when placing pivot

  2. Set \(aPivot\) ← \(aList[pivotLoc]\)

  3. REPEAT: As long as \(left <= right\), i.e. \(left\) and \(right\) have not crossed
    \(\;\;\;\;\;\) a. Find the first incorrect item in L, by moving \(left\) sequentially to it (forwards or towards the right)
    \(\;\;\;\;\;\) b. Find the first incorrect item in G, by moving \(right\) sequentially to it (backwards or towards the left)
    \(\;\;\;\;\;\) c. If \(left\) and \(right\) have not crossed:
    \(\;\;\;\;\;\)\(\;\;\;\;\;\) i. Swap the items at \(left\) and \(right\)
    \(\;\;\;\;\;\)\(\;\;\;\;\;\) ii. Increment \(left\)
    \(\;\;\;\;\;\)\(\;\;\;\;\;\) iii. Decrement \(right\)

  4. Place the pivot by swapping the items at \(pivotLoc\) and \(left\)

  5. Return \(left\) as that is now the location of the pivot. The L set is to the left of this location and the G set is to the right


Algorithm inPlaceQuicksort(\(aList\), \(left\), \(right\))
Assumes:
\(\;\;\;\;\;\) - sorts the list between \(left\) and \(right\) inclusive
\(\;\;\;\;\;\) - assumes the pivot is at \(right + 1\)
\(\;\;\;\;\;\) - items in \(aList\) are unique
\(\;\;\;\;\;\) - \(left\) and \(right\) are valid locations in the list, at least on first call

  1. Base Case: stop if \(left > right\)

  2. Partition and get new pivot location:
    \(\;\;\;\;\;\) \(pivotLoc\) ← \(inPlacePartition(aList, left, right)\)

  3. quicksort L with \(inPlaceQuicksort(aList, left, pivotLoc - 2)\)
    \(\;\;\;\;\;\) ” \(- 1\)” would take us to L, but the pivot is there so make boundary “\(- 2\)”

  4. quicksort G with \(inPlaceQuicksort(aList, pivotLoc + 1, right)\)

In-Place Quicksort Example#

Let’s see how inPlaceQuicksort works on this list:

{27, 12, 29, 14, 13, 25, 10, 16}

1 Starting configuration. \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\;\;\) \(\;\;\;\)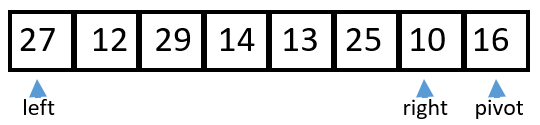

in place quicksort step 1. 27 12 29 14 13 25 10 16 left at 27 right at 10 pivot at 16

2 Neither 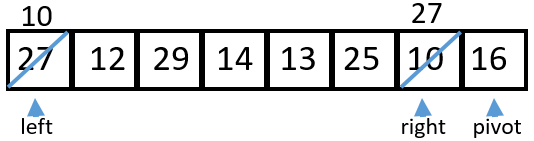left nor right move because each already has an item that needs to change. Items are swapped.

in place quicksort step 2. 10 12 29 14 13 25 27 16 left at 10 right at 27 pivot at 16

3 When swap is done, 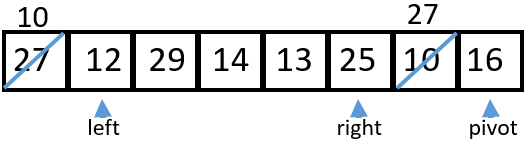left and right both move.

in place quicksort step 3. 10 12 29 14 13 25 27 16 left at 12 right at 25 pivot at 16

4 12 < 16 so 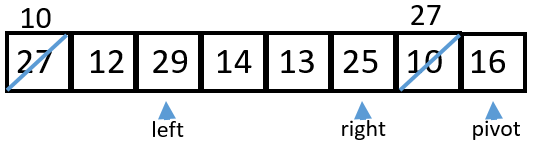left moves.

in place quicksort step 4. 10 12 29 14 13 25 27 16 left at 29 right at 25 pivot at 16

5 29 is not less than 16 so 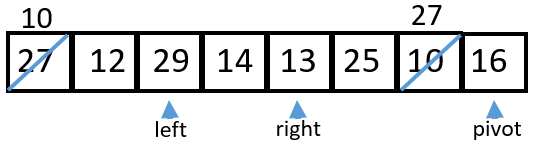left stops. 25 > 16 so right moves.

in place quicksort step 5. 10 12 29 14 13 25 27 16 left at 29 right at 13 pivot at 16

6 13 is not greater than 16 so 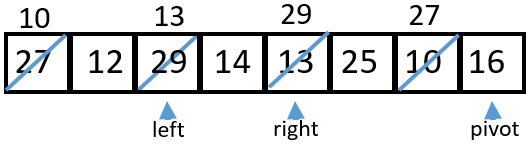right stops. Items at left and right are swapped.

in place quicksort step 6. 10 12 13 14 29 25 27 16 left at 13 right at 29 pivot at 16

7 After a swap, both 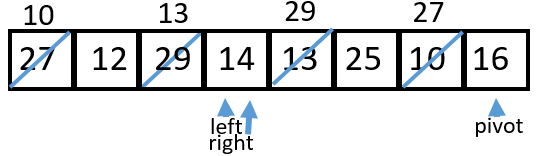left and right move.

in place quicksort step 7. 10 12 13 14 29 25 27 16 left at 14 right at 14 pivot at 16

8 14 < 16 so left moves. left and right have crossed.

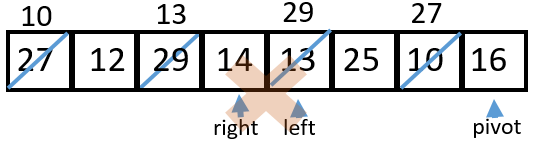
in place quicksort step 8. 10 12 13 14 29 25 27 16 left at 13 right at 14 pivot at 16

9 Swap pivot with left

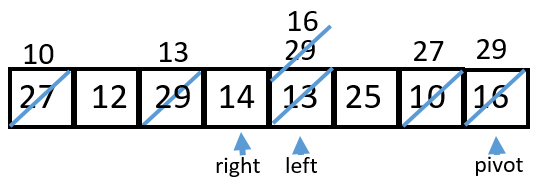
in place quicksort step 9. 10 12 13 14 16 25 27 29 left at 16 right at 14

10 Run inPlaceQuicksort on the lessor set and the greater set.

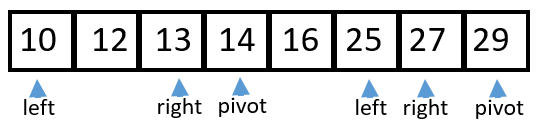
in place quicksort step 10. 10 12 13 14 16 25 27 29 left at 10 right at 13 pivot at 14 and left at 25 right at 27 pivot at 29

Do not assume the computer stops just because it looks to us like the list is sorted. The algorithm must run to completion, following the same steps on the two (sub)lists.

In-Place Quicksort Java Code#

Here is Java code for in-place quicksort:

/**
 * Swaps two items in an array of ints.
 * 
 * @param aList - the array
 * @param i - one location
 * @param j - other location
 * 
 * NOTE:  the array will be physically changed.
 */
private static void swap(int[] aList, int i, int j) {
    int temp = aList[i];
    aList[i] = aList[j];
    aList[j] = temp;
}

/**
 * In-place partitions a portion of an integer array for quicksort.
 * Assumes:
 * - unique items in aList
 * - pivot is at end of section to partition, i.e. location right + 1
 * 
 * @param aList - the array to partition
 * @param left - the starting location to partition
 * @param right - the ending location to partition
 * @return - the location of the pivot when done
 * 
 * NOTE:  the array will be physically changed. 
 */
private static int partition(int[] aList, int left, int right) {
    int pivotLoc = right + 1;
    int pivot = aList[pivotLoc];
    while (left <= right) {
        //Find first incorrect in L
        while ((left <= right && aList[left] < pivot)) {
            left++;
        }
        //Find first incorrect in G
        while ((right >= left && aList[right] > pivot)) {
            right--;
        }
        //Swap
        if (left < right) {
            swap(aList, left, right);
            left++;
            right--;
        }
    }

    //Place Pivot
    swap(aList, left, pivotLoc);

    //Need to know the boundary between L and G
    return left; 
}

//Uses the end item as the pivot
/**
 * Implements an in-place version of quicksort to sort a list of integers.
 * The last item in a section is assumed to be the pivot.
 * 
 * @param aList - the list to sort
 * 
 * NOTE 1: aList will be physically changed
 * NOTE 2: the items of aList must be unique
 * NOTE 3: this is a wrapper only
 */
public static void quicksort(int[] aList){
    //last item is at aList.length - 1 and that is the pivot
    //so sort only up to there (pivot moves into place by partition)
    quicksort(aList, 0, aList.length - 2);
}

/**
 * Actual recursive method for in-place quicksort.
 * 
 * @param aList - the array to sort
 * @param left - the lower bound for sort from (inclusive)
 * @param right - the upper bound to sort to (inclusive)
 * 
 * NOTE 1: the items of aList must be unique
 * NOTE 2: the pivot is the item at location right + 1
 */
private static void quicksort(int[] aList, int left, int right){
    int pivotLoc;

    //0 or 1 elements [if equality there are still 2 elements, this element
    //and the pivot, so equals is not included in the condition]
    if (left > right){ 
        return;
    }     

    pivotLoc = partition(aList, left, right);
    quicksort(aList, left, pivotLoc - 2);  //L (remember pivot at end)
    quicksort(aList, pivotLoc + 1, right); //G (new item moved to end)
}

Practice Questions#

  1. Draw the operation of inPlaceQuicksort, showing each pass, sorting in ascending order, on the following list:

    {24, 67, 102, 14, 90, 55, 10, 76, 92, 59}

    Identify all pivots.

  2. Draw the operation of inPlaceQuicksort, showing each pass, sorting in ascending order, on the following list:

    {7, 6, 5, 4, 3, 2, 1}

    Identify all pivots.

  3. Draw the operation of inPlaceQuicksort, showing each pass, sorting in ascending order, on the following list:

    {97, 68, 75, 34, 45, 60}

    Identify all pivots.

  4. Write a method called getMedianLoc that returns the location of the median of the first element, the last element, and the middle element of a list of integers. Assume that the list has three or more unique elements.

  5. Write a Java method to put the median of the first, middle, and last elements at the end of a list of integers and put the original last element wherever the median was. Use your method from the previous question. Assume that the list has three or more unique elements.

  6. What changes would need to be made to the in-place quicksort Java code if we wanted to sort the list in descending order?

To Solutions