Operations (Methods) for a Linked List

To complete any data type, including linked lists, we must write the methods or operations we will allow on linked lists. We will look at toString, insertion at the beginning, removal from the beginning, removal from the end, and insertion in the middle.

toString()

The algorithm to create a String representation from a linked list is:

Algorithm toString()

1. Start the representation at the empty string.
   

2. Start a cursor at the beginning of the linked list. This cursor will move through the list.
   

3. Create a loop – go one node at a time until we reach the end of the list and do this:
   \(\;\;\;\;\;\) a. Concatenate the value from the node to the representation.
   \(\;\;\;\;\;\) b. Move the cursor to the next node.
   

4. Return the representation.

The Java code is:

@Override
public String toString(){
   String repr = "";       //1.
   Node<V> cursor = head;  //2.
   
   while (cursor != null){ //3.
      repr = repr + cursor.getValue().toString() + " -> "; //a.
      cursor = cursor.getNext(); //b.
   }       
   return repr + "null";   //4.
}

Insertion at the Beginning (addFirst)

The algorithm to insert a new item at the beginning of the linked list is:

Algorithm addFirst(\(data\))

1. Allocate a new node in memory.
   

2. Put the data into the node (i.e. set the value).
   

3. Make the new node point to the head of the linked list.
   

4. Change the head of the linked list to the new node.
   

5. If this is the first node in the list, change the tail of the linked list to the new node.
   

6. Increase the size of the linked list.

In Java the code is: public void addFirst(V aValue) { Node<V> aNode = new Node(); //1. aNode.setValue(aValue); //2. aNode.setNext(head); //3. head = aNode; //4. if (size == 0){ //5. tail = aNode; } size++; //6. }

Visualization: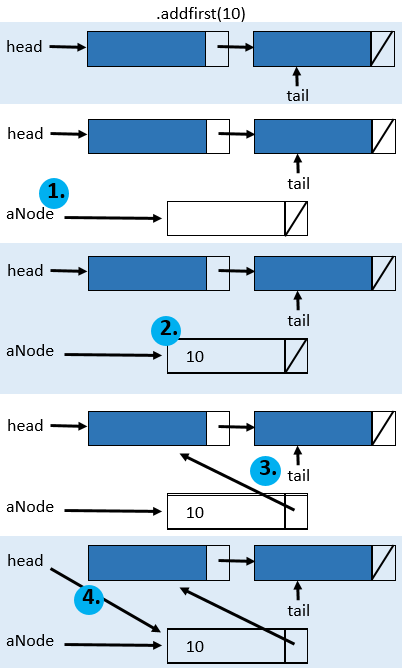

Note that steps 1-3 could all be combined in one line as:

Node<V> aNode = new Node(aValue, head);

Note also how important the order of the statements is. If we set head to aNode before connecting the new node into the list, then we will no longer have access to (the rest of) the linked list.

With these two methods, we can make the linked list that we made in the previous section. The Java code is:

LinkedList<String> names = new LinkedList<>();
names.addFirst("Tooth Fairy");
names.addFirst("Mickey Mouse");
names.addFirst("Santa Claus");

Here is a visualization for what this code has done:

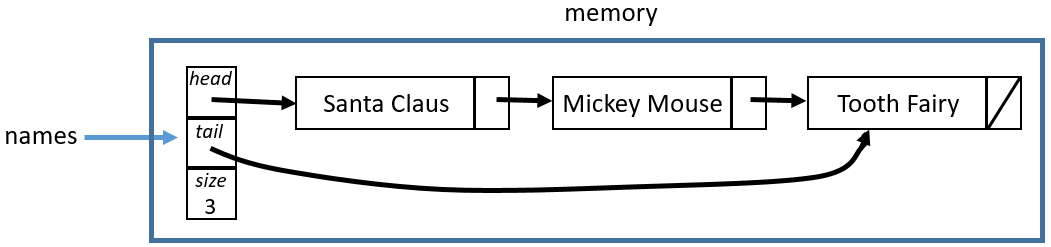
Removal From the Beginning, Returning Value (removeFirst)

The algorithm to remove from the beginning and return that value is:

Algorithm removeFirst()

1. If there is nothing in the list, just return null.
   

2. Label the first item (so we can later return its value).
   

3. Move the head of the list to the next item. Moving the head means that the list starts at what was the second item.
   

4. If the head is null, that means there was no next item. We must then set the tail to null too.

5. Decrement the size of the list.
   

6. Return the value saved by the label to the old first item.
   The garbage collector will “pick up” the node that can no longer be accessed, and make this memory space available again.

In Java the code is: public V removeFirst(){ if (size == 0){ //1. return null; } Node<V> temp = head; //2. head = head.getNext(); //3. if (head == null){ //4. tail = null; } size--; //5. return temp.getValue(); //6. }

Visualization: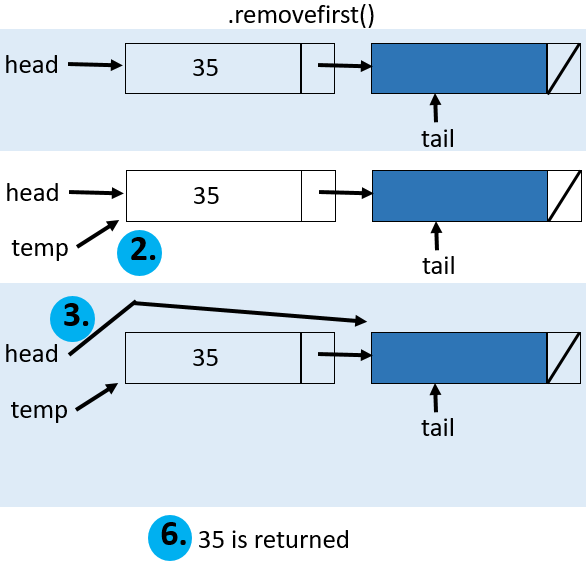

Removal From the End, Returning Value (removeLast)

The algorithm to remove from the end is much more complicated than removing from the beginning. Why is this? It is because we need to set the tail to the second last element and set the next field of the second last element to null. Those are easy operations, but the difficulty is finding where the second last element is. We cannot move backward in the list. Thus, we must move from the front of the list, through each node and look ahead to see if the next node is the tail. As soon as the next node is the tail, then we must stop moving as we have found the second last element. Here is the algorithm with more specific details:

Algorithm removeLast()

1. If there is nothing in the list, just return null.
   

2. Label the node to remove (i.e. the tail).
   

3. Start a cursor at the beginning of the list.
   

4. If the size of the list is 1, i.e. exactly one item, then to remove that item set head and tail to null.
   

5. If the size of the list is not 1
   \(\;\;\;\;\;\) a. Move through the list as long as the next item is not the tail.
   \(\;\;\;\;\;\) b. Set the second last node’s next field to null.
   \(\;\;\;\;\;\) c. Set the tail to the second last node.
   

6. Decrement size.
   

7. Return the value in the labeled node.

The garbage collector will “pick up” the node that can no longer be accessed, and make this memory space available again.

In Java the code is: public V removeLast(){ if (size == 0){ //1. return null; } Node<V> removeNode = tail; //2. Node<V> cursor = head; //3. if (size == 1){ //4. head = null; tail = null; } else{ //5. while (cursor.getNext() != tail){ //a. cursor = cursor.getNext(); } cursor.setNext(null); //b. tail = cursor; //c. } size--; //6. return removeNode.getValue(); //7. }

Visualization: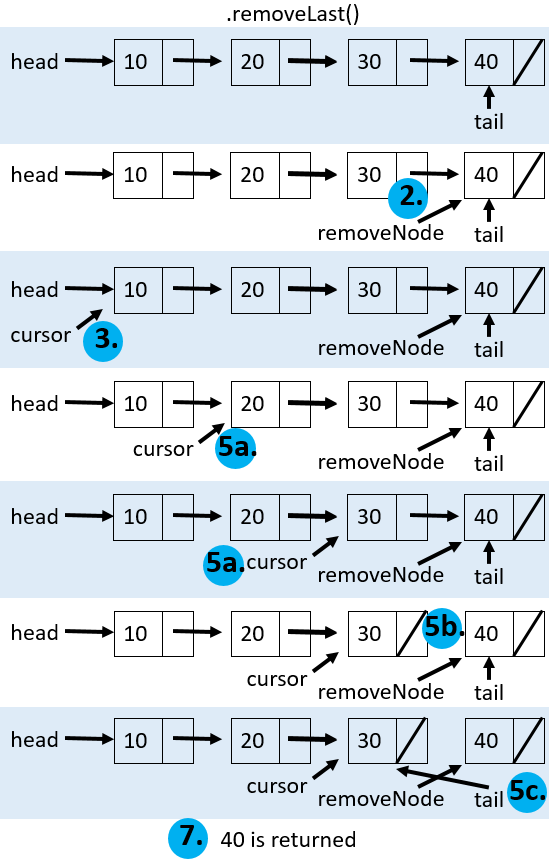

Notice, in particular, that removing the last node requires a time of \(θ(n)\), when \(n > 1\), since we must move through the entire list (minus the last node) looking for the second last node, essentially a sequential search. Removing from the beginning was done in constant time.

Insertion in the Middle

We must find the node to insert after. In the case of an even-sized list, the middle is clear and occurs right after the \(\frac{size}{2}\)th node. Let’s use the same calculation to find the middle of an odd-sized list, so the item will be placed to the left of the middle item. We must find where in the list to perform the insertion. This will be a form of sequential search, moving past half of the items in the list. Here is the algorithm:

Algorithm addInMiddle(\(value\))

1. Make a new node with the given value and set the next field to null.

2. If the size of the list is 0, just set the head and the tail to this new node.

3. Otherwise, if the size of the list is not 0:
   \(\;\;\;\;\;\) a. Make a counter to start at 1.
   \(\;\;\;\;\;\) b. Make a cursor to start at the head.
   \(\;\;\;\;\;\) c. Move the cursor the correct number of times (half of the size).
   \(\;\;\;\;\;\) d. Set the new node’s next field to the node after the cursor.
   \(\;\;\;\;\;\) e. Set the cursor’s next field to the new node.

4. Increment the size of the list.

Here is the Java code:

public void addInMiddle(V aValue) {
   Node<V> aNode = new Node(aValue);  //1.
   if (size == 0){                    //2.
      head = aNode;
      tail = aNode;
   }
   else{                              //3.
       int countNodes = 1;               //a.
       Node<V> cursor = head;            //b.
       
       while (countNodes < size / 2){    //c.
           cursor = cursor.getNext();
           countNodes++;
       }//while
       
       aNode.setNext(cursor.getNext());   //d.
       cursor.setNext(aNode);             //e.
   }//else
   
   size++;                             //4.
}

With the sequential search component, we can see that the time complexity is in \(θ(n)\), for non-trivial values of \(n\).

Practice Questions

1. Make a linked list containing your five most favorite foods, one food per node. Print the list.

2. Make a linked list containing your courses from this semester and the corresponding mark, one node per course. Print the list.

3. Write a method that takes a linked list with values that are of type Integer and returns their average as a double.

4. Write the Java code to insert a new node with a given value at the end of a linked list. This code would go inside the LinkedList class.

5. Write the Java code to insert a new node with a given value right after a node that has a specific value. Print an error message if the specific value is not in the list. This code would go inside the LinkedList class.

To Solutions