Example - Sum an Array with Both Loop and Recursion#
Suppose that we want to sum an array of integers. The most likely way to do that is to create a simple loop, moving through the array from item to item and adding each to the sum. The code might look something like this:
public static int sumArray(int[] anArray){
int sum = 0;
for (int i = 0; i < anArray.length; i++){
sum = sum + anArray[i];
}
return sum;
}
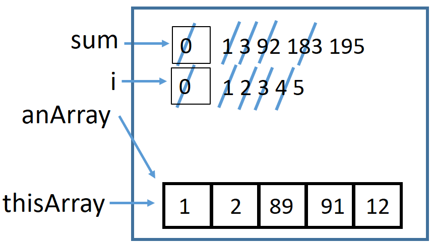
If we run sumArray(thisArray) where thisArray is
{1, 2, 89, 91, 12}
then the result is 195. A memory diagram of running sumArray(thisArray) is:
sumArray With Recursion#
Now let’s do the same thing with recursion – making a method that calls itself to find the same sum. Just as when we are making a loop, we will need to control the location from which to add to the sum. Local variables will not be helpful with this control, because they are made new each time on the stack as the method is called recursively. Rather, control comes through a parameter to the method. Each recursive call will update this parameter. The code might look like this:
public static int sumArray(int[] anArray, int loc){
if (loc >= anArray.length){
return 0;
}
return anArray[loc] + sumArray(anArray, loc + 1);
}
If we run the method call as we did in the loop example, except now adding our starting location, we will obtain the same result of 195. Our method call would be:
sumArray(thisArray, 0)
Visualization of Recursive sumArray#
Using a stack trace, this is how the recursive code works:
1 Call 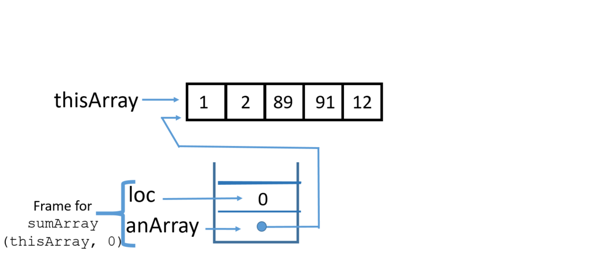
|
2 Call 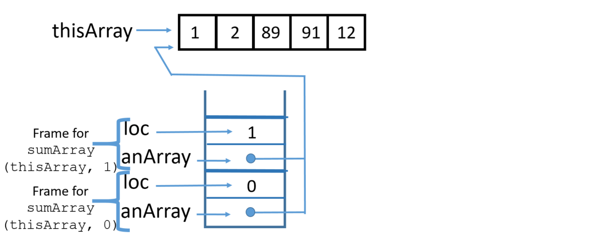
|
3 Call 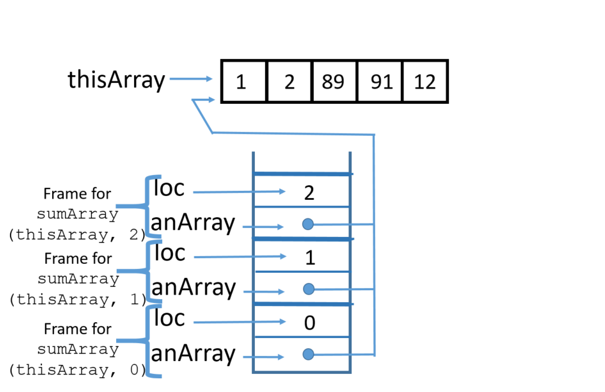
|
4 Call 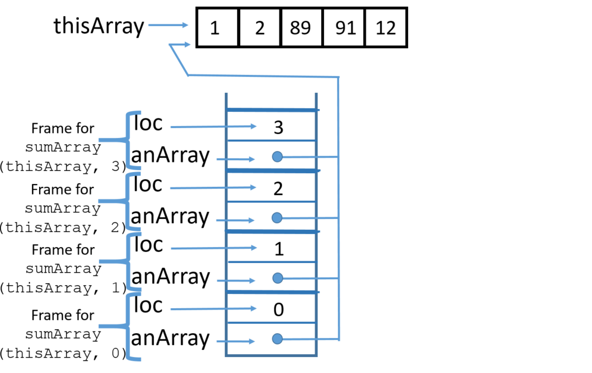
|
5 Call 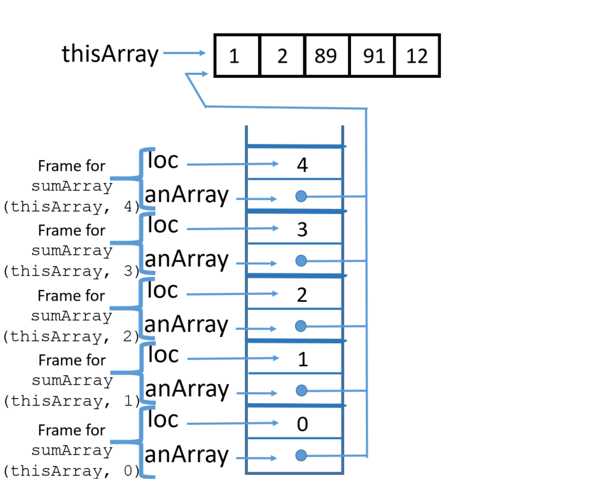
|
6 Call 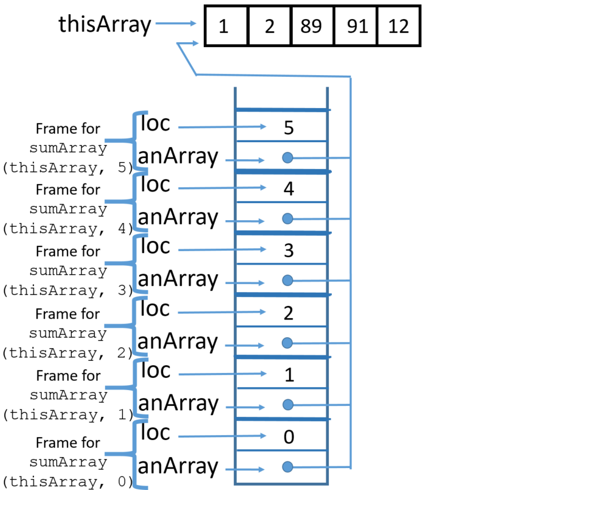
|
7 Return from 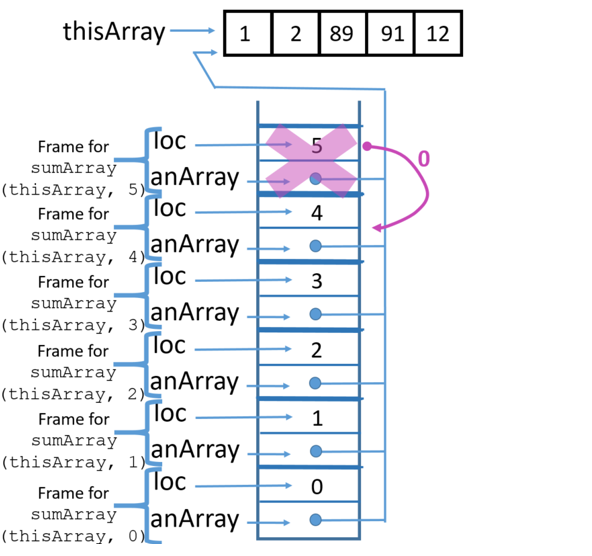
|
8 Return from 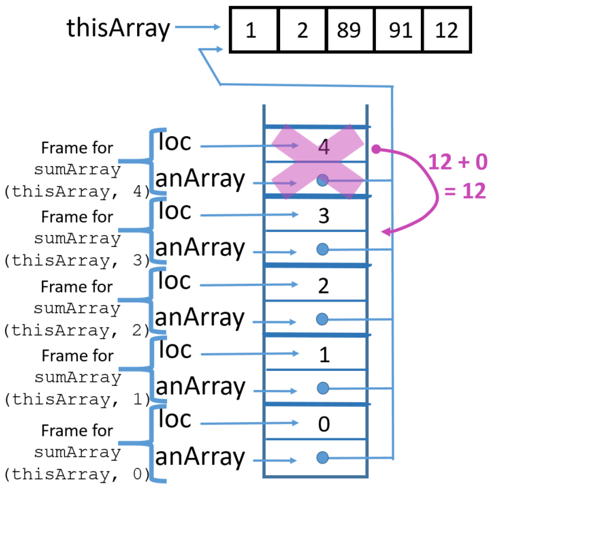
|
9 Return from 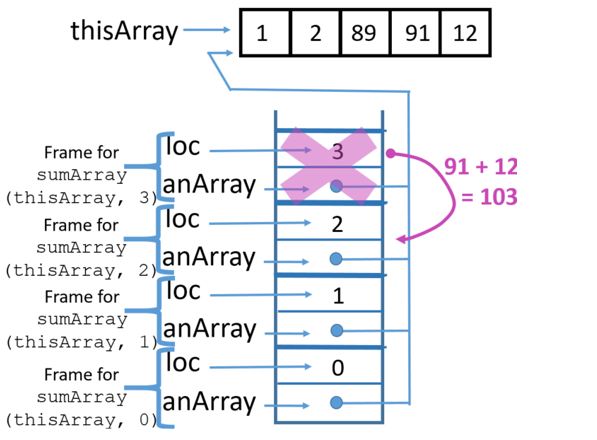
|
10 Return from 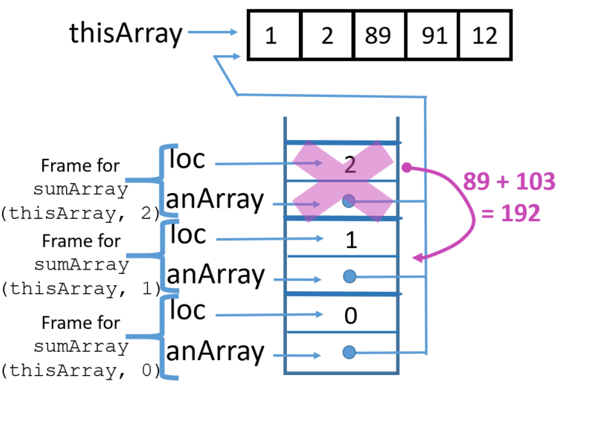
|
11 Return from 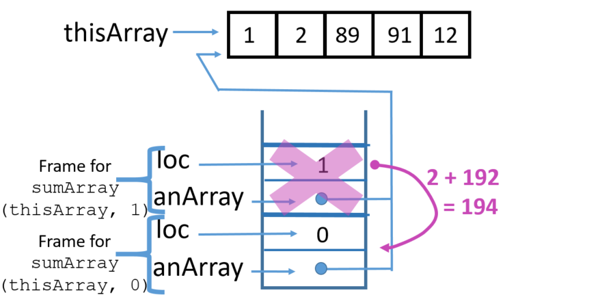
|
12 Return from 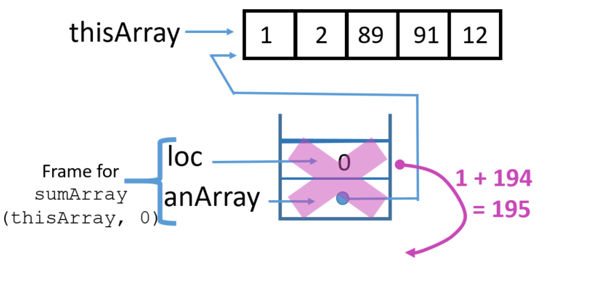
|
Maintain the Desired Signature with a Wrapper#

Often we want to maintain the same signature on our recursive method as we would have on our method with the loop. We do not want to be forced to remember to send the starting location along on our method call. We can get our original signature back by writing a wrapper method. This is much like a birthday gift with wrapping paper, the superficial looks, around the actual gift, the item of worth[1].
Our wrapper method simply calls the recursive method, with the location initialized. We could use the same name for both methods (wrapper and worker) because they have unique signatures. However, I have renamed the recursive method with a name that has Sub appended to make it clear that it is subordinate and the other should be used. I’ve also made the subordinate method private, again to indicate that it is not intended to be called directly from elsewhere.
public static int sumArray(int[] anArray){
return sumArraySub(anArray, 0); //Call to recursive method, with location parameter initialized
}
private static int sumArraySub(int[] anArray, int loc){
if (loc >= anArray.length){
return 0;
}
return anArray[loc] + sumArraySub(anArray, loc + 1);
}
Null Arrays#
Our code above will not work on an array that is null, that is, which is not yet created. Wrappers can be a great place to take care of this situation, eliminating the exception that would otherwise occur because a null object cannot respond to any dot messages. If we want the sum of a null array to be zero, we would modify our wrapper as follows:
public static int sumArray(int[] anArray){
if (anArray == null){
return 0;
}
return sumArraySub(anArray, 0);
}
Tail Recursion#
Solving a problem using recursion versus using a loop results in a slower run-time because of the substantial use of the system stack. Nevertheless, we use recursion to enhance readability, writeability, and expressivity. It is sometimes faster to write a solution using recursion and is often easier to read because the code is shorter. It turns out that a certain kind of recursion may be translated into a loop algorithmically. This means we can write our code with recursion but still have the fast run time of a loop once the compiler has translated our code to machine language.
The kind of recursion required for this speed-up is tail-recursion, which means that the recursive call is the last thing done by a recursive method not including any base case calculations. In the backward trek, as the stack frames are popping off, only a value is passed along and no further work is done in the method. A frequent “trick” to make a method tail recursive is to build up the result in a parameter and use a wrapper to initialize that result.
In sumArray above, notice that the last thing that always needs to be done is the addition operation. When popping off the stack, the computer adds the value from the higher recursive level to the value in the array at the current location. This situation is not tail-recursive. The method would be tail-recursive if the recursive call stands alone as the last action that is done before a base case is reached. Let’s use the technique of adding a parameter to make this method tail-recursive. The extra parameter sum will hold our result as the sum is built.
public static int sumArrayTR(int[] anArray){
if (anArray == null){
return 0;
}
return sumArrayTRSub(anArray, 0, 0);
}
private static int sumArrayTRSub(int[] anArray, int loc, int sum){
if (loc >= anArray.length){
return sum;
}
return sumArrayTRSub(anArray, loc + 1, sum + anArray[loc]);
}
With each recursive call, we build our sum in the 3rd parameter. When we reach the base case, all our work is done and we simply return the sum that we built. This sum is returned to each stack frame below, as the current frame is popped. No further work is done. This is tail-recursive.
Practice Questions#
What is the base case in
sumArrayTRSub?How does the recursive call in
sumArrayTRSubmove towards base case?Suppose
myArray = {5, -3, 8}. Draw the stack frames for the execution ofsumArrayTRSub(myArray, 0, 0).Suppose
myArray = {5, -3, 8}. Draw the stack frames for the execution ofsumArrayTRSub(myArray, 2, 0). Note: the second parameter here is different from the previous question.
