Coulomb Scattering of Electrons

Consider Rutherford scattering of an electron from a fixed Coulomb potential (figure 7.2).

Figure 7.2: Scattering of an electron from a fixed Coulomb potential.

The $S$-matrix is

$$S_{fi} = -ie\int d^4x \overline{\psi}_f(x) \not{\!\!A}(x) \Psi_i(x) \quad (f\ne i).$$ (7.26)

In lowest order the wavefunctions reduce to plane waves:

$$\psi_i(x) = \sqrt{\frac{m}{E_iV}} u(p_i,s_i) e^{-ip_i\cdot x} ,$$ (7.27)

$$\overline{\psi}_f(x) = \sqrt{\frac{m}{E_fV}} \overline{u}(p_f,s_f) e^{ip_f\cdot x} ,$$ (7.28)

where we have normalized to unit probability in a box of volume $V$.

The Coulomb potential is

$$A_0(x) = \frac{-Ze}{4\pi\vert\vec{x}\vert} \quad\textrm{and}\quad \vec{A}(x) = 0 .$$ (7.29)

We are working in the Heaviside-Lorentz (rationalized Gaussian) system of units. If we were working in the Gaussian system of units, the Coulomb potential would be $A_0(x) = -Ze/\vert\vec{x}\vert$. Thus

$$S_{fi} = \frac{iZe^2}{4\pi} \frac{1}{V} \sqrt{\frac{m^2}{E_fE_i}} \overlin... ...) \gamma^0 u(p_i,s_i) \int \frac{d^4x}{\vert\vec{x}\vert} e^{i(p_f-p_i)\cdot x}$$

$$= \frac{iZe^2}{2V} \sqrt{\frac{m^2}{E_fE_i}} \overline{u}(p_f,s_f) ... ... \int \frac{d^3x}{\vert\vec{x}\vert} e^{-i(\vec{p}_f-\vec{p}_i)\cdot \vec{x}} .$$ (7.30)

The space integral is the Fourier transform of the Coulomb potential

$$\int \frac{d^3x}{\vert\vec{x}\vert} e^{-i\vec{q}\cdot\vec{x}} = \frac{4\pi}{\vert\vec{q}\vert^2} ,$$ (7.31)

where $\vec{q}=\vec{p}_f-\vec{p}_i$. Therefore

$$S_{fi} = \frac{2i\pi Ze^2}{V} \sqrt{\frac{m^2}{E_fE_i}} \fra... ...) \gamma^0 u(p_i,s_i)}{\vert\vec{q}\vert^2} \delta(E_f-E_i) .$$ (7.32)

The number of final states in the momentum interval $d^3p_f$ is $V\frac{d^3p_f}{(2\pi)^3}$. To see this we notice that standing waves in a cubic box of volume $V=L^3$ require

$$k_x L = 2 \pi n_x ,$$

$$k_y L = 2 \pi n_y ,$$

$$k_z L = 2 \pi n_z ,$$ (7.33)

with integer numbers $n_x,n_y,n_z$. For large $L$ the descrete set of $\vec{k}$-values approaches a continum. The number of states is (setting $\hbar=1$)

$$dN = dn_x dn_y dn_y ,$$

$$= \frac{1}{(2\pi)^3} L^3 dk_x dk_y dk_y ,$$

$$= \frac{V}{(2\pi)^3} d^3k .$$ (7.34)

The transition probability per particle into these states is

$$\vert S_{fi}\vert^2V\frac{d^3p_f}{(2\pi)^3} = \frac{Z^2(4\pi... ...\vert^4} \frac{d^3p_f}{(2\pi)^3E_f} [2\pi\delta(E_f-E_i)]^2 .$$ (7.35)

The square of the $\delta$-function is mathematically not well defined, it is a divergent quantity and has to be specified by a limiting procedure. We can reason it to be

$$[2\pi\delta(E_f-E_i)]^2 = \lim_{T\rightarrow\infty} \int^{T/2}_{-T/2} dt e^{i(E_f-E_i)t} 2\pi \delta(E_f-E_i) .$$ (7.36)

If $E_f=E_i$, as required by the other remaining delta function, then

$$2\pi\delta(E_f-E_i) = \lim_{T\rightarrow\infty} \int^{T/2}_{-T/2} dt e^{i(E_f-E_i)t} .$$ (7.37)

For $E_f = E_i$,

$$2\pi\delta(0) = \lim_{T\rightarrow\infty} \int_{-T/2}^{T/2} dt = T$$ (7.38)

and

$$[2\pi\delta(E_f-E_i)]^2 = 2\pi T\delta(E_f-E_i) .$$ (7.39)

Another way of viewing this is that the finite time interval smears the delta-function

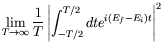$$\lim_{T\rightarrow\infty} \frac{1}{T} \left\vert \int^{T/2}_{-T/2} dt e^{i(E_f-E_i)t} \right\vert^2 = \lim_{T\rightarrow\infty} \frac{1}{T} \left[ \frac{\sin(E_f-E_i)T/2}{(E_f-E_i)/2} \right]^2 ,$$

$$= \frac{2\pi\delta(E_f-E_i)}{T} .$$ (7.40)

Using wave-packets instead of plane waves removes the need to square the delta-function.

If we consider transitions in a time $T$ and divide out the time, we obtain the rate, which is the number $R$ of transitions per unit time into momentum interval $d^3p_f$:

$$R = \vert S_{fi}\vert^2 \frac{V}{T} \frac{d^3p_f}{(2\pi)^3} ... ...^2}{\vert\vec{q}\vert^4} \frac{d^3p_f}{E_f} \delta(E_f-E_i) .$$ (7.41)

A cross-section is defined as the transition rate $R$ divided by the flux of incident particles $J_{inc}^a = \overline{\psi}_i(x)\gamma^a\psi_i(x)$, where $a$ denotes the vector component along the incident velocity $\vec{v}_i=\vec{p}_i/E_i$. With the normalization we have adapted, the flux is

$$\vert J_{inc}\vert = \frac{m}{EV}u_i^\dagger\alpha u_i = \fr... ...rac{\vert\vec{p}_i\vert}{m} = \frac{\vert\vec{v}_i\vert}{V} .$$ (7.42)

Thus the differential cross-section, $d\sigma$, per unit solid angle, $d\Omega$, is

$$\frac{d\sigma}{d\Omega} = \frac{R}{J^a_{inc}} = \int \frac{4... ...{\vert\vec{q}\vert^4} \frac{p_f^2dp_f}{E_f} \delta(E_f-E_i) .$$ (7.43)

Since $p_fdp_f=E_fdE_f$, we obtain

$$\frac{d\sigma}{d\Omega} = 4Z^2\alpha^2m^2 \int \frac{\vert\overline{u}(p_f,s_f) \gamma^0 u(... ...q}\vert^4} dE_f \frac{\vert\vec{p_f}\vert}{\vert\vec{p_i}\vert} \delta(E_f-E_i)$$

$$= \frac{4Z^2\alpha^2m^2}{\vert\vec{q}\vert^4} \vert\overline{u}(p_f,s_f) \gamma^0 u(p_i,s_i)\vert^2,$$ (7.44)

which is the Rutherford scattering cross-section in the non-relativistic limit.

In general, one does not know the initial polarizations so we average over these. Also, one does not observe the final polarization so we sum over these.

$$\frac{d\overline{\sigma}}{d\Omega} = \frac{4Z^2\alpha^2m^2}... ... s_i} \vert\overline{u}(p_f,s_f) \gamma^0 u(p_i,s_i)\vert^2 .$$ (7.45)

It is important to note that this is an incoherent average, in the sense that we average the cross-section, rather than the amplitude.

Consider the spin sum

$$\sum_{\pm s_f,\pm s_i} \overline{u}_\alpha(p_f,s_f) \gamma^0_{\al... ...^0_{\lambda\delta})^\dagger (\gamma^0_{\delta\sigma})^\dagger u_\sigma(p_f,s_f)$$

$$= \sum_{\pm s_f,\pm s_i} \overline{u}_\alpha(p_f,s_f) \gamma^0_{\al... ..._i,s_i) \overline{u}_\delta(p_i,s_i) \gamma^0_{\delta\sigma} u_\sigma(p_f,s_f).$$ (7.46)

We remember

$$u_\alpha(p,s)\overline{u}_\beta(p,s) + u_\alpha(p,-s)\overli... ... v_\alpha(p,-s)\overline{v}_\beta(p,-s) = \delta_{\alpha\beta}$$ (7.47)

and notice that operating with $\Lambda_+(p)$, we have

$$u_\alpha(p,s)\overline{u}_\beta(p,s) + u_\alpha(p,-s)\overline{u}_\beta(p,-s) = [\Lambda_+(p)]_{\alpha\beta}$$

$$\sum_{\pm s} u_\alpha(p,s)\overline{u}_\beta(p,s) = [\Lambda_+(p)]_{\alpha\beta} .$$ (7.48)

The spin sum (eqaution 7.46) thus becomes

$$\sum_{\pm s_f} \overline{u}_\alpha(p_f,s_f) \left( \gamma^0 ... ... \left( \frac{\not{\;\!\!\!p}_f+m}{2m} \right)_{\beta\alpha} ,$$ (7.49)

which is a trace. Therefore

$$\frac{d\overline{\sigma}}{d\Omega} = \frac{4Z^2\alpha^2m^2}{... ...!p}_i+m}{2m} \gamma_0 \frac{\not{\;\!\!\!p}_f+m}{2m} \right] .$$ (7.50)

Using trace theorems we have

$$\textrm{Tr} \left[ \gamma_0 \frac{\not{\;\!\!\!p}_i+m}{2m} \gamma_0 \frac{\not{\;\!\!\!p}_f+m}{2m} \right] = \frac{1}{4m^2} \left( \textrm{Tr} [\gamma_0\not{\;\!\!\!p}_i\gamma_0\not{\;\!\!\!p}_f] + m^2 \textrm{Tr} [(\gamma_0)^2] \right)$$

$$= \frac{1}{m^2} \left(p_i^0 p_f^0 + p_f^0 p_i^0 - p_i\cdot p_f + m^2 \right)$$

$$= \frac{1}{m^2} \left(2E_i E_f - p_i\cdot p_f + m^2 \right)$$ (7.51)

and

$$\frac{d\overline{\sigma}}{d\Omega} = \frac{2Z^2\alpha^2}{\vert\vec{q}\vert^4} \left( 2E_iE_f - p_i\cdot p_f + m^2 \right).$$ (7.52)

The differential cross-section can be written in terms of the scattering energy, $E$, and scattering angle, $\theta$. Since $E = E_i = E_f$, $\vert\vec{p}\vert = \vert\vec{p}_i\vert = \vert\vec{p}_f\vert$, but $\vec{p}_i \ne \vec{p}_f$. The kinematical relations become

$$p_i\cdot p_f = E^2 - \vec{p}^{\ 2} \cos\theta$$

$$= m^2 + \vec{p}^{\ 2}(1 - \cos\theta)$$

$$= m^2 + 2\beta^2 E^2\sin^2\frac{\theta}{2}$$ (7.53)

and

$$\vert\vec{q}\vert^2 = \vert\vec{p}_f-\vec{p}_i\vert^2$$

$$= 2\vec{p}^{\ 2} - 2\vec{p}_f\cdot\vec{p}_i$$

$$= 2\vec{p}^{\ 2} ( 1 - \cos\theta)$$

$$= 4\vec{p}^{\ 2} \sin^2 \frac{\theta}{2} .$$ (7.54)

We find

$$\fbox{$\displaystyle \frac{d\overline{\sigma}}{d\Omega} = \f... ...ta/2)} \left( 1 - \beta^2 \sin^2\frac{\theta}{2} \right) $}\ .$$ (7.55)

This is the Mott cross-section. It reduces to the Rutherford formula as $\beta\rightarrow 0$. Which agrees with the non-relativistic Born approximation for the scattering amplitude

$$f_{p_i}(\theta) = \frac{m}{2\pi} \int d^3r e^{-\vec{q}\cdot\... ...rt\vec{q}\vert^2} = \frac{mZ\alpha}{2p_i^2\sin^2(\theta/2)} .$$ (7.56)