Theorem 6

$$\textrm{Tr}[\not{\;\!\!a}_1\not{\;\!\!a}_2\cdots\not{\;\!\!a... ...}[\not{\;\!\!a}_{2n} \cdots \not{\;\!\!a}_2\not{\;\!\!a}_1] .$$ (7.74)

Poof: From the charge conjugation discussion, recall that there exists a matrix $C$ such that $C\gamma_\mu C^{-1}=-\gamma_\mu^T$. Then

$$\textrm{Tr}[\not{\;\!\!a}_1\not{\;\!\!a}_2\cdots\not{\;\!\!a}_{2n}] = \textrm{Tr}[C\not{\;\!\!a}_1C^{-1}C\not{\;\!\!a}_2C^{-1}\cdots C\not{\;\!\!a}_{2n}C^{-1}]$$

$$= (-1)^{2n}\textrm{Tr}[\not{\;\!\!a}_1^T\not{\;\!\!a}_2^T\cdots\not{\;\!\!a}_{2n}^T]$$

$$= \textrm{Tr}[\not{\;\!\!a}_{2n}\cdots\not{\;\!\!a}_2\not{\;\!\!a}_1]^T$$

$$= \textrm{Tr}[\not{\;\!\!a}_{2n}\cdots\not{\;\!\!a}_2\not{\;\!\!a}_1] .$$ (7.75)

A general from which we shall often encounter is

$$\vert\overline{u}(f)\Gamma u(i)\vert^2 = \vert u^\dagger(f) \gamma^0 \Gamma u(i)\vert^2 ,$$

$$= [u^\dagger(f) \gamma^0 \Gamma u(i)][u^\dagger(i) \Gamma^\dagger (\gamma^0)^\dagger u(f)] ,$$

$$= [\overline(f) \Gamma u(i)][\overline{u}(i) \gamma^0 \Gamma^\dagger \gamma^0 u(f)] ,$$

$$= [\overline(f) \Gamma u(i)][\overline{u}(i) \overline{\Gamma} u(f)] ,$$ (7.76)

where $\overline{\Gamma} = \gamma^0\Gamma^\dagger\gamma^0$, and $\Gamma$ is some combination of Dirac matrices.

For

$$\overline{\gamma^\mu} = \gamma^0 (\gamma^\mu)^\dagger \gamma^0 = \gamma^\mu$$

$$\overline{i\gamma^5} = \gamma^0 (i\gamma^5)^\dagger \gamma^0 = i\gamma^5$$

$$\overline{\gamma^\mu\gamma^5} = \gamma^0 (\gamma^5)^\dagger (\gamma^\mu)^\dagger \gamma^0 = \gamma^\mu\gamma^5$$

$$\overline{\not{\;\!\!a}\not{b}\not{c}\cdots\not{p}} = \gamma^0 \not{p}^\dagger \cdots \not{c}^\dagger \not{b}^\dagger \not{\;\!\!a}^\dagger \gamma^0 = \not{p}\cdots\not{c}\not{b}\not{\;\!\!a}.$$ (7.77)

We often encounter the form

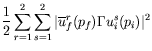$$\frac{1}{2} \sum_{r=1}^2 \sum_{s=1}^2 \vert\overline{u}_f^r(p_f) \Gamma u_i^s(p_i)\vert^2$$ (7.78)

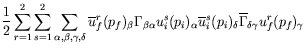$$\noindent = \frac{1}{2} \sum_{r=1}^2 \sum_{s=1}^2 \sum_{\alpha,\beta,\gamma,\... ...\overline{u}_i^s(p_i)_\delta \overline{\Gamma}_{\delta\gamma} u_f^r(p_f)_\gamma$$ (7.79)

$$= \frac{1}{2} \sum_{\alpha,\beta,\gamma,\delta} \Gamma_{\beta\alpha... ...mma}_{\delta\gamma} \left( \frac{\not{\;\!\!\!p}_f+m}{2m} \right)_{\gamma\beta}$$

$$= \frac{1}{8m^2} \textrm{Tr}[ \Gamma(\not{\;\!\!\!p}_i+m)\overline{\Gamma}(\not{\;\!\!\!p}_f+m)]$$

The other ``trick'' we will use is to introduce the unit 4-vector, $a$ with a 1 in the component 0 to put $\gamma^0$ into the slash notation. The other components are zero: $a = (1,0,0,0)$.