Coulomb Scattering of Positrons

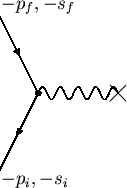
We now consider the scattering of positrons in a Coulomb field. We expect the form to be similar to the Coulomb scattering of an electron.

Figure 7.3: Coulomb scattering of electrons from positrons.

The $S$-matrix for the process in figure 7.3 is

$$S_{fi} = +ie\int d^4x \overline{\psi}_f(x)\not{\!\!A}(x)\Psi_i^{(-)}(x) .$$ (7.80)

Here the incoming state is in the future and is to be interpreted as a negative-energy electron of four-momentum $-p_f$ running backward in time. Putting in plane waves to lowest order, the wave function is

$$\psi_i(x) = \sqrt{\frac{m}{E_fV}} v(p_f,s_f) e^{+ip_f\cdot x} .$$ (7.81)

Similarly, the outgoing state is the negative-energy electron running backward into the past. Its wave function is

$$\psi_f(x) = \sqrt{\frac{m}{E_iV}} v(p_i,s_i) e^{+ip_i\cdot x}$$ (7.82)

representing the incident positron with momentum $\vec{p}_i$ and polarization $\vec{s}_i$ before the scattering. The $S$-matrix becomes (cf equation 7.30)

$$S_{fi} = -\frac{iZe^2}{4\pi} \frac{1}{V} \sqrt{\frac{m^2}{E_... ...f) \int \frac{d^4x}{\vert\vec{x}\vert} e^{i(p_f-p_i)\cdot x} .$$ (7.83)

By the same calculation as in equation 7.45, we find the differential cross-section is

$$\left( \frac{d\overline{\sigma}}{d\Omega} \right)_{e^+} = \f... ...f,s_i} \vert\overline{v}(p_i,s_i) \gamma^0 v(p_f,s_f)\vert^2 .$$ (7.84)

Again the spin sum may be reduced to a trace, using the relation for positron spinors

$$\sum_{\pm s_i} v_\alpha(p_i,s_i)\overline{v}_\beta(p_i,s_i) ... ...eft( \frac{-\not{\;\!\!\!p}_i + m}{2m} \right)_{\alpha\beta} .$$ (7.85)

The first minus sign comes from the normalization of the negative-energy spinors and the relative minus sign of the two terms comes from the negative-energy projection operator.

The differential cross-section now becomes

$$\left( \frac{d\overline{\sigma}}{d\Omega} \right)_{e^+} = \f... ...ot{\;\!\!\!p}_i - m) \gamma^0 (\not{\;\!\!\!p}_f - m)\right] .$$ (7.86)

This is the same as the result of equation 7.50 for the electron with $m$ replaced by $-m$. Since our answer for electron scattering was even in $m$, this shows that the positron scattering cross-section is equal to the electron scattering cross-section in lowest order of $\alpha$.

We could have anticipated this result from charge conjugation invariance. We could equally well write

$$S_{fi} = +ie\int d^4x \overline{\psi}_{ci}(x) \not{\!\!A}\psi_{cf}(x) ,$$

$$= -ie\int d^4x \psi_i^T(x) C^{-1} \not{\!\!A}C \overline{\psi}_f^T(x) ,$$

$$= +ie\int d^4x \psi_i^T(x) \not{\!\!A}^T \overline{\psi}_f^T(x) ,$$

$$= ie\int d^4x \overline{\psi}_f(x) \not{\!\!A}\psi_i(x) ,$$ (7.87)

which leads to the same results as before. In this picture the positron runs forward in time and $\psi_{cf}(x) = C \gamma^0 \psi_f^*$ is the wave function of the initial positron.

Previously we saw that for each solution of the electron in the potential $A_\mu$ there is a corresponding solution of the positron in the potential $-A_\mu$, that is, the scattering of an electron from the potential $-e/4\pi r$ is the same as that of a positron from potential $+e/4\pi r$; however, since the calculated cross-section depends only on $e^4$, the sign of $A_\mu$ does not matter. This is not true for the $e^6$ correction which comes from the product of the first- and second-order scattering amplitudes, which have opposite signs for electrons and positrons.

We may also observe that the positron cross-section is obtained from that of the electron by replacing $p_i\leftrightarrow -p_f$; this is a general feature of positron theory called the ``substitution rule'', which is closely related to the propagator picture we have developed.