Skip to main content

Section 5.6 Surface integrals

Step 4: we define integration of a two-form along a parametric surface via pullback. We call those “surface integrals”. Step 5: we show that the integral is well-defined: it is invariant under orientation-preserving reparametrizations, and changes sign under orientation-reversing reparametrizations. This ensures that the integral of the two-form is intrinsically defined in terms of the geometry of the image surface with its induced orientation. We also rewrite surface integrals in terms of vector fields.

Subsection 5.6.1 The definition of surface integrals

We define the integral of a two-form along a parametric surface: we pull back to the region \(D\) and integrate.

Definition 5.6.1. Surface integrals.

Let \(\omega\) be a two-form on an open subset \(U \subseteq \mathbb{R}^3\text{.}\) Let \(\alpha: D \to \mathbb{R}^3\) be a parametric surface whose image surface \(S = \alpha(D) \subset U\) is orientable. We define the surface integral of \(\omega\) along \(\alpha\) as:

\begin{equation*} \int_\alpha \omega = \int_D \alpha^* \omega, \end{equation*}

where the integral on the right-hand-side is defined in Definition 5.3.1, with \(D\) given the canonical orientation (which is consistent with the induced orientation on \(S\)).

What is neat is that by Definition 5.3.1, the integral on the right-hand-side can be written as a standard double integral from calculus. So using the pullback we reduced the evaluation of integrals of two-forms over surfaces to standard double integrals!

Consider the two-form \(\omega = x\ dy \wedge dz + z\ dx \wedge dy\text{.}\) Evaluate its surface integral along the oriented parametric surface \(\alpha: D \to \mathbb{R}^3\) with \(D = \{(u,v) \in \mathbb{R}^2~|~ u \in [0,1], v \in [0,2] \}\) and \(\alpha(u,v) = (u, u v^2, v) \text{.}\)

We calculate the pullback of the two-form:

\begin{align*} \alpha^* \omega =\amp u \left( v^2\ du + 2 u v\ dv \right) \wedge dv + v du \wedge \left( v^2\ du + 2 u v\ dv \right)\\ =\amp (u v^2 + 2 u v^2) du \wedge dv\\ =\amp 3 u v^2 du \wedge dv. \end{align*}

The surface integral then becomes:

\begin{align*} \int_\alpha \omega =\amp \int_D 3 u v^2\ du \wedge dv\\ =\amp 3 \int_0^2 \int_0^1 u v^2\ du dv\\ =\amp 3\int_0^2 v^2 \left[\frac{u^2}{2} \right]_0^1 dv \\ =\amp \frac{3}{2} \int_0^2 v^2\ dv\\ =\amp \frac{v^3}{2} \Big|_0^2\\ =\amp 4. \end{align*}

Note that it is important here that we wrote the two-form \(\alpha^* \omega\) in terms of the basic two-form \(du \wedge dv \) (not \(dv \wedge du\)) before rewriting as a double integral, as the orientation on \(D\) is the canonical orientation with respect to the coordinates \((u,v)\) on \(D \subset \mathbb{R}^2\text{.}\)

Subsection 5.6.2 Reparametrization-invariance and orientability of surface integrals

We defined surface integrals in terms of parametric surfaces: the parametrization was key, as we used it to pullback to \(D\text{.}\) But in the end, we would like our integral to be defined solely in terms of the image surface \(S\) itself with its orientation. If we use two different parametrizations that describe the same surface with the same induced orientation, we want the integral to be the same. The integral should not depend on how we describe the surface, as long as we preserve the induced orientation.

Let us rewrite the two surface integrals using the pullback. First,

\begin{equation*} \int_\alpha \omega = \int_{D_1} \alpha^* \omega. \end{equation*}

Second,

\begin{equation*} \int_{\phi^* \alpha} \omega = \int_{D_2} (\alpha \circ \phi)^* \omega. \end{equation*}

From Exercise 4.7.4.7, we know that we can pullback through a chain of maps \(D_2 \overset{\phi}{\rightarrow} D_1 \overset{\alpha}{\rightarrow} \mathbb{R}^3\) in two different ways, but it gives the same thing: \((\alpha \circ \phi)^* \omega = \phi^*(\alpha^* \omega) \text{.}\) Therefore,

\begin{equation*} \int_{\phi^* \alpha} \omega = \int_{D_2} \phi^* (\alpha^* \omega). \end{equation*}

In the end, what we need to compare is two integrals over regions in \(\mathbb{R}^2\text{.}\) But this is precisely the result of Lemma 5.3.7, for the two-form \(\alpha^* \omega\) on \(D_1\text{.}\) This lemma states that if \(\det J_\phi >0\text{,}\) then

\begin{equation*} \int_{D_1} \alpha^* \omega = \int_{D_2} \phi^* (\alpha^* \omega), \end{equation*}

while if \(\det J_\phi \lt 0\text{,}\)

\begin{equation*} \int_{D_1} \alpha^* \omega =- \int_{D_2} \phi^* (\alpha^* \omega), \end{equation*}

We thus conclude that if the reparametrization is orientation-preserving,

\begin{equation*} \int_\alpha \omega = \int_{\phi^* \alpha} \omega, \end{equation*}

while if it is orientation-reversing,

\begin{equation*} \int_\alpha \omega = -\int_{\phi^* \alpha} \omega. \end{equation*}

Surface integrals are oriented and reparametrization-invariant, as we want. Nice! As a result, while we use a parametrization to define a surface integral, the integral can really be thought of as being defined intrinsically in terms of the surface \(S\) and its orientation.

Subsection 5.6.3 Surface integrals in terms of vector fields

Let us now translate our definition in surface integrals in terms of vector fields, using the dictionary between differential forms and vector calculus concepts that we established.

We first need to do a bit of work to rephrase the pullback of a two-form along a parametric surface in terms of associated vector fields.

This is just a calculation:

\begin{align*} \alpha^* \omega =\amp f(\alpha(u,v)) \left(\frac{\partial y}{\partial u}\ du + \frac{\partial y}{\partial v}\ dv \right) \wedge \left(\frac{\partial z}{\partial u}\ du + \frac{\partial z}{\partial v}\ dv \right) \\ \amp+ g(\alpha(u,v) ) \left(\frac{\partial z}{\partial u}\ du + \frac{\partial z}{\partial v}\ dv \right) \wedge \left(\frac{\partial x}{\partial u}\ du + \frac{\partial x}{\partial v}\ dv \right) \\ \amp+ h(\alpha(u,v) ) \left(\frac{\partial x}{\partial u}\ du + \frac{\partial x}{\partial v}\ dv \right) \wedge \left(\frac{\partial y}{\partial u}\ du + \frac{\partial y}{\partial v}\ dv \right) \\ =\amp f(\alpha(u,v)) \left( \frac{\partial y}{\partial u}\frac{\partial z}{\partial v} - \frac{\partial y}{\partial v}\frac{\partial z}{\partial u} \right) du \wedge dv\\ \amp+g(\alpha(u,v)) \left( \frac{\partial z}{\partial u}\frac{\partial x}{\partial v} - \frac{\partial z}{\partial v}\frac{\partial x}{\partial u} \right) du \wedge dv\\ \amp+h(\alpha(u,v)) \left( \frac{\partial x}{\partial u}\frac{\partial y}{\partial v} - \frac{\partial x}{\partial v}\frac{\partial y}{\partial u} \right) du \wedge dv\\ =\amp \mathbf{F}(\alpha(u,v) ) \cdot \left( \mathbf{T}_u \times \mathbf{T}_v \right) du \wedge dv. \end{align*}

It is interesting to remark here that while pulling back a one-form along a parametric curve picked the tangential component of the vector field along the curve, pulling back a two-form along a parametric surface picks the normal component of the vector field. This has an interpretation in physics, as we will see. Just as line integrals were related to the calculation of work (and hence the tangential component of the force field to the direction of motion was the relevant one), surface integrals are related to the calculation of flux, for which the normal component of the force field is the relevant one.

With this result, we can rewrite surface integrals directly as double integrals:

This follows directly from Lemma 5.6.4, the definition of surface integrals Definition 5.6.1, and the definition of integrals over region in \(\mathbb{R}^2\) Definition 5.3.1. We have:

\begin{align*} \int_\alpha \omega =\amp \int_D \alpha^* \omega\\ =\amp \int_D \left( \mathbf{F}(\alpha(u,v)) \cdot \mathbf{n} \right) du \wedge dv\\ =\amp \iint_D \left( \mathbf{F}(\alpha(u,v)) \cdot \mathbf{n}\right) dA. \end{align*}

This is how surface integrals are generally defined in standard vector calculus textbooks.

Remark 5.6.6.

Sometimes, the following shorthand notation is used:

\begin{equation*} \iint_S \mathbf{F} \cdot d \mathbf{S} := \iint_D \left( \mathbf{F}(\alpha(u,v)) \cdot \mathbf{n}\right) dA. \end{equation*}

Such integrals are also called flux integrals, because of the physics interpretation, which we will study in Section 5.9. The integral calculates the flux of the vector field \(\mathbf{F}\) across the surface \(S\) in the direction of the normal vector \(\mathbf{n}\) specified by the orientation.

Calculate the surface integral of the vector field

\begin{equation*} \mathbf{F} = \frac{1}{x^2+y^2+z^2} \left( x, y, 0 \right) \end{equation*}

over the upper half-sphere of radius one, with the inwards orientation.

We can use our parametrization from Example 5.5.6 with \(R=1\text{,}\) that is, \(\alpha: D \to \mathbb{R}^3\text{,}\) with

\begin{equation*} D = \{(\theta,\phi) \in \mathbb{R}^2~|~ \theta \in \left[ 0,\frac{\pi}{2} \right], \phi \in [0,2 \pi] \}, \end{equation*}

and

\begin{equation*} \alpha(\theta,\phi) = ( \sin(\theta) \cos(\phi), \sin(\theta) \sin(\phi), \cos(\theta) ). \end{equation*}

We showed in that example that the normal vector points outwards, so the orientation on the upper half-sphere induced by this parametrization is opposite to what is asked in the problem. Therefore, we will need to take minus the integral over the parametric surface \(\alpha\text{.}\)

We calculated in Example 5.5.6 the normal vector:

\begin{equation*} \mathbf{n} = \left( \sin^2(\theta) \cos(\phi), \sin^2(\theta) \sin(\phi), \sin(\theta)\cos(\theta) \right). \end{equation*}

The integrand is then (noting that \(x^2+y^2+z^2=1\) on the surface):

\begin{align*} \mathbf{F}(\alpha(\theta,\phi) ) \cdot \mathbf{n} =\amp \left( \sin(\theta) \cos(\phi), \sin(\theta) \sin(\phi), 0 \right) \cdot \left( \sin^2(\theta) \cos(\phi), \sin^2(\theta) \sin(\phi), \sin(\theta)\cos(\theta) \right)\\ =\amp \sin^3(\theta) \cos^2(\phi) + \sin^3(\theta) \sin^2(\phi) \\ =\amp \sin^3(\theta). \end{align*}

The surface integral then becomes (recall that we need to add a minus sign since the surface integral is with respect to the inwards orientation, while our parametrization induces the outwards orientation):

\begin{align*} \iint_S \mathbf{F} \cdot d \mathbf{S} =\amp -\int_0^{2 \pi} \int_0^{\frac{\pi}{2}} \sin^3(\theta) d \theta d \phi \\ =\amp- \int_0^{2 \pi} \left[ - \cos(\theta)+\frac{1}{3} \cos^3(\theta) \right]_0^{\frac{\pi}{2}} d \phi\\ =\amp - \frac{2}{3} \int_0^{2 \pi} d \phi\\ =\amp- \frac{4 \pi}{3}. \end{align*}

Exercises 5.6.4 Exercises

1.

Find the surface integral of the two-form

\begin{equation*} \omega = y\ dy \wedge dz - (x+y)\ dz \wedge dx \end{equation*}

along the lower half-sphere \(x^2+y^2+z^2 = 4\text{,}\) \(z \leq 0\text{,}\) with orientation given by an inwards pointing normal vector.

Solution.

We use spherical coordinates to parametrize the lower half sphere of radius \(2\text{.}\) That is, \(\alpha:D \to \mathbb{R}^3\) with

\begin{equation*} D = \{(\theta,\phi) \in \mathbb{R}^2\ | \ \theta \in \left[ \frac{\pi}{2},\pi \right], \phi \in [0, 2 \pi] \}, \end{equation*}

and

\begin{equation*} \alpha(\theta,\phi) = (2 \sin(\theta) \cos(\phi), 2 \sin(\theta) \sin(\phi), 2 \cos(\theta) ). \end{equation*}

Here the inclination angle was restricted to be between \(\pi/2\) and \(\pi\text{,}\) which amounts to considering the lower half-sphere with \(z \leq 0\text{.}\) We have already calculated in Example 5.5.6 the this parametrization induces a normal vector pointing outwards. The question is asking us to pick the opposite orientation, with normal vector pointing inwards. So we will have to add an overall minus sign to our surface integral.

To evaluate the surface integral we first need to calculate the pullback \(\alpha^* \omega\text{.}\) We get:

\begin{align*} \alpha^* \omega =\amp 2 \sin(\theta) \sin(\phi) (2 \cos(\theta) \sin(\phi) d\theta + 2 \sin(\theta) \cos(\phi)d \phi) ) \wedge (- 2 \sin(\theta) d\theta)\\ \amp - (2 \sin(\theta) \cos(\phi)+2 \sin(\theta)\sin(\phi) ) (- 2 \sin(\theta) d \theta) \wedge (2 \cos(\theta) \cos(\phi) d\theta - 2 \sin(\theta) \sin(\phi) d\phi) \\ =\amp - 8 \sin^3(\theta) \sin(\phi) \cos(\phi) d \phi \wedge d \theta - 8 \sin^3(\theta) \sin(\phi) (\cos(\phi)+\sin(\phi) ) d \theta \wedge d \phi \\ =\amp - 8 \sin^3(\theta) \sin^2(\phi) d \theta \wedge d \phi. \end{align*}

Then we integrate, recalling that we have to add a minus sign because of the orientation:

\begin{align*} - \int_\alpha \omega =\amp - \int_D \alpha^* \omega \\ =\amp 8 \int_{\pi/2}^{\pi} \int_0^{2 \pi} \sin^3(\theta) \sin^2(\phi) d \phi d \theta\\ =\amp 8 \pi \int_{\pi/2}^{\pi} \sin^3(\theta) d \theta\\ =\amp \frac{16 \pi}{3}, \end{align*}

where I used the fact that

\begin{equation*} \int_0^{2 \pi} \sin^2(\phi)d\phi = \pi, \qquad \int_{\pi/2}^{\pi} \sin^3(\theta) d\theta = \frac{2}{3}, \end{equation*}

which you can check independently using trigonometric identities to evaluate the definite integrals.

2.

Find the flux (the surface integral) of the vector field

\begin{equation*} \mathbf{F}(x,y,z) = (z e^{ xy}, - 3z e^{x y} , 2 x y) \end{equation*}

along the parallelogram realized as the parametric surface \(\alpha: D \to \mathbb{R}^3\) with \(D = \{(u,v) \in \mathbb{R}^2\ | \ u \in [0,2], v\in [0,1] \} \) and

\begin{equation*} \alpha(u,v) = (u+v, u-v, 1+2u + v). \end{equation*}
Solution.

Let us solve this problem using the vector field approach. We know the parametric surface; we need to calculate the normal vector. The tangent vectors are

\begin{equation*} \mathbf{T}_u = (1,1,2), \qquad \mathbf{T}_v = (1,-1,1). \end{equation*}

(We note that those are constant vectors, since the image surface is planar.) The normal vector is then

\begin{align*} \mathbf{n} =\amp \mathbf{T}_u \times \mathbf{T}_v\\ =\amp \det \begin{pmatrix} \mathbf{i} \amp \mathbf{j} \amp \mathbf{k} \\ 1 \amp 1 \amp 2 \\ 1 \amp -1 \amp 1 \end{pmatrix}\\ =\amp ( 3, 1, -2 ). \end{align*}

We then calculate the surface integral:

\begin{align*} \iint_D \mathbf{F} \cdot d \mathbf{S} =\amp \int_0^2 \int_0^1 ( (1+2u+v) e^{ u^2-v^2}, - 3(1+2u+v) e^{u^2-v^2}, 2(u^2-v^2)) \cdot (3,1,-2)\ dv du\\ =\amp \int_0^2 \int_0^1 \left( -4(u^2-v^2) \right)\ dv du\\ =\amp -4 \int_0^2 \left[ u^2 v - \frac{v^3}{3} \right]_{v=0}^{v=1} \ du\\ =\amp -4 \int_0^2 \left( u^2 - \frac{1}{3} \right)\ du \\ =\amp -4 \left[ \frac{u^3}{3} - \frac{u}{3} \right]_{u=0}^{u=2} \\ =\amp - 8. \end{align*}

3.

Find the surface integral of the two-form

\begin{equation*} \omega = x \ dy \wedge dz + z\ dx \wedge dy \end{equation*}

over the surface of the cube with vertices \((\pm 1, \pm 1, \pm 1)\text{,}\) with orientation given by a normal vector pointing outwards.

Solution.

The cube is shown in the figure below. It has six sides, which we consider as separate parametric surfaces, \(S_i\) with \(i=1,\ldots,6\text{.}\)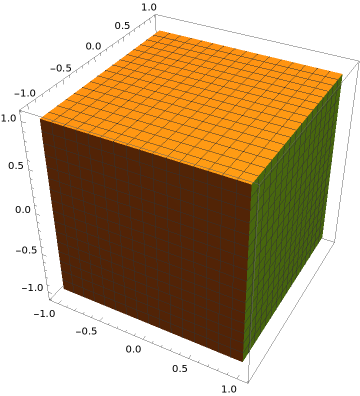

The surface.
Figure 5.6.8. The surface \(S\) is the cube shown in the figure. We consider the six sides as separate parametric surfaces.

All six sides can be parametrized easily, with the same domain \(D\text{.}\) We write the parametrizations as \(\alpha_i: D \to \mathbb{R}^3\text{,}\) for \(i=1,\ldots,6\text{,}\) with

\begin{equation*} D = \{(u,v) \in \mathbb{R}^2\ |\ u \in [-1, 1], v\in [-1,1] \}, \end{equation*}

and

\begin{align*} \alpha_1(u,v) =\amp (1, u, v)\\ \alpha_2(u,v) =\amp (-1, u, v)\\ \alpha_3(u,v) =\amp ( u,1, v)\\ \alpha_4(u,v) =\amp (u,-1, v)\\ \alpha_5(u,v) =\amp (u, v,1)\\ \alpha_6(u,v) =\amp (u, v,-1) \end{align*}

Calculating the normal vectors, we see that the normal vectors for \(\alpha_1, \alpha_4, \alpha_5\) point outwards, while the normal vectors for \(\alpha_2, \alpha_3, \alpha_6\) point inwards. So we can write our desired surface integral as

\begin{equation*} \int_S \omega = \int_{S_1} \omega- \int_{S_2} \omega-\int_{S_3} \omega+\int_{S_4} \omega+\int_{S_5} \omega-\int_{S_6} \omega. \end{equation*}

To calculate these surface integrals, we need the pullbacks. A straightforward calculation gives:

\begin{gather*} \alpha_1^* \omega = \alpha_5^* \omega = du \wedge dv,\\ \alpha_2^* \omega = \alpha_6^* \omega = - du \wedge dv,\\ \alpha_3^* \omega = \alpha_4^* \omega = 0. \end{gather*}

Therefore,

\begin{align*} \int_S \omega =\amp \int_{S_1} \omega- \int_{S_2} \omega-\int_{S_3} \omega+\int_{S_4} \omega+\int_{S_5} \omega-\int_{S_6} \omega\\ =\amp 4 \int_D du \wedge dv\\ =\amp 4 \int_{-1}^1 \int_{-1}^1 du dv\\ =\amp 16. \end{align*}

4.

Let \(S\) be the boundary of the region in \(\mathbb{R}^3\) enclosed by the cylinder \(x^2 + y^2 = 4\text{,}\) the paraboloid \(z = x^2+y^2\text{,}\) and the plane \(z=9\text{.}\) Find the surface integral of the vector field

\begin{equation*} \mathbf{F}(x,y,z) = (x^2, y^2, z^2) \end{equation*}

along \(S\) with orientation given by a normal vector pointing inwards.

Solution.

We see that the cylinder \(x^2+y^2=4\) and the paraboloid \(z=x^2+y^2\) intersect along the circle \(x^2+y^2=4\) in the plane \(z=4\text{.}\) Thus the surface \(S\) has three components: \(S_1\) is the part the paraboloid \(z = x^2+y^2\) with \(0 \leq z \leq 4\text{;}\) \(S_2\) is the part of the cylinder \(x^2+y^2 = 4\) with \(4 \leq z \leq 9\text{;}\) and \(S_3\) is the disk \(x^2+y^2 \leq 4\) in the plane \(z=9\text{.}\) This is shown in Figure 5.6.9.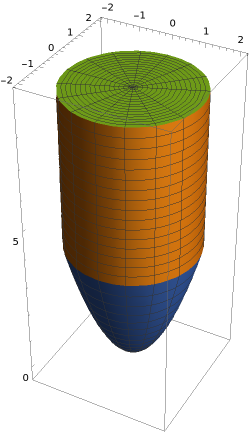

The surface.
Figure 5.6.9. The surface \(S\) has three components: \(S_1\) is the part of the paraboloid (in blue) with \(z \leq 4\text{;}\) \(S_2\) is the lateral surface of the cylinder (in orange) for \(4 \leq z \leq 9\text{;}\) \(S_3\) is the disk \(x^2+y^2 \leq 4\) in the plane \(z=9\) (in green).

To evaluate the surface integral of \(\omega\) over \(S\text{,}\) we evaluate it over the three components separately and then add up the integrals.

Let us consider \(S_1\) first, which is the part of the paraboloid \(z = x^2+y^2\) with \(0 \leq z \leq 4\text{.}\) We realize it as the parametric surface \(\alpha_1: D_1 \to \mathbb{R}^3\) with

\begin{equation*} D_1 = \{(u, \theta) \in \mathbb{R}^2\ |\ u \in [0, 2], \theta \in [0, 2 \pi] \} \end{equation*}

and

\begin{equation*} \alpha_1(u,\theta) = (u \cos(\theta), u \sin(\theta), u^2 ). \end{equation*}

We need to make sure that the normal vector points inwards. The tangent vectors are

\begin{equation*} \mathbf{T}_u = (\cos(\theta), \sin(\theta), 2 u), \qquad \mathbf{T}_\theta = (-u \sin(\theta), u \cos(\theta), 0). \end{equation*}

The normal vector is

\begin{equation*} \mathbf{n} = \mathbf{T}_u \times \mathbf{T}_\theta = ( - 2 u^2 \cos(\theta), - 2 u^2 \sin(\theta), u). \end{equation*}

As \(u \geq 0\text{,}\) we see that the normal vector points in the positive \(z\)-direction, which means that it points inwards. So we're good!

We then evaluate the surface integral:

\begin{align*} \iint_{S_1} \mathbf{F} \cdot d \mathbf{S}_1 =\amp \int_0^2 \int_0^{2 \pi} \left( (u^2 \cos^2(\theta), u^2 \sin^2(\theta), u^4) \cdot (- 2 u^2 \cos(\theta), - 2 u^2 \sin(\theta), u) \right)\ d\theta du\\ =\amp \int_0^2 \int_0^{2 \pi} \left( - 2 u^4 (\cos^3(\theta) + \sin^3(\theta) ) + u^5 \right) d\theta du\\ =\amp 2 \pi \int_0^2 u^5\ du\\ =\amp \frac{64 \pi}{3}, \end{align*}

where we used the fact that \(\int_0^{2 \pi} \cos^3(\theta) d \theta = \int_0^{2 \pi} \sin^3(\theta) d\theta =0\text{.}\)

Let us now consider \(S_2\text{,}\) which is the cylinder \(x^2+y^2=4\text{,}\) \(4 \leq z \leq 9\text{.}\) We parametrize it as \(\alpha_2: D_2 \to \mathbb{R}^3\) with

\begin{equation*} D_2 = \{(u, \theta) \in \mathbb{R}^2\ |\ u \in [4, 9], \theta \in [0, 2 \pi ] \} \end{equation*}

and

\begin{equation*} \alpha_2(u,\theta) = (2 \cos(\theta), 2 \sin(\theta), u). \end{equation*}

We look at the normal vector. The tangent vectors are

\begin{equation*} \mathbf{T}_u = (0,0,1), \qquad \mathbf{T}_\theta = (-2 \sin(\theta), 2 \cos(\theta), 0), \end{equation*}

and the normal vector is

\begin{equation*} \mathbf{n} = \mathbf{T}_u \times \mathbf{T}_\theta = (- 2 \cos(\theta), - 2 \sin(\theta), 0 ). \end{equation*}

We thus see that at a point with coordinates \((2 \cos(\theta), 2 \sin(\theta), u) \) on the cylinder, the normal vector is \((-2 \cos(\theta), -2 \sin(\theta), 0)\text{,}\) which points inwards. Good!

We evaluate the surface integral:

\begin{align*} \iint_{S_2} \mathbf{F} \cdot d \mathbf{S}_2 =\amp \int_4^9 \int_0^{2 \pi} \left( (4 \cos^2(\theta), 4 \sin^2(\theta), u^2) \cdot (- 2 \cos(\theta), - 2 \sin(\theta), 0 ) \right) d\theta du\\ =\amp \int_4^9 \int_0^{2 \pi} \left( - 8 \cos^3(\theta) - 8 \sin^3(\theta) \right) d \theta du\\ =\amp 0, \end{align*}

since, as above, \(\int_0^{2 \pi} \cos^3(\theta) d \theta = \int_0^{2 \pi} \sin^3(\theta) d\theta =0\text{.}\)

Finally, we consider \(S_3\text{,}\) which is the disk \(x^2+y^2 \leq 4\) in the plane \(z=9\text{.}\) We parametrize it as \(\alpha_3: D_3 \to \mathbb{R}^3\) with

\begin{equation*} D_3 = \{(u, \theta) \in \mathbb{R}^2\ |\ u \in [0,2], \theta \in [0, 2 \pi ] \} \end{equation*}

and

\begin{equation*} \alpha_3(u,\theta) = (u \sin(\theta), u \cos(\theta), 9). \end{equation*}

The tangent vectors are

\begin{equation*} \mathbf{T}_u = (\sin(\theta), \cos(\theta), 0), \qquad \mathbf{T}_\theta = ( u \cos(\theta), -u \sin(\theta), 0), \end{equation*}

and the normal vector is

\begin{equation*} \mathbf{n} = \mathbf{T}_u \times \mathbf{T}_\theta = (0,0,-u). \end{equation*}

As \(u \geq 0\text{,}\) this points in the negative \(z\)-direction, that is, it points inwards, as we want.

We evaluate the surface integral:

\begin{align*} \iint_{S_3} \mathbf{F} \cdot d \mathbf{S}_3 =\amp \int_0^2 \int_0^{2 \pi} \left( (u^2 \sin^2(\theta), u^2 \cos^2(\theta), 81) \cdot (0, 0, -u ) \right) d\theta du\\ =\amp \int_0^2 \int_0^{2 \pi} (-81 u) d\theta du\\ =\amp -162 \pi \int_0^2 u du,\\ =\amp - 324 \pi. \end{align*}

Finally, we compute the surface integral over \(S\) by adding up the three surface integrals aboves. We get:

\begin{align*} \iint_S \mathbf{F} \cdot d \mathbf{S} =\amp \iint_{S_1} \mathbf{F} \cdot d \mathbf{S}_1 +\iint_{S_2} \mathbf{F} \cdot d \mathbf{S}_2 +\iint_{S_3} \mathbf{F} \cdot d \mathbf{S}_3\\ =\amp \frac{64 \pi}{3} + 0 - 324 \pi\\ =\amp - \frac{908 \pi}{3}. \end{align*}

Done! :-)

5.

An “inverse square field” is a vector field \(\mathbf{F}\) that is inversely proportional to the square of the distance from the origin. It is very important in physics, as it describes many physical phenomena, such a gravity, electrostatics, etc. It can be written as

\begin{equation*} \mathbf{F}(x,y,z) = C \frac{1}{(x^2+y^2+z^2)^{3/2}} (x,y,z), \end{equation*}

for some constant \(C \in \mathbb{R}\text{.}\) Show that the flux (the surface integral) of \(\mathbf{F}\) across a sphere \(S\) centered at the origin (in the outwards direction) is independent of the radius of \(S\text{.}\) This is one of the very nice properties of inverse square fields!

Solution.

As usual we use spherical coordinates to parametrize the sphere of fixed radius \(R\text{,}\) as \(\alpha:D \to \mathbb{R}^3\text{,}\) with

\begin{equation*} D = \{(\theta,\phi) \in \mathbb{R}^2\ | \ \theta \in \left[ 0,\pi \right], \phi \in [0, 2 \pi] \}, \end{equation*}

and

\begin{equation*} \alpha(\theta,\phi) = (R \sin(\theta) \cos(\phi), R \sin(\theta) \sin(\phi), R \cos(\theta) ). \end{equation*}

Let use differential forms to calculate the surface integral. To the vector field \(\mathbf{F}\) we associated the two-form

\begin{equation*} \omega = C \frac{1}{(x^2+y^2+z^2)^{3/2}} \left( x\ dy \wedge dz+ y\ dz \wedge dx+ z\ dx \wedge dy \right). \end{equation*}

To calculate the surface integral, we calculate the pullback, noting that \(x(\theta,\phi)^2+y(\theta,\phi)^2+z(\theta,\phi)^2 = R^2\) :

\begin{align*} \alpha^* \omega =\amp \frac{C}{R^3} ( R \sin(\theta) \cos(\phi) (R \cos(\theta) \sin(\phi) d\theta + R \sin(\theta)\cos(\phi)d\phi) \wedge (-R \sin(\theta) d\theta) \\ \amp + R \sin(\theta)\sin(\phi) (- R \sin(\theta) d\theta )\wedge (R \cos(\theta) \cos(\phi) d\theta - R \sin(\theta) \sin(\phi) d\phi) \\ \amp + R \cos(\theta) (R \cos(\theta) \cos(\phi) d\theta) - R \sin(\theta) \sin(\phi) d\phi) \wedge (R \cos(\theta) \sin(\phi) d\theta + R \sin(\theta)\cos(\phi)d\phi) )\\ =\amp \frac{C R^3}{R^3} (\sin^3(\theta)\cos^2(\phi) + \sin^3(\theta) \sin^2(\phi) +\cos^2(\theta) \sin(\theta) \cos^2(\phi) + \cos^2(\theta)\sin(\theta) \sin^2(\phi) ) d \theta \wedge d \phi\\ =\amp C \sin(\theta) d \theta \wedge d \phi. \end{align*}

In particular, we see that it does not depend on the radius \(R\) of the sphere! The surface integral is then

\begin{align*} \int_\alpha \omega =\amp \int_D \alpha^* \omega \\ =\amp C \int_0^{2 \pi} \int_0^\pi \sin(\theta) d\theta d \phi\\ =\amp 2 C \int_0^{2 \pi} d\phi\\ =\amp 4 \pi C, \end{align*}

which is indeed independent of the radius \(R\text{.}\)