Stokes' theorem

Section 5.8 Stokes' theorem

Step 6, part 2: we continue our study of integration of exact two-forms. But this time we consider surface integrals, that is integrals of exact two-forms over parametric surfaces. The result is Stokes' theorem.

🔗

Objectives

You should be able to:

State Stokes' theorem for integrals of exact two-forms over parametric surfaces in $R^{3} .$
Rephrase Stokes' theorem in terms of the associated vector fields.
Show that Stokes' theorem implies that the integral of an exact two-form over a closed surface in $R^{3}$ vanishes.
Use Stokes' theorem to evaluate surface integrals of exact two-forms.
Use Stokes' theorem to evaluate line integrals of one-forms over closed curves in $R^{3} .$
Use Stokes' theorem and its consequences to show that a given two-form cannot be exact.

🔗

Subsection 5.8.1 Stoke's theorem

🔗

In the previous section we studied integrals of exact two-forms over bounded regions in

R^{2} .

We now look at surface integrals of exact two-forms over parametric surfaces in

R^{3} .

🔗

As in the previous section, we start by recalling the corresponding statement for curves, which we first studied in Theorem 3.4.1, and revisited in Theorem 5.1.8. Without getting into the details again, the key statement is that the integral of an exact one-form

ω = d f

over a parametric curve

α

satisfies the property

\int_{α} d f = \int_{\partial α} f,

🔗

which is the Fundamental Theorem of line integrals rewritten using integrals of zero-forms. The integral on the left-hand-side is a line integral along the oriented parametric curve

α,

while on the right-hand-side we have the integral of the zero-form

f

over the oriented boundary

\partial α

of the parametric curve

α .

🔗

Looking back at Theorem 3.4.1, the proof of the Fundamental Theorem of line integrals basically amounted to pulling back to the interval

[a, b]

using the definition of line integrals, and then using the Fundamental Theorem of Calculus. We now do the same thing for surface integrals: we pull back to the region

D

and then use Green's theorem. The result is known as Stokes' theorem.

🔗

Theorem 5.8.1. Stokes' theorem.

Let $η$ be a one-form on an open subset $U \subseteq R^{3},$ and $α : D \to R^{3}$ a parametric surface whose image $S = α (D) \subset U$ is orientable and oriented by the parametrization. Let $\partial α$ be the boundary of the surface $S$ with its induced orientation, as in Definition 5.5.5 (if the image surface is closed, $\partial α$ is the empty set). Then the integral of the exact two-form $d η$ along the parametric surface $α$ can be evaluated as:

\int_{α} d η = \int_{\partial α} η .

In other words, the surface integral of the exact two-form $ω = d η$ along the parametric surface $α$ is equal to the line integral of the one-form $η$ along its oriented boundary curve.

🔗

Proof.

Stokes' theorem pretty much follows from Green's theorem by pullback. More precisely, by definition of the surface integral,

\int_{α} d η = \int_{D} α^{*} (d η) .

We know that the exterior derivative commutes with pullback, see Lemma 4.7.4: $α^{*} (d η) = d (α^{*} η) .$ So we can rewrite the surface integral as:

\int_{α} d η = \int_{D} d (α^{*} η) .

This is now the integral of the exact two-form $d (α^{*} η)$ over a closed bounded region $D .$ By Green's theorem, Theorem 5.7.1, we know that

\int_{D} d (α^{*} η) = \int_{\partial D} α^{*} η,

where on the right-hand-side we have a line integral of the one-form $α^{*} η$ along the boundary of the closed region $D \subset R^{2} .$

We are almost done, but not quite: the last step is actually quite subtle. We would like to say that

\int_{\partial D} α^{*} η \overset{?}{=} \int_{\partial α} η .

If the parametrization $α$ is injective everywhere, then it maps the boundary $\partial D$ one-to-one to the boundary $\partial S,$ and so this equality follows from the definition of line integrals, thinking of $α$ restricted to the boundary $\partial D$ as a parametric curve (or a union of parametric curves). However, in general, it is a little more subtle; as we remarked in Remark 5.4.3, $\partial S \subseteq α (\partial D),$ but the two are not necessarily equal.¹ The general proof is beyond the scope of these notes. In any case, the conclusion would be that

\int_{α} d η = \int_{\partial α} η,

which is the statement of Stokes' theorem.

In fact, not only can

α

send boundary points in

\partial D

to points not on the boundary of

S,

but it can also map whole curves in

\partial D

to points in

S,

as it does for instance when parametrizing a sphere with spherical coordinates (two of the boundary lines of the rectangular regions are mapped to the north and south poles of the sphere).

🔗

Just as for the Fundamental Theorem of line integrals, there are two direct consequences of Stokes' theorem. First, the integrals of an exact two-form over two surfaces

S_{1}

and

S_{2}

that share the same oriented boundary are equal (this statement for surface integrals is analogous to path independence for line integrals of exact one-forms). Second, the integral of an exact two-form along a closed surface is zero (this statement for surface integrals is analogous to the statement that the line integral of an exact one-form along a closed curve vanishes). We state those as the following corollaries.

🔗

Corollary 5.8.2. The surface integrals of an exact two-form along two surfaces that share the same oriented boundary are equal.

Let $η$ be a one-form on $U \subseteq R^{3} .$ If $α : D_{1} \to R^{3}$ and $β : D_{2} \to R^{3}$ are two parametric surfaces whose image surfaces $S_{1} = α (D_{1}) \subset U$ and $S_{2} = β (D_{2}) \subset U$ share the same boundary $\partial S_{1} = \partial S_{2},$ with the same induced orientation, then

\int_{α} d η = \int_{β} d η .

🔗

Corollary 5.8.3. The surface integral of an exact two-form along a closed surface vanishes.

Let $η$ be a one-form on $U \subseteq R^{3} .$ If $α : D \to R^{3}$ is a parametric surface whose image surface $S = α (D) \subset U$ is closed (that is, it has no boundary, which means that it is itself the boundary of a volume), then

\int_{α} d η = 0.

🔗

Remark 5.8.4.

We can read Stokes' theorem in two ways, just like Green's theorem.

The integral of an exact two-form $ω = d η$ over the parametric surface $α : D \to R^{3}$ is equal to the line integral of the one-form $η$ over the oriented boundary $\partial α$ of the parametric surface.
The integral of a one-form $η$ over a closed oriented simple curve $\partial S$ in $R^{3}$ is equal to the surface integral of its exterior derivative $d η$ over any surface $S \subset R^{3}$ whose boundary is $\partial S,$ with the appropriate orientation.

These two different readings highlight the two different types of applications of Stokes' theorem: either to calculate surface integrals via the first reading, or to calculate line integrals via the second reading. We note that Corollary 5.8.2 can also be useful computationally, to replace a complicated surface integral by an easier one.

🔗

Example 5.8.5. Using Stokes' theorem to evaluate a surface integral by transforming it into a line integral.

Use Stokes' theorem to evaluate the surface integral of the two-form $ω = 2 z d y \land d z + d x \land d y$ along the part of the sphere $x^{2} + y^{2} + z^{2} = 25$ that is above the plane $z = 3,$ with orientation given by an outwards pointing normal vector.

The surface is shown in the following figure: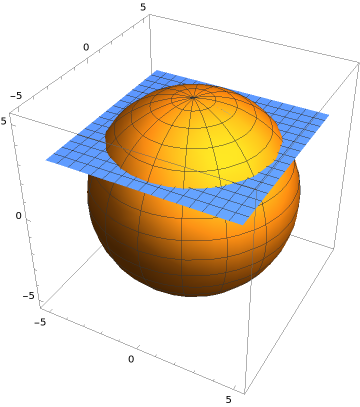

To start with, for Stokes' theorem to apply, the two-form $ω = 2 z d y \land d z + d x \land d y$ must be exact. But it easy to see that

η = (x - z^{2}) d y \Rightarrow d η = ω,

and thus $ω$ is exact.

The boundary $\partial S$ of the surface is the intersection of the sphere $x^{2} + y^{2} + z^{2} = 25$ and the plane $z = 3 .$ Setting $z = 3$ in the equation of the sphere, we get the equation of the circle $x^{2} + y^{2} = 25 - 9 = 16 .$ The boundary is thus the circle $x^{2} + y^{2} = 16$ in the plane $z = 3 .$ Since we orient the sphere with an outwards pointing normal vector, we see that must walk counterclockwise along the circle, with our heads pointing outside the sphere, to keep the region on our left. Therefore, the oriented boundary is the circle $x^{2} + y^{2} = 16$ in the plane $z = 3$ with counterclockwise orientation. Stokes' theorem then tells us that

\int_{S} d η = \int_{\partial S} η .

To evaluate the line integral on the right-hand-side we parametrize the oriented boundary with $α : [0, 2 π] \to R^{3},$

α (θ) = (4 \cos (θ), 4 \sin (θ), 3) .

We calculate the pullback of the one-form $η :$

\begin{aligned} α^{*} η = & (4 \cos (θ) - 9) (4 \cos (θ)) d θ \\ = & 4 (4 \cos^{2} (θ) - 9 \cos (θ)) d θ . \end{aligned}

The line integral is then:

\begin{aligned} \int_{α} η = & \int_{[0, 2 π]} α^{*} η \\ = & 4 \int_{0}^{2 π} (4 \cos^{2} (θ) - 9 \cos (θ)) d θ \\ = & 16 π, \end{aligned}

where we used the fact that $\int_{0}^{2 π} \cos (θ) = 0$ and $\int_{0}^{2 π} \cos^{2} (θ) = π .$

Therefore, by Stokes' theorem, we conclude that

\int_{S} d η = 16 π .

🔗

Example 5.8.7. Using Stokes' theorem to evaluate a surface integral by using a simpler surface.

Let us consider the same integral as in the previous example, Example 5.8.5. That is, we want to evaluate the surface integral of the two-form $ω = 2 z d y \land d z + d x \land d y$ along the part of the sphere $x^{2} + y^{2} + z^{2} = 25$ that is above the plane $z = 3,$ with orientation given by an outwards pointing normal vector.

We can use Stokes' theorem in a different way to evaluate this surface integral. Since we know that the two-form is exact (as $ω = d η$ with $η = (x - z^{2}) d u$ ), we know that its surface integral along any two surfaces $S$ and $S^{'}$ that share the same oriented boundary are equal. So instead of integrating over the part of the sphere above the $z = 3$ plane, we could replace this surface by a simpler surface that shares the same boundary, which in this case is the circle $x^{2} + y^{2} = 16$ in the plane $z = 3,$ as we saw in Example 5.8.5. In particular, we could take the surface $S^{'}$ to be the disk $x^{2} + y^{2} \leq 16$ in the plane $z = 3,$ with orientation given by a normal vector pointing upwards. By Stokes' theorem, we know that

\int_{S} ω = \int_{S^{'}} ω,

so we can evaluate the surface integral over the oriented disk instead.

To do so, we parametrize the disk by $α : D \to R^{3},$ with

D = {(r, θ) \in R^{2} | r \in [0, 4], θ \in [0, 2 π]}

and

α (r, θ) = (r \cos (θ), r \sin (θ), 3) .

It is easy to see that the normal vector $n = T_{r} \times T_{θ}$ points upwards, as required. We calculate the pullback two-form:

\begin{aligned} α^{*} ω = & 2 (3) (\sin (θ) d r + r \cos (θ) d θ) \land (0) + (\cos (θ) d r - r \sin (θ) d θ) \land (\sin (θ) d r + r \cos (θ) d θ) \\ = & r d r \land d θ . \end{aligned}

The surface integral is then:

\begin{aligned} \int_{α} ω = & \int_{D} α^{*} ω \\ = & \int_{0}^{2 π} \int_{0}^{4} r d r d θ \\ = & \int_{0}^{2 π} {[\frac{r^{2}}{2}]}_{r = 0}^{r = 4} d θ \\ = & 8 \int_{0}^{2 π} d θ \\ = & 16 π . \end{aligned}

Fortunately, this is the same answer that we found in Example 5.8.5, as it should!

🔗

Example 5.8.8. Using Stokes' theorem to evaluate a line integral by transforming it into a surface integral.

Use Stokes' theorem to evaluate the line integral of the one-form $ω = x y d x + y z d y + z^{4} d z$ over the curve $C$ that forms the boundary of the part of the paraboloid $z = 1 - x^{2} - y^{2}$ with $x \geq 0,$ $y \geq 0,$ $z \geq 0 .$ Assume that $C$ is given the orientation as moving from the $x$ -axis to the $y$ -axis to the $z$ -axis.

It may be hard to visualize the curve and the region at first. A picture is worth a thousand words. Here is a figure representing the part of the paraboloid $z = 1 - x^{2} - y^{2}$ with $x \geq 0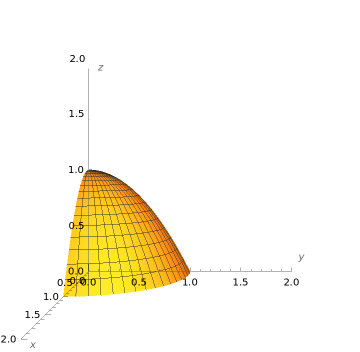,$ $y \geq 0,$ $z \geq 0 .$

We want to evaluate the line integral of $ω$ along the boundary $C$ of this region. We could evaluate the line integral directly. Or we can use Stokes' theorem, which says that

\int_{C} ω = \int_{S} d ω,

where $S$ is the part of the paraboloid described above. We need to be careful with orientation here. We assume that $C$ is oriented going from $x$ to $y$ to $z .$ Looking at the figure, we see that if we walk along the boundary curve in this direction, to keep the surface on the left we must have our heads pointing away from the origin. So the surface $S$ should be oriented with a normal vector pointing in that direction.

To evaluate the surface integral of $d ω$ along $S,$ we first calculate the exterior derivative. We get:

d ω = x d y \land d x + y d z \land d y .

Next, we parametrize the surface $S$ as $α : D \to R^{3},$ with

D = {(r, θ) \in R^{2} | r \in [0, 1], θ \in [0, π / 2]}

and

α (r, θ) = (r \cos (θ), r \sin (θ), 1 - r^{2}) .

The region $D$ was chosen such that $x (r, θ), y (r, θ), z (r, θ) \geq 0$ on $D .$ Thus it covers the part of the paraboloid that we are interested in.

The normal vector is

\begin{aligned} n = & T_{r} \times T_{θ} \\ = & (\cos (θ), \sin (θ), - 2 r) \times (- r \sin (θ), r \cos (θ), 0) \\ = & (2 r^{2} \cos (θ), 2 r^{2} \sin (θ), r) . \end{aligned}

As its $z$ -component is positive, we see that it points away from the origin, as it should. So the orientation induced by the parametrization is the correct one.

Finally, we calculate the pullback of the two-form $d ω :$

\begin{aligned} α^{*} (d ω) = & r \cos (θ) (\sin (θ) d r + r \cos (θ) d θ) \land (\cos (θ) d r \\ - r \sin (θ) d θ) + r \sin (θ) (- 2 r d r) \land (\sin (θ) d r + r \cos (θ) d θ) \\ = & (- r^{2} \cos (θ) - 2 r^{3} \sin (θ) \cos (θ)) d r \land d θ . \end{aligned}

We then evaluate the surface integral:

\begin{aligned} \int_{α} d ω = & \int_{D} α^{*} (d ω) \\ = & \int_{0}^{π / 2} \int_{0}^{1} (- r^{2} \cos (θ) - 2 r^{3} \sin (θ) \cos (θ)) d r d θ \\ = & \int_{0}^{π / 2} {[- \frac{r^{3}}{3} \cos (θ) - \frac{r^{4}}{2} \sin (θ) \cos (θ)]}_{r = 0}^{r = 1} d θ \\ = & \int_{0}^{π / 2} (- \frac{1}{3} \cos (θ) - \frac{1}{2} \sin (θ) \cos (θ)) d θ \\ = & - \frac{1}{3} - \frac{1}{4} \\ = & - \frac{7}{12} . \end{aligned}

Therefore, by Stokes' theorem, the lintegral of $ω$ along $C$ is

\int_{C} ω = - \frac{7}{12} .

It is a good exercise to evaluate the line integral directly along the boundary curve (which you will need to split into three parametric curves). You should get the same answer $- 7 / 12 .$ And, as complicated as the calculation above looked, it is actually simpler than calculating the line integral directly!

🔗

Remark 5.8.10.

We can also use Stokes' theorem to show that a two-form is not exact, by showing that its surface integral along a closed surface does not vanish. This is similar to what we did for one-forms using the Fundamental Theorem of line integrals, see Exercise 3.4.3.2 (and also Exercise 5.7.3.5 ). We use Stokes' theorem in this way in Exercise 5.8.3.5 for the two-form in Remark 4.6.6.

🔗

Subsection 5.8.2 Stokes' theorem in terms of vector fields

🔗

As usual we translate Stokes' theorem in terms of the associated vector fields, as in Corollary 5.6.5.

🔗

Theorem 5.8.11. Stokes' theorem for vector fields.

Let $F$ be a smooth vector field on $U \subseteq R^{3} .$ Let $α : D \to R^{3}$ be a parametric surface whose image surface $S = α (D) \subset U$ is orientable and oriented by parametrization, with oriented boundary $\partial α .$ Then Stokes' theorem is the statement that

\iint_{S} (\nabla \times F) \cdot d S = \int_{\partial S} F \cdot d r,

where on the left-hand-side we used the shorthand notation introduced in Remark 5.6.6 to denote the surface integral of the vector field $\nabla \times F$ along the oriented parametric surface $S,$ and on the right-hand-side we use the shorthand notation from Remark 3.3.8 to denote the line integral of the vector field $F$ along the oriented boundary curve $\partial S$ parametrized by $r .$

🔗

From Corollary 5.8.2 and Corollary 5.8.3, we conclude that:

The surface integral of the curl of a vector field is the same for any two surfaces that share the same oriented boundary.
The surface integral of the curl of a vector field along a closed surface always vanishes.

🔗

As before, we can use Stokes' theorem in both directions. For instance, if we are interested in calculating the line integral of a vector field along a closed curve in

R^{3}

(say, to calculate the work done by a force field on an object moving along the closed curve), then we can use Stokes' theorem, which tells us that that the line integral is equal to the surface integral of the curl of the vector field on any surface whose boundary is the closed curve. In particular, we are free to choose a surface that is simple enough so that the resulting surface integral is easy to evaluate.

🔗

Exercises 5.8.3 Exercises

🔗

1.

Let $S$ be the part of the cone $z = 2 \sqrt{x^{2} + y^{2}}$ below the plane $x + z = 1,$ oriented with an upward normal vector. Let $S^{'}$ be the part of the plane $x + z = 1$ contained within the cone $z = 2 \sqrt{x^{2} + y^{2}},$ also oriented with an upward normal vector. Let $η$ be the one-form

η = e^{x^{2}} d x + e^{y^{3}} d y + 5 (x + z - 1)^{2} d z .

Use Stokes' theorem to show that

\int_{S} d η = 0.

Solution.

First, the oriented boundary of $S$ is the closed curve at the intersection of the cone $z = 2 \sqrt{x^{2} + y^{2}}$ and the plane $x + z = 1,$ oriented counterclockwise (looking from above). We notice that the boundary of $S^{'}$ is exactly the same. Therefore, by Stokes' theorem, we know that

\int_{S} d η = \int_{S^{'}} d η .

So we may as well evaluate the integral of $d η$ along the surface $S^{'},$ which lies within the plane $x + z = 1 .$

To do so, we need to evaluate the exterior derivative $d η .$ We get:

\begin{aligned} d η = & d (e^{x^{2}}) \land d x + d (e^{y^{3}}) \land d y + 5 d ((x + z - 1)^{2}) \land d z \\ = & 10 (x + z - 1) d x \land d z . \end{aligned}

To evaluate the surface integral $\int_{S^{'}} d η,$ we would need to parametrize the surface $S^{'},$ pullback $d η,$ and evaluate the integral as a double integral. However, we can show that the integral will be zero right away without going through the whole calculation. Indeed, when we pullback $d η$ by the parametrization, we need to evaluate its component function on the surface. But the surface $S^{'}$ lies within the plane $x + z = 1,$ and we see right away that the component function vanishes when $x + z - 1 .$ In other words, the two-form $d η = 0$ when restricted to the plane $x + z = 1 .$ So it will certainly vanish on $S^{'} .$ Therefore, we can conclude right away that

\int_{S^{'}} d η = 0,

and, by Stokes' theorem,

\int_{S} d η = 0.

🔗

2.

Consider the force field

F (x, y, z) = (- y x^{2} + z, x y^{2}, e^{x y} + z) .

Use Stokes' theorem to find the work done by the force field when moving an object counterclockwise along the circle $x^{2} + y^{2} = 4$ in the plane $z = 10 .$

Solution.

Let $\partial S$ be the circle $x^{2} + y^{2} = 4$ in the plane $z = 10$ with counterclockwise orientation, and let $S$ be the disk $x^{2} + y^{2} \leq 4$ within the plane $z = 10,$ with orientation given by an upward pointing normal vector. By Stokes' theorem, we know that

\int_{\partial S} F \cdot d r = \iint_{S} (\nabla \times F) \cdot d S .

So instead of evaluating the line integral of $F$ along $\partial S,$ we can evaluate the surface integral of the curl of $F$ along $S .$

First, we calculate the curl of $F .$ We get:

\nabla \times F = (x e^{x y}, 1 - y e^{x y}, y^{2} + x^{2}) .

To calculate the surface integral, we need to parametrize the surface $S .$ We use the following parametrization: $α : D \to R^{3},$ with

D = {(r, θ) \in R^{2} | r \in [0, 2], θ \in [0, 2 π]},

with

α (r, θ) = (r \cos (θ), r \sin (θ), 10) .

The tangent vectors are

T_{r} = (\cos (θ), \sin (θ), 0), T_{θ} = (- r \sin (θ), r \cos (θ), 0) .

The normal vector is

n = T_{r} \times T_{θ} = (0, 0, r),

which points upward as required. Therefore, the surface integral is

\begin{aligned} \iint_{S} (\nabla \times F) \cdot d S = & \iint_{D} (\nabla \times F) (α (r, θ)) \cdot n d A \\ = & \iint_{D} (r \cos (θ) e^{r^{2} \sin (θ) \cos (θ)}, 1 - r \sin (θ) e^{r^{2} \sin (θ) \cos (θ)}, r^{2}) \cdot (0, 0, r) d A \\ = & \iint_{D} r^{3} d A \\ = & \int_{0}^{2 π} \int_{0}^{2} r^{3} d r d θ \\ = & 4 \int_{0}^{2 π} d θ \\ = & 8 π . \end{aligned}

Therefore, by Stokes' theorem we conclude that the work done by the force field when moving an object counterclockwise along the circle $\partial S$ is $8 π .$

🔗

3.

Let $S$ be the surface consisting of the top and the four sides (but not the bottom) of the cube with vertices $(\pm 1, \pm 1, \pm 1)$ in $R^{3},$ with orientation given by an outward pointing normal vector, and $F$ the vector field

F = (x y, z x, \cos (x^{2}) + z^{5}) .

Use Stokes' theorem to evaluate the surface integral

\iint_{S} (\nabla \times F) \cdot d S .

Solution.

We can use Stokes' theorem in two different ways here: either to rewrite the surface integral as a line integral, or to rewrite it as a surface integral over a simpler surface. For completeness I will do it both ways.

First, we can use Stokes' theorem to rewrite the surface integral as a line integral. Let us do this first. We notice that the boundary curve $\partial S$ of the surface $S$ is the square with vertices $(\pm 1, \pm 1, - 1),$ since the bottom side of the cube is not included in $S .$ The induced orientation on the boundary amounts to moving counterclockwise along the square, as seen from above. Thus, by Stokes' theorem, we know that

\iint_{S} (\nabla \times F) \cdot d S = \int_{\partial S} F \cdot d r,

where the right-hand-side is the line integral of the vector field $F$ along the square with counterclockwise orientation.

To evaluate the line integral, we split the square into four line segments $L_{i},$ $i = 1, \dots, 4 .$ We parametrize the line segments by $α_{i} : [0, 1] \to R^{3}$ with

\begin{aligned} α_{1} (t) = & (- 1 + 2 t, - 1, - 1), \\ α_{2} (t) = & (1, - 1 + 2 t, - 1), \\ α_{3} (t) = & (1 - 2 t, 1, - 1), \\ α_{4} (t) = & (- 1, 1 - 2 t, - 1) . \end{aligned}

We calculate the tangent vectors:

\begin{matrix} T_{1} = (2, 0, 0), \\ T_{2} = (0, 2, 0), \\ T_{3} = (- 2, 0, 0), \\ T_{4} = (0, - 2, 0) . \end{matrix}

We finally evaluate the line integrals:

\begin{aligned} \int_{L_{1}} F (α_{1} (t)) \cdot T_{1} d t = & 2 \int_{0}^{1} (- 1 + 2 t) (- 1) d t = 0, \\ \int_{L_{2}} F (α_{2} (t)) \cdot T_{2} d t = & 2 \int_{0}^{1} (- 1) (1) d t = - 2, \\ \int_{L_{3}} F (α_{3} (t)) \cdot T_{3} d t = & - 2 \int_{0}^{1} (1 - 2 t) (1) d t = 0, \\ \int_{L_{4}} F (α_{4} (t)) \cdot T_{4} d t = & - 2 \int_{0}^{1} (- 1) (- 1) / d t = - 2. \end{aligned}

Adding up these four line integrals, we get $- 4 .$ We conclude, by Stokes' theorem, that the surface integral

\iint_{S} (\nabla \times F) \cdot d S = - 4.

Another approach would have been to use Stokes' theorem to rewrite the surface integral as a simpler surface integral. For instance we could have replaced the surface $S$ by the missing side of the cube (namely the bottom), as it shares the same boundary with $S .$ Let us call the bottom side of the cube $S^{'} .$ If we give it an upward pointing normal vector, it induces the same orientation on the boundary as $S .$ Thus, by Stokes' theorem,

\iint_{S} (\nabla \times F) \cdot d S = \iint_{S^{'}} (\nabla \times F) \cdot d S^{'} .

To evaluate the integral on the right-hand-side, we first calculate the curl of $F .$ We get:

\nabla \times F = (- x, 2 x \sin (x^{2}), z - x) .

Next, we need to parametrize $S^{'},$ which is the square with vertices $(\pm 1, \pm 1, - 1) .$ We write $α : D \to R^{3}$ with

D = {(u, v) \in R^{2} | u \in [- 1, 1], v \in [- 1, 1]},

and

α (u, v) = (u, v, - 1) .

The tangent vectors are

T_{u} = (1, 0, 0), T_{v} = (0, 1, 0),

with normal vector

n = T_{u} \times T_{v} = (0, 0, 1) .

This is the correct orientation. We thus have

\begin{aligned} \iint_{S^{'}} (\nabla \times F) \cdot d S^{'} = & \int_{- 1}^{1} \int_{- 1}^{1} (- u, 2 u \sin (u^{2}), - 1 - u) \cdot (0, 0, 1) d u d v \\ = & - \int_{- 1}^{1} \int_{- 1}^{1} (u + 1) d u d v \\ = & - 4. \end{aligned}

The same answer as before!

🔗

4.

Let $C \subset R^{2}$ be a simple closed curve, and $D \subset R^{2}$ the region consisting of $C$ and its interior. Let $α : D \to R^{3}$ be the parametric surface

α (u, v) = (u, v, 1 - u - v),

with $S = α (D)$ and $\partial S$ the boundary curve of $S .$ Let $η$ be the one-form

η = - z d x - 2 x d y + 4 y d z .

Use Stokes' theorem to show that the line integral of $η$ along $\partial S$ is equal to the area of the region $D \subset R^{2} .$

Solution.

First, by Stokes' theorem we know that

\int_{\partial α} η = \int_{α} d η,

with the orientation induced by the parametrization. To evaluate the integral on the right-hand-side, we calculate the exterior derivative:

d η = - d z \land d x - 2 d x \land d y + 4 d y \land d z .

We calculate its pullback:

\begin{aligned} α^{*} (d η) = & - (- d u - d v) \land d u - 2 d u \land d v + 4 d v \land (- d u - d v) \\ = & d u \land d v . \end{aligned}

Therefore, the surface integral becomes

\begin{aligned} \int_{α} d η = & \int_{D} α^{*} (d η) \\ = & \int_{D} d u \land d v, \end{aligned}

which is simply the area of the region $D .$ We then conclude, by Stokes' theorem, that the line integral of $η$ along $\partial S$ is equal to the area of the region $D .$

🔗

5.

Consider the two-form

ω = \frac{1}{(x^{2} + y^{2} + z^{2})^{3 / 2}} (x d y \land d z + y d z \land d x + z d x \land d y),

from Remark 4.6.6. It is defined on $U = R^{3} ∖ {(0, 0, 0)} .$

Show that $ω$ is closed, that is, $d ω = 0 .$
Show that $ω$ is not exact by showing that the surface integral of $ω$ along the sphere $x^{2} + y^{2} + z^{2} = 1$ is non-zero.
Does that contradict Poincare's theorem for two-forms?

Solution.

(a) To show that it is closed, we calculate the exterior derivative. We get:

\begin{aligned} d ω = & (\frac{(x^{2} + y^{2} + z^{2})^{3 / 2} - 3 x^{2} (x^{2} + y^{2} + z^{2})^{1 / 2}}{(x^{2} + y^{2} + z^{2})^{3}} \\ + \frac{(x^{2} + y^{2} + z^{2})^{3 / 2} - 3 y^{2} (x^{2} + y^{2} + z^{2})^{1 / 2}}{(x^{2} + y^{2} + z^{2})^{3}} \\ + \frac{(x^{2} + y^{2} + z^{2})^{3 / 2} - 3 z^{2} (x^{2} + y^{2} + z^{2})^{1 / 2}}{(x^{2} + y^{2} + z^{2})^{3}}) d x \land d y \land d z \\ = & \frac{1}{(x^{2} + y^{2} + z^{2})^{5 / 2}} (3 (x^{2} + y^{2} + z^{2}) - 3 (x^{2} + y^{2} + z^{2})) d x \land d y \land d z \\ = & 0. \end{aligned}

Therefore, $ω$ is closed.

(b) In fact, we already did such a surface integral in Exercise 5.6.4.5, but for completeness we redo it here. We parametrize the sphere as always with spherical coordinates, $α : D \to R^{3},$

D = {(θ, ϕ) \in R^{2} | θ \in [0, π], ϕ \in [0, 2 π]},

and

α (θ, ϕ) = (\sin (θ) \cos (ϕ), \sin (θ) \sin (ϕ), \cos (θ)) .

The pullback of $ω$ is:

\begin{aligned} α^{*} ω = & \frac{1}{1} (\sin (θ) \cos (ϕ) (\cos (θ) \sin (ϕ) d θ + \sin (θ) \cos (ϕ) d ϕ) \land (- \sin (θ) d θ) \\ + \sin (θ) \sin (ϕ) (- \sin (θ) d θ)) \land (\cos (θ) \cos (ϕ) d θ) - \sin (θ) \sin (ϕ) d ϕ) \\ + \cos (θ) (\cos (θ) \cos (ϕ) d θ) - \sin (θ) \sin (ϕ) d ϕ) \land (\cos (θ) \sin (ϕ) d θ + \sin (θ) \cos (ϕ) d ϕ)) \\ = & (\sin^{3} (θ) \cos^{2} (ϕ) + \sin^{3} (θ) \sin^{2} (ϕ) + \sin (θ) \cos^{2} (θ)) d θ \land d ϕ \\ = & \sin (θ) d θ \land d ϕ . \end{aligned}

We finally calculate the surface integral:

\begin{aligned} \int_{α} ω = & \int_{D} α^{*} ω \\ = & \int_{0}^{2 π} \int_{0}^{π} \sin (θ) d θ d ϕ \\ = & 2 \int_{0}^{2 π} d ϕ \\ = 4 π . \end{aligned}

The result is certainly non-zero!

As the surface integral of $ω$ along the sphere is non-zero, we conclude that $ω$ cannot be exact, since we know from Stokes' theorem that the surface of integral of an exact two-form along a closed surface must vanish.

(c) We have shown that $ω$ is a closed two-form that is not exact. But it does not contradict the statement of Poincare's lemma for two-forms, see Theorem 4.6.4, since $ω$ is not defined on all of $R^{3};$ it is not defined at the origin. It also does not contradict version II of Poincare's lemma that we saw in Theorem 4.6.5, since $ω$ is also not defined on an open ball (the origin is missing).

🔗

6.

Let $F$ be a smooth vector field on $R^{3}$ and $f$ a smooth function on $R^{3} .$ Let $α : D \to R^{3}$ be a parametric surface. Show that

\iint_{α} (f \nabla \times F) \cdot d S = - \iint_{α} (\nabla f \times F) \cdot d S + \int_{\partial α} f F \cdot d r .

Solution.

The key here is recall some of the vector calculus identities that we encountered previously. From Lemma 4.4.9, we know that

\nabla \times (f F) = (\nabla f) \times F + f \nabla \times F .

From the point of view of differential forms, this identity follows from the graded product rule for the exterior derivative.

Using this identity, we can write:

\iint_{α} (f \nabla \times F) \cdot d S = - \iint_{α} (\nabla f) \times F + \iint_{α} \nabla \times (f F) .

The second term on the right-hand-side is the surface integral of the curl of the vector field $f F .$ Using Stokes' theorem, we can rewrite it as a line integral:

\iint_{α} \nabla \times (f F) = \int_{\partial α} f F \cdot d r .

Therefore, we conclude that

\iint_{α} (f \nabla \times F) \cdot d S = - \iint_{α} (\nabla f) \times F + \int_{\partial α} f F \cdot d r .