Skip to main content

Section 4.5 Physical interpretation of grad, curl, div

In this section we pause for a moment and explore further the physical interpretation of the vector calculus operations of gradient, curl, and divergence.

Subsection 4.5.1 The gradient of a function

Let \(f: U \to \mathbb{R}\) be a smooth function with \(U \subseteq \mathbb{R}^3\text{.}\) We start by reviewing the interpretation of the gradient

\begin{equation*} \boldsymbol{\nabla} f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right)\text{,} \end{equation*}

which as we saw is the vector field associated to the exterior derivative \(d f\text{.}\) At a point \(p \in U\text{:}\)

  • The direction of the gradient is the direction in which the function \(f\) increases most quickly at \(p\text{;}\)

  • The magnitude of the gradient is the rate of fastest increase at \(p\text{.}\)

This may be most easily understood with an example.

In this example we work with a function on \(\mathbb{R}^2\) instead of \(\mathbb{R}^3\text{,}\) but the interpretation is the same.

Suppose that the function \(H(x,y) = -x^2-y^2+1000\) gives the height above sea level at point \((x,y)\) on a surface. The height is highest at the origin, where \(H(0,0) = 1000\text{,}\) and decreases as we move away from the origin, until it reaches sea level on the circle with radius \(\sqrt{1000}\text{.}\) So we can think of this altitude function as representing in a circular mountain centred at the origin.

The level curves of \(H\) are the curves of constant elevation, i.e.

\begin{equation*} H(x,y) = - x^2 - y^2 + 1000 = C \qquad \Leftrightarrow \qquad x^2+y^2 = 1000-C \end{equation*}

for constant elevations \(0 \leq C \leq 1000\text{.}\) Those would correspond to the level curves of elevation on a topographical map. In this case, they are all circles centred at the origin.

The gradient of \(H\) is

\begin{equation*} \boldsymbol{\nabla} H = \left( \frac{\partial H}{\partial x}, \frac{\partial H}{\partial y} \right) = - 2 ( x, y). \end{equation*}

For any point \((x,y)\) on the surface, this is a vector that points towards the origin, which says that the direction of steepest increasing slope is towards the origin, as expected from a circular mountain centred at the origin. Moreover, we see that the magnitude of the gradient vector is

\begin{equation*} |\boldsymbol{\nabla} H| = 2 \sqrt{x^2+y^2}. \end{equation*}

This says that the slope is steeper far away from the origin, and becomes less and less steep as we get closer to the origin.

Here is below the contour map for this function (the graph of its level curves), and also a 3D plot (both produced using Mathematica).

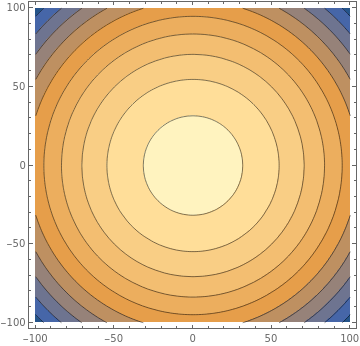
A contour map of the function \(H(x,y) = - x^2 - y^2 + 1000\text{,}\) for \(-100 \leq x \leq 100\) and \(-100 \leq y \leq 100\text{.}\)
Figure 4.5.2. A contour map of the function \(H(x,y) = - x^2 - y^2 + 1000\text{,}\) for \(-100 \leq x \leq 100\) and \(-100 \leq y \leq 100\text{.}\)
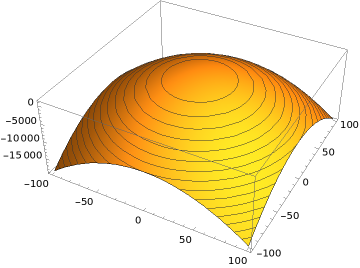
A 3d plot of the function \(z = - x^2 - y^2 + 1000\) (i.e. thinking of \(H(x,y)\) as representing the height of the surface above sea level), for \(-100 \leq x \leq 100\) and \(-100 \leq y \leq 100\text{.}\)
Figure 4.5.3. A 3d plot of the function \(z = - x^2 - y^2 + 1000\) (i.e. thinking of \(H(x,y)\) as representing the height of the surface above sea level), for \(-100 \leq x \leq 100\) and \(-100 \leq y \leq 100\text{.}\)

Subsection 4.5.2 The curl of a vector field

Let \(\mathbf{F}: U \to \mathbb{R}^3\) be a smooth vector field with \(U \subseteq \mathbb{R}^3\text{,}\) with component functions \(\mathbf{F} = (f_1, f_2, f_3)\text{.}\) Its curl is given by the vector field

\begin{equation*} \boldsymbol{\nabla} \times \mathbf{F} = \left( \frac{\partial f_3}{\partial y} - \frac{\partial f_2}{\partial z} , \frac{\partial f_1}{\partial z} - \frac{\partial f_3}{\partial x}, \frac{\partial f_2}{\partial x} - \frac{\partial f_1}{\partial y} \right) . \end{equation*}

What is it actually computing? How can we interpret the vector field \(\boldsymbol{\nabla} \times \mathbf{F}\text{?}\)

It is easiest to understand the meaning of the curl of a vector field by thinking of \(\mathbf{F}(x,y,z)\) as the velocity field of a moving fluid in three dimensions. So let us call it \(\mathbf{v}(x,y,z)\) instead. The curl is related to rotational motion induced by the fluid.

Consider an infinitesimally small ball (sphere) located within the fluid, and centered at a point \(p \in U\text{.}\) Assume that the ball has a rough surface. The fluid moving around the ball will generally make it rotate. Then:

  • The direction of the curl \(\boldsymbol{\nabla} \times \mathbf{v}\) at \(p\) gives the axis of rotation (according to the right hand rule); 1 

  • Half the magnitude of the curl \(\boldsymbol{\nabla} \times \mathbf{v}\) at \(p\) gives the angular speed of rotation.

The “right hand rule” means that if you align the thumb of your right hand along the vector, the fingers of your right hand will “curl” around the axis of rotation in the direction of rotation.

In particular, if \(\boldsymbol{\nabla} \times \mathbf{v} = 0\) at a point \(p\text{,}\) the fluid does not cause the sphere centered at \(p\) to rotate. Because of this interpretation, we say that the velocity field of a fluid is irrotational if it is curl-free at all points on \(U\text{,}\) that is \(\boldsymbol{\nabla} \times \mathbf{v}=0\) on \(U\text{.}\)

Suppose that a moving fluid has velocity field given by

\begin{equation*} \mathbf{v}(x,y,z) = (- y , x , 0). \end{equation*}

Sketching the vector field (see Exercise 2.1.3.2), one sees that at any point, the fluid is rotating counterclockwise around the \(z\)-axis. Using the right-hand-rule, we thus expect the curl \(\boldsymbol{\nabla} \times \mathbf{v}\) to point in the positive \(z\)-direction, since it is the axis of rotation. We calculate:

\begin{equation*} \boldsymbol{\nabla} \times \mathbf{v} = \left( 0, 0, 2 \right). \end{equation*}

Indeed, it points in the positive \(z\)-direction, as expected. Furthermore, half the magnitude of the curl is

\begin{equation*} \frac{1}{2} | \boldsymbol{\nabla} \times \mathbf{v} | = 1, \end{equation*}

which means that the angular speed of rotation of the ball would be \(1\) radian per unit of time.

Conside a moving fluid with velocity field given by

\begin{equation*} \mathbf{v}(x,y,z) = (x,y,z). \end{equation*}

Sketching the vector field, we see that this would be a fluid in expansion. As the fluid is expanding, regardless of where the small sphere is located, it should not cause it to rotate (try to visualize this yourself). So we expect the velocity field to be curl-free. From the definition of the curl, we calculate:

\begin{equation*} \boldsymbol{\nabla} \times \mathbf{v} = (0,0,0). \end{equation*}

Thus it is curl-free, as expected, and this is an example of an irrotational velocity field.

Irrotational fluids do not have to be necessarily spherically symmetric. Consider for instance a moving fluid with velocity field

\begin{equation*} \mathbf{v}(x,y,z) = (0,0,1). \end{equation*}

This would be a fluid that is moving uniformly in the positive \(z\)-direction. If you think about it for a little bit, it should not induce any rotation either, regardless of where the small sphere is located. So we expect the velocity field to be curl-free again. Indeed, from the definition we \(\boldsymbol{\nabla} \times \mathbf{v} = (0,0,0)\text{,}\) which says that the velocity field is irrotational.

Subsection 4.5.3 The divergence of a vector field

Let \(\mathbf{F}: U \to \mathbb{R}^3\) be a smooth vector field with \(U \subseteq \mathbb{R}^3\text{,}\) with component functions \(\mathbf{F} = (f_1, f_2, f_3)\text{.}\) Its divergence is the function:

\begin{equation*} \boldsymbol{\nabla} \cdot \mathbf{F} = \frac{\partial f_1}{\partial x} + \frac{\partial f_2}{\partial y} + \frac{\partial f_3}{\partial z}. \end{equation*}

What is its intepretation?

As for the curl, it is easiest to interpret the divergence by thinking of the vector field as being the velocity field \(\mathbf{v}(x,y,z)\) of a moving fluid or gas. The divergence is then related to expansion and compression of the fluid.

More precisely, consider an infinitesimally small sphere around a point \(p \in U\text{:}\)

  • The divergence \(\boldsymbol{\nabla} \cdot \mathbf{v}\) at \(p\) measures the rate at which the fluid is exiting the small sphere at \(p\) (per unit of time and unit of volume).

The key here is that if the divergence at a point is positive, it means that more fluid is exiting the small sphere centered at this point then entering the sphere, and vice-versa if the divergence is negative. If it is zero, this means that the fluid may still be moving, but there is exactly the same amount of fluid entering and existing the sphere.

For instance, if a gas is heated, it will expand. This means that for any small sphere in the gas, there will be more gas exiting then entering. So the divergence will be positive everywhere. Conversely, if a gas is cooled, it will contract, and its divergence will be negative everywhere.

Motivated by this interpretation, we say that the velocity field of a fluid is incompressible if it is divergence-free everywhere, i.e. \(\boldsymbol{\nabla} \cdot \mathbf{v} = 0\) everywhere on \(U\text{.}\) We also call such vector fields solenoidal.

Consider a fluid/gas with velocity field

\begin{equation*} \mathbf{v}(x,y,z) = (x,y,z). \end{equation*}

The velocity field is pointing outwards in all directions. This corresponds to an expanding fluid. If we first think of a small sphere centered at the origin, then the fluid is moving outwards in all directions, exiting the sphere, and thus we expect the divergence to be positive. In fact, even if the small sphere is located elsewhere, we still expect the divergence to be positive, as there will be more fluid exiting the sphere than entering the sphere. From the definition, we calculate

\begin{equation*} \boldsymbol{\nabla} \cdot \mathbf{v} = 1+1+1 = 3, \end{equation*}

which is indeed positive everywhere, as expected.

Consider a fluid with velocity field

\begin{equation*} \mathbf{v}(x,y,z) = (-y,x,0). \end{equation*}

As we have seen (see Exercise 2.1.3.2), the fluid is rotating counterclockwise around the \(z\)-axis. It is not so obvious to see whether more fluid is existing or entering small spheres in the fluid.

It is easiest to consider first a sphere centered around the origin. Because of the rotational motion, we see that actually no fluid is entering or leaving the sphere at all. So we expect the divergence to be zero, at least at the origin.

It is not so obvious to see why the same should be true for all spheres not centered at the origin, but you can try to visualize it. In the end, through direct calculation, we get that \(\boldsymbol{\nabla} \cdot \mathbf{v} = 0\text{,}\) and hence the velocity field is divergence-free (that is, incompressible).

Consider the fluid with velocity field

\begin{equation*} \mathbf{v}(x,y,z) = (0,0,1), \end{equation*}

which has uniform velocity in the positive \(z\)-direction. Here, if you pick a small sphere centered anywhere, there is certainly fluid entering and exiting the sphere because of the linear motion of the fluid, but the exact same amount of fluid will enter and exit the sphere. Therefore we expect the divergence to be zero everywhere, and indeed, \(\boldsymbol{\nabla} \cdot \mathbf{v} = 0\text{.}\) Another example of an incompressible velocity field.

Comparing with Example 4.5.6, we see that this velocity field is both irrotational and incompressible, since it is both curl-free and divergence-free.

Exercises 4.5.4 Exercises

1.

Show that any vector field of the form

\begin{equation*} \mathbf{F}(x,y,z) = \left( f(x), g(y), h(z) \right) \end{equation*}

is irrotational.

Solution.

To show that \(\mathbf{F}\) is irrotational, we need to show that

\begin{equation*} \boldsymbol{\nabla} \times \mathbf{F} = 0. \end{equation*}

We can use directly the formula for the curl, or we can use the language of differential forms. In the latter, we associate a one-form \(\omega\) to the vector field \(\mathbf{F}\text{:}\)

\begin{equation*} \omega = f(x)\ dx + g(y)\ dy + h(z)\ dz. \end{equation*}

We want to show that \(d \omega = 0\text{.}\) But this is clear true, as taking the exterior derivative gives

\begin{equation*} d \omega = \frac{df}{dx}\ dx \wedge dx + \frac{dg}{dy}\ dy \wedge dy + \frac{dh}{dz}\ dz \wedge dz =0, \end{equation*}

since \(f(x), g(y), h(z)\) are only functions of \(x,y,z\) respectively. Therefore \(\mathbf{F}\) is irrotational.

2.

Show that any vector field of the form

\begin{equation*} \mathbf{F}(x,y,z) = \left( f(y,z), g(x,z), h(x,y) \right) \end{equation*}

is incompressible.

Solution.

To show that \(\mathbf{F}\) is incompressible, we need to show that

\begin{equation*} \boldsymbol{\nabla} \cdot \mathbf{F} = 0. \end{equation*}

This is the statement that

\begin{equation*} \frac{\partial f}{\partial x} + \frac{\partial g}{\partial y} + \frac{\partial h}{\partial z} = 0. \end{equation*}

But each of those partial derivatives vanishes, since \(f(y,z)\) does not depend on \(x\text{,}\) \(g(x,z)\) does not depend on \(y\text{,}\) and \(h(x,y)\) does not depend on \(z\text{.}\) Therefore \(\mathbf{F}\) is incompressible.

3.

Consider a vector field \(\mathbf{F}(x,y,z) = (f_1(x,y), f_2(x,y), 0)\) on \(\mathbb{R}^3\text{;}\) it is independendent of \(z\text{,}\) and its \(z\)-component is zero. A sketch of the vector field in the \(xy\)-plane is shown in the figure below; as it is independent of \(z\text{,}\) it looks the same in all other horizontal planes.

  1. Is \(\boldsymbol{\nabla} \cdot \mathbf{F}\) positive, negative, or zero at the origin? What about at the point \((5,0,0)\text{?}\) And \((-5,0,0)\text{?}\)

  2. Is \(\boldsymbol{\nabla} \times \mathbf{F} = 0\) at the origin? If not, in what direction does it point?

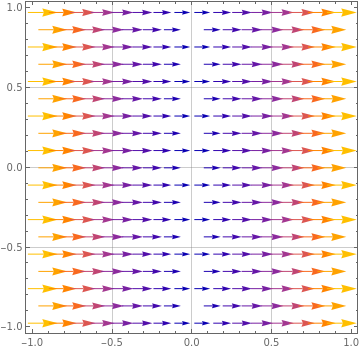
A sketch of the vector field \(\mathbf{F}\) in the \(xy\)-plane.
Figure 4.5.10. A sketch of the vector field \(\mathbf{F}\) in the \(xy\)-plane.
Solution.

(a) First we see that all arrows point in the positive \(x\)-direction. The lengths of the arrows appear to be symmetric about the \(y\)-axis. The arrows get longer and longer as you move away from the \(y\)-axis.

If you picture a small sphere around the origin, then there is fluid entering and leaving the sphere, and the arrows of the vectors entering and exiting have the same length. So you expect the divergence to be zero at the origin. In fact, the same is true for all points on the \(y\)-axis, i.e. with \(x=0\text{.}\)

At the point \((5,0,0)\text{,}\) there are arrows entering and leaving the sphere as well. But the arrows that leave the sphere are longer than those that enter, so there should be more fluid exiting than entering. So we expect the divergence to be positive. This should be the case for all points \((x,y)\) with \(x > 0\text{.}\)

As for \((-5,0,0)\text{,}\) the opposite happens; the arrows entering the sphere are longer than those leaving. So there should be more fluid entering than leaving, and we expect the divergence to be negative. The same is true for all points \((x,y)\) with \(x \lt 0\text{.}\)

(b) At the origin, the arrows are all pointing horizontally. As such, it will not induce any rotation on a sphere centered at the origin, and we expect the curl to be zero at the origin. In fact, this will be the case everywhere, so the curl should be zero everywhere.

For your interest, this is the vector field \(\mathbf{F}(x,y,z) = (x^2,0,0)\text{.}\) Its divergence is \(\boldsymbol{\nabla}\cdot \mathbf{F} = 2 x\text{.}\) We see that it is zero when \(x =0\text{,}\) positive for all \(x > 0\text{,}\) and negative for all \(x \lt 0\text{,}\) as expected. The curl is \(\boldsymbol{\nabla} \times \mathbf{F} = (0,0,0),\) which vanishes as expected (the vector field is irrotational).

4.

Consider a vector field \(\mathbf{F}(x,y,z) = (f_1(x,y), f_2(x,y), 0)\) on \(\mathbb{R}^3\text{;}\) it is independendent of \(z\text{,}\) and its \(z\)-component is zero. A sketch of the vector field in the \(xy\)-plane is shown in the figure below; as it is independent of \(z\text{,}\) it looks the same in all other horizontal planes.

  1. Is \(\boldsymbol{\nabla} \cdot \mathbf{F}\) positive, negative, or zero at the origin? What about at \((0,5,0)\text{?}\)

  2. Is \(\boldsymbol{\nabla} \times \mathbf{F} = 0\) at the origin? If not, in what direction does it point?

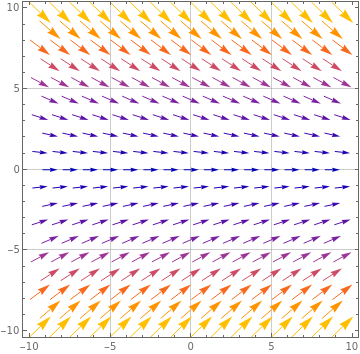
A sketch of the vector field \(\mathbf{F}\) in the \(xy\)-plane.
Figure 4.5.11. A sketch of the vector field \(\mathbf{F}\) in the \(xy\)-plane.
Solution.

(a) We look at a small sphere around the origin, and we want to know whether there is more or less fluid entering the sphere versus exiting the sphere. Around the origin, we see that the arrows appear to be the same length on both sides of the \(y\)-axis, and on both sides of the \(x\)-axis. The arrows are all pointing the positive \(x\)-direction. Furthermore, the arrows above the \(x\)-axis point downwards, while the arrows below the \(x\)-axis point upwards, in a symmetric way. If you think about it, this means that there is more fluid entering the sphere than exiting (because the arrows above and below the \(x\)-axis are pointing towards the \(x\)-axis). We thus expect the divergence to be negative at the origin.

At the point \((0,5,0)\text{,}\) the fluid is moving downwards, and the arrows appear to be bigger for \(y >5\) than for \(y \lt 5\text{.}\) So it looks like there is still more fluid entering the sphere than exiting the sphere. So we expect the divergence to be negative at this point as well.

(b) At the origin, all arrows point in the positive \(x\)-direction. Furthermore, the arrows above the \(x\)-axis point downwards, while the arrows below the \(x\)-axis point upwards, in a symmetric way. Therefore, if you imagine a small sphere around the origin, the motion of the fluid would not induce any rotation. So we expect its curl to vanish.

For your interest, this is the vector field \(\mathbf{F}(x,y,z) = (10,-y,0)\text{.}\) Its divergence is \(\boldsymbol{\nabla} \cdot \mathbf{F} = - 1\text{,}\) which is negative everywhere. As for the curl, we get \(\boldsymbol{\nabla} \times \mathbf{F} = (0,0,0)\text{,}\) so it is zero everywhere (the vector field is irrotational).

5.

Consider a vector field \(\mathbf{F}(x,y,z) = (f_1(x,y), f_2(x,y), 0)\) on \(\mathbb{R}^3\text{;}\) it is independendent of \(z\text{,}\) and its \(z\)-component is zero. A sketch of the vector field in the \(xy\)-plane is shown in the figure below; as it is independent of \(z\text{,}\) it looks the same in all other horizontal planes.

  1. Is \(\boldsymbol{\nabla} \cdot \mathbf{F}\) positive, negative, or zero at the origin? What about at \((0,5,0)\text{?}\)

  2. Is \(\boldsymbol{\nabla} \times \mathbf{F} = 0\) at the origin? If not, in what direction does it point?

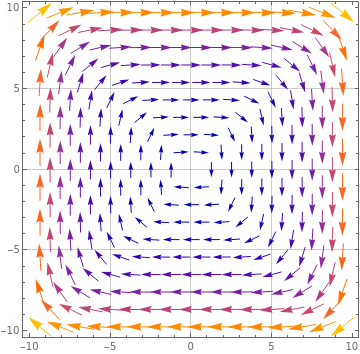
A sketch of the vector field \(\mathbf{F}\) in the \(xy\)-plane.
Figure 4.5.12. A sketch of the vector field \(\mathbf{F}\) in the \(xy\)-plane.
Solution.

(a) Arrows that are diametrically opposite around the origin appear to have the same length but point in opposite directions. As a result, the same amount of fluid should be entering and exiting a small sphere around the origin, and hence we expect the divergence to be zero at the origin.

As for the point \((0,5,0)\text{,}\) we see that at this point (just like for any point with \(x=0\)) all arrows are pointing horizontally. Furthermore, the length of the arrows on both sides of the \(y\)-axis appear to be the same, so we expect the same amount of fluid entering and exiting the sphere. Again, the divergence should be zero at this point.

(b) It is clear from the figure that the moving fluid would make a sphere centered at the origin rotate clockwise. We thus expect the curl to be non-zero at the origin. Using the right hand rule, we expect it to point in the negative \(z\)-direction. In fact, looking at the figure, we expect this to be true at all points. So we expect the divergence to be zero everywhere.

For your interest, this is the vector field \(\mathbf{F}(x,y,z) = (y^5, - x^5,0)\text{.}\) Its divergence is \(\boldsymbol{\nabla} \cdot \mathbf{F} = 0,\text{,}\) which is zero everywhere, as expected (the vector field is incompressible). Its curl is \(\boldsymbol{\nabla} \times \mathbf{F} = (0,0, - 5 x^4 - 5 y^4).\) We see that it points in the negative \(z\)-direction for all values of \(x,y\text{,}\) as expected.

6.

Consider a vector field \(\mathbf{F}(x,y,z) = (f_1(x,y), f_2(x,y), 0)\) on \(\mathbb{R}^3\text{;}\) it is independendent of \(z\text{,}\) and its \(z\)-component is zero. A sketch of the vector field in the \(xy\)-plane is shown in the figure below; as it is independent of \(z\text{,}\) it looks the same in all other horizontal planes.

  1. Is \(\boldsymbol{\nabla} \cdot \mathbf{F}\) positive, negative, or zero at the origin? What about at \((0,5,0)\text{?}\)

  2. Is \(\boldsymbol{\nabla} \times \mathbf{F} = 0\) at the origin? If not, in what direction does it point?

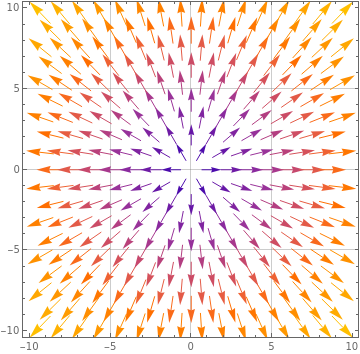
A sketch of the vector field \(\mathbf{F}\) in the \(xy\)-plane.
Figure 4.5.13. A sketch of the vector field \(\mathbf{F}\) in the \(xy\)-plane.
Solution.

(a) We see that all arrows point away from the origin, in a way that is spherically symmetric (the lengths of all arrows on a circle of a fixed radius about the origin appear to be the same). As such, the fluid is all exiting the sphere, so we expect the divergence to be positive at the origin.

At the point \((0,5,0)\text{,}\) there are arrows coming in and arrows coming out, but the arrows coming out are longer than the arrows coming out, so we expect again the divergence to be positive since more fluid is exiting the sphere than entering. In fact, this will be the case at all points in the figure. So we expect the divergence to be always positive.

(b) At the origin, the fluid is all pushing outwards in spherically symmetric way, so it will induce no rotation on a sphere centered at the origin. We thus expect the curl to be zero at the origin. While it may not be as obvious, you can probably convince yourself that this should be true at all points in the figure, so the curl should be zero everywhere.

For your interest, this is the vector field \(\mathbf{F}(x,y,z) = (x,y,0)\text{.}\) Its divergence is \(\boldsymbol{\nabla} \cdot \mathbf{F} = 2\text{,}\) which is positive everywhere, as expected. Its curl is \(\boldsymbol{\nabla} \times \mathbf{F} = (0,0,0)\text{,}\) which is zero everywhere as expected (the fuild is irrotational).