Skip to main content

Section 6.2 Divergence theorem in \(\mathbb{R}^3\)

We show that the generalized Stokes' theorem for a closed bounded region in \(\mathbb{R}^3\) reduces to the divergence theorem of vector calculus.

Subsection 6.2.1 Integrating a three-form over a region in \(\mathbb{R}^3\)

Our goal in this section is to study Stokes' theorem for two-/three-forms. As a first step we need to define integration of three-forms over regions in \(\mathbb{R}^3\text{,}\) just like we did for two-forms over regions in \(\mathbb{R}^2\) in Section 5.2 and Section 5.3.

In this section we concentrate on solid regions \(E \subset \mathbb{R}^3\) that consist of a closed surface and its interior, such as the regiong bounded by a sphere, or a rectangular box. We saw in Definition 5.2.1 how to define the orientation of \(\mathbb{R}^n\text{,}\) and in particular in Example 5.2.5 for \(\mathbb{R}^3\text{,}\) in which case it is given by a choice of right-handed or left-handed twirl, with right-handed twirl being the canonical orientation. We define the orientation of a region in \(\mathbb{R}^3\) as being induced from the orientation of the ambient space.

Definition 6.2.1. Orientation of a region in \(\mathbb{R}^3\) and induced orientation on the boundary.

Let \(E \subset \mathbb{R}^3\) be a solid region that consists of a closed surface and its interior. Its boundary \(\partial E\) is the closed surface. Choose an orientation on \(\mathbb{R}^3\text{.}\) We define the orientation of \(E\) as being the orientation induced by the ambient vector space \(\mathbb{R}^3\text{.}\) We write \(E_+\) for the region with the canonical (right-handed twirl) orientation, and \(E_-\) for the opposite (left-handed twirl) orientation.

If \(E\) is canonically oriented, we define the induced orientation on the boundary \(\partial E\) as corresponding to an outward pointing normal vector.

Let \(E \subset \mathbb{R}^3\) be the solid region in \(\mathbb{R}^3\) bounded by the sphere \(x^2+y^2+z^2 = R^2\text{.}\) Its boundary \(\partial E\) is the sphere itself, that is, the surface \(x^2+y^2+z^2=R^2\text{.}\) If we give \(E\) the canonical orientation given by a choice of ordered basis on \(\mathbb{R}^3\) corresponding to a right-handed twirl, then the induced orientation on the sphere is that of a normal vector pointing outward.

With this definition of orientation, we can define the integral of a three-form over a region in \(\mathbb{R}^3\text{.}\)

Definition 6.2.3. Integral of a three-form over a closed bounded region in \(\mathbb{R}^3\).

Let \(E \subset \mathbb{R}^3\) be a solid region that consists of a closed surface and its interior. Let \(\omega = f\ dx \wedge dy \wedge dz\) be a three-form on an open subset \(U \subseteq \mathbb{R}^3\) that contains \(E\text{.}\) If \(E\) has canonical orientation, we define the integral of \(\omega\) over \(E\) as:

\begin{equation*} \int_E \omega = \iiint_E f\ dV, \end{equation*}

where on the right-hand-side we mean the standard triple integral from calculus. If \(E\) has opposite orientation, we define

\begin{equation*} \int_E \omega = - \iiint_E f\ dV. \end{equation*}

Note that, as for the integral of two-forms over regions, the choice of basic three-form \(dx \wedge dy \wedge dz\) (which is consistent with the ordering of the canonical orientation) when expressing \(\omega\) in terms of the function \(f\) is important here, as integrals of three-forms are oriented, while triple integrals are not. (See Remark 5.3.5.)

The definition reduces the evaluation of integrals of three-forms to triple integrals, which you have encountered already in your previous calculus course. We will focus here on regions that are recursively supported, as we did for regions in \(\mathbb{R}^2\) (more general regions could be expressed as unions of recursively supported regions). We say that:

  1. A region \(E \subset \mathbb{R}^3\) is \(xy\)-supported (also called type 1) if there exists a region \(D\) in the \((x,y)\)-plane and two continuous functions \(z_1(x,y), z_2(x,y)\) such that

    \begin{equation*} E = \{(x,y,z) \in \mathbb{R}^3\ |\ (x,y) \in D, z_1(x,y) \leq z \leq z_2(x,y) \}. \end{equation*}

  2. A region \(E \subset \mathbb{R}^3\) is \(yz\)-supported (also called type 2) if there exists a region \(D\) in the \((y,z)\)-plane and two continuous functions \(x_1(y,z), x_2(y,z)\) such that

    \begin{equation*} E = \{(x,y,z) \in \mathbb{R}^3\ |\ (y,z) \in D, x_1(x,z) \leq x \leq x_2(y,z) \}. \end{equation*}

  3. A region \(E \subset \mathbb{R}^3\) is \(xz\)-supported (also called type 3) if there exists a region \(D\) in the \((x,z)\)-plane and two continuous functions \(y_1(x,z), y_2(x,z)\) such that

    \begin{equation*} E = \{(x,y,z) \in \mathbb{R}^3\ |\ (x,z) \in D, y_1(x,z) \leq y \leq y_2(x,z) \}. \end{equation*}

If the two-dimensional region \(D \subset \mathbb{R}^2\) is also supported on at least one of the two coordinates, we say that the solid region \(E\) is recursively supported. In this case the triple integral can be evaluated as an interated integral.

We note that in the case of rectangular regions, Fubini's theorem still applies, and the order of integration for the iterated integrals does not matter.

Let \(E \subset \mathbb{R}^3\) be the solid region bounded by the planes \(x=0\text{,}\) \(x=2\text{,}\) \(y=2\text{,}\) \(z=0\) and \(z=y\text{.}\) Find the integral of the three-form

\begin{equation*} \omega = x y z\ dx \wedge dy \wedge dz \end{equation*}

over \(E\) with canonical orientation.

By definition, we know that

\begin{equation*} \int_E \omega = \iiint_E x y z\ dV. \end{equation*}

We want to evaluate the triple integral on the right-hand-side.

We can express the region \(E\) as an \(xy\)-supported region. Indeed, if \(D \subset \mathbb{R}^3\) is the rectangular region \(D = [0,2] \times [0,2]\) in the \((x,y)\)-plane, then

\begin{equation*} E = \{(x,y,z) \in \mathbb{R}^3\ |\ (x,y) \in D, 0 \leq z \leq y \}. \end{equation*}

In fact, using the definition of the rectangular region \(D\text{,}\) we could write

\begin{equation*} E = \{(x,y,z) \in \mathbb{R}^3\ |\ x \in [0,2], y \in [0,2], 0 \leq z \leq y \}, \end{equation*}

which shows that \(E\) is recursively supported. We can then write the triple integral as an iterated integral, and evaluate:

\begin{align*} \iiint_E x y z \ dV =\amp \int_0^2 \int_0^2 \int_0^y x y z\ dz dy dx\\ =\amp \int_0^2 \int_0^2 x y \left[ \frac{z^2}{2} \right]_{z=0}^{z=y}\ dy dx\\ =\amp \frac{1}{2} \int_0^2 \int_0^2 x y^3\ dy dx\\ =\amp \frac{1}{2} \int_0^2 x \left[\frac{y^4}{4} \right]_{y=0}^{y=2}\ dx\\ =\amp 2 \int_0^2 x\ dx\\ =\amp 4. \end{align*}

To conclude this section, we should show that our integration theory is invariant under orientation-preserving reparametrizations, just as we did for two-forms in Subsection 5.3.2. We will be brief here and simply state the result. Let \(E_1, E2 \subset \mathbb{R}^3\) be recursively supported regions, and let \(\phi: E_2 \to E_1\) be a bijective and invertible function (that can be extended to a \(C^1\) function on an open subset \(U \subseteq \mathbb{R}^3\) containing \(E_2\)).

We will not write the proof here, as it is almost identical to the proof of the corresponding statement for two-forms in Lemma 5.3.7. The key is that the pullback brings forth the determinant of the Jacobian of the transformation, and invariance reduces to the transformation (or change of variables) formula for triple integrals. As for two-forms, one can say that the transformation formula for triple integrals is simply the statement the integrals of three-forms over regions in \(\mathbb{R}^3\) are invariant under orientation-preserving reparametrizations.

More precisely, just as for two-forms, the transformation formula for triple integrals involves the absolute value of the determinant of the Jacobian, while invariance under pullback for integrals of three-forms involves the determinant of the Jacobian directly. This is because integrals of three-forms are oriented, while triple integrals are not.

Subsection 6.2.2 The divergence theorem in \(\mathbb{R}^3\)

Now that we understand integration of three-forms over regions in \(\mathbb{R}^3\text{,}\) we can go back to the generalized Stokes' theorem Theorem 6.1.1 and see what it becomes when \(M\) is taken to be a solid region \(E \subset \mathbb{R}^3\) that consists of a closed surface and its interior.

We will not prove the divergence theorem here. We note that it follows directly from the generalized Stokes' theorem Theorem 6.1.1, just like our four other integral theorems. The vector calculus translation follows directly from our dictionary between differential forms and vector calculus concepts.

Remark 6.2.7.

Just as for Green's theorem, we can read the divergence theorem in two different ways, starting from the left-hand-side or the right-hand-side. This results in two potential applications: either to evaluate the volume integral of the divergence of a vector field (or an exact three-form), or to evaluate the surface integral of a vector field (a two-form) over a closed surface. However, as was the case for Green's theorem, the divergence theorem is mostly useful to evaluate surface integrals over closed surfaces by transforming them into volume integrals over the interior of the region.

Find the flux of the vector field

\begin{equation*} \mathbf{F}(x,y,z) = (x y, \sin(z^2) + y+ \cos(x^3), e^{x y} ) \end{equation*}

in the outward direction over the surface of the solid region \(E\) that lies above the \((x,y)\)-plane and below the surface \(z=2-x-y^3\text{,}\) \(x \in [-1,1]\text{,}\) \(y \in [-1,1]\text{.}\)

We could try to evaluate the surface integral directly, but given how complicated the vector field is, this would probably be a nightmare. Or we can use the divergence theorem, which tells us that

\begin{equation*} \iint_{\partial E} \mathbf{F} \cdot d \mathbf{S} = \iiint_E (\boldsymbol{\nabla} \cdot \mathbf{F} ) dV. \end{equation*}

The divergence of the vector field is

\begin{equation*} \boldsymbol{\nabla} \cdot \mathbf{F} = y + 1, \end{equation*}

which is of course much simpler, so using the divergence theorem looks like a good strategy.

To evaluate the volume integral we need to write the solid region \(E\) as a recursively supported region. Let us first look at what the solid region looks like. The surface \(Z=2-x-y^3\) is shown below.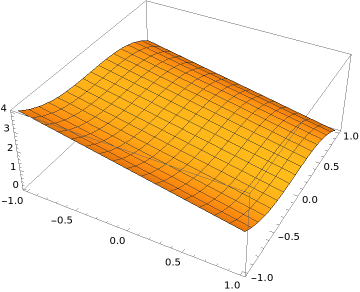

The surface.
Figure 6.2.9. The surface \(z=2-x-y^3\) over the rectangle \([-1,1] \times [-1,1]\) in the \((x,y)\)-plane.

The solid region \(E\) consists of the region bounded by the surface shown above, the four sides of the box in the figure, and the bottom of the box. It can be written as an \(xy\)-supported region:

\begin{equation*} E = \{ (x,y,z) \in \mathbb{R}^3\ | \ x\in[-1,1], y\in[-1,1], 0 \leq z \leq 2 -x - y^3 \}. \end{equation*}

The volume integral can then be evaluated:

\begin{align*} \iiint_E (\boldsymbol{\nabla} \cdot \mathbf{F} ) dV=\amp \int_{-1}^1 \int_{-1}^1 \int_0^{2-x-y^3} (y+1)\ dz dy dx\\ =\amp \int_{-1}^1 \int_{-1}^1 (y+1) \left[ z \right]_{z=0}^{z=2-x-y^3}\ dy dx\\ =\amp \int_{-1}^1 \int_{-1}^1 (2 y - x y - y^4 + 2 - x -y^3)\ dy dx\\ =\amp \int_{-1}^1 \left[y^2 - \frac{x y^2}{2} - \frac{y^5}{5} + 2 y - x y - \frac{y^4}{4} \right]_{y=-1}^{y=1}\ dx\\ =\amp \int_{-1}^1 \left(\frac{18}{5} - 2 x \right)\ dx\\ =\amp \frac{36}{5}. \end{align*}

Therefore, by the divergence theorem, the flux of \(\mathbf{F}\) over the surface \(\partial E\) is equal to \(36/5\text{.}\)

Exercises 6.2.3 Exercises

1.

Use the divergence theorem to find the surface integral of the two-form

\begin{equation*} \omega = 3 x y^2\ dy \wedge dz + (e^x z + y z^2)\ dz \wedge dx + x y\ dx \wedge dy \end{equation*}

over the surface of the solid bounded by the cylinder \(y^2+z^2=1\) and the planes \(x=-1\text{,}\) \(x=-2\text{,}\) with orientation given by an outward pointing normal vector.

Solution.

Let \(E\) be the solid region described in the problem, and \(\partial E\) its boundary surface with outward pointing normal vector. The divergence theorem tells us that

\begin{equation*} \int_{\partial E} \omega = \int_E d \omega, \end{equation*}

where the integral on the right-hand-side is over the solid region \(E\) with canonical orientation. Thus instead of evaluating the surface integral, we can evaluate the volume integral of the three-form \(d \omega\) over the solid region \(E\text{.}\)

We calculate the exterior derivative:

\begin{equation*} d \omega = (3 y^2 + z^2)\ dx \wedge dy \wedge dz. \end{equation*}

To evaluate the integral of \(d \omega\) over \(E\text{,}\) we describe the solid region \(E\) as a recursively supported region. In fact, it is easiest to work in cylindrical coordinates (to be clear, you could do the whole calculation in Cartesian coordinates as well, and you would get the same answer, but I find it easier to work with cylindrical coordinates). So we do the change of coordinates \(\phi: E' \to E\) with

\begin{equation*} \phi(u, r, \theta) = (u, r \cos(\theta), r \sin(\theta) ). \end{equation*}

The pullback of \(d \omega\) is easily calculated to be:

\begin{align*} \phi^*(d \omega) =\amp (3 r^2 \cos^2(\theta) + r^2 \sin^2(\theta) ) r\ du \wedge dr \wedge d\theta \\ =\amp r^3(1 + 2 \cos^2(\theta) )\ du \wedge dr \wedge d\theta. \end{align*}

We note that the determinant of the Jacobian is \(r\text{,}\) which is positive, and hence the integral is invariant under the change of coordinates (pullback). Thus we can rewrite the integral as

\begin{align*} \int_E d \omega =\amp \int_{E'} \phi^*(d \omega) \\ =\amp \int_{E'} r^3 (1+2 \cos^2(\theta))\ du \wedge dr \wedge d\theta. \end{align*}

The region \(E'\) is easily described as a rectangular region in \((u,r,\theta)\text{:}\)

\begin{equation*} E' = \{(u,r,\theta) \in \mathbb{R}^3\ |\ u \in [-2,-1], r \in [0,1], \theta \in [0, 2 \pi] \}. \end{equation*}

The volume integral can finally be evaluated:

\begin{align*} \int_{E'} r^3 (1+2 \cos^2(\theta))\ du \wedge dr \wedge d\theta =\amp \int_{-2}^{-1} \int_0^1 \int_0^{2 \pi} r^3 (1+2 \cos^2(\theta)) d \theta dr du\\ =\amp 4 \pi \int_{-2}^{-1} \int_0^1 r^3\ dr du\\ =\amp \pi \int_{-2}^{-1} du\\ =\amp \pi. \end{align*}

Therefore, the integral of \(\omega\) over the surface \(\partial E\) specified in the question is equal to \(\pi\text{.}\)

2.

Use the divergence theorem to find the flux of the vector field

\begin{equation*} \mathbf{F}(x,y,z) = (z + \sin(y), y, e^x ) \end{equation*}

across (in the outward direction) the sphere \(x^2+y^2+z^2 = 16\text{.}\)

Solution.

Let \(E\) be the sphere and its interior, and \(\partial E\) be the sphere with outward pointing normal vector. The divergence theorem tells us that

\begin{equation*} \iint_{\partial E} \mathbf{F} \cdot d \mathbf{S} = \iiint_E \boldsymbol{\nabla} \cdot \mathbf{F}\ dV, \end{equation*}

where the integral on the right-hand-side is with canonical orientation.

We first calculate the divergence of \(\mathbf{F}\text{:}\)

\begin{equation*} \boldsymbol{\nabla} \cdot \mathbf{F} = 0 + 1 + 0 = 1. \end{equation*}

Thus the integral that we are interested in is

\begin{equation*} \iiint_E \boldsymbol{\nabla} \cdot \mathbf{F}\ dV = \iiint_E\ dV, \end{equation*}

which is simply the volume of the solid region \(E\text{.}\) As \(E\) is the interior of the sphere of radius \(4\text{,}\) we know right away that its volume is

\begin{equation*} \frac{4}{3} \pi (4^3) = \frac{256\pi}{3}, \end{equation*}

so we could conclude right away that the flux of the vector field across the sphere \(\partial E\) is equal to \(\frac{256\pi}{3}\text{.}\)

3.

Use the divergence theorem to evaluate the surface integral of the two-form

\begin{equation*} \omega = (3 x^3 + y z)\ dy \wedge dz + (y^3 + x z)\ dz \wedge dx + (3 z y^2 + x^7)\ dx \wedge dy \end{equation*}

over the surface of the solid bounded by the paraboloid \(z = 1-x^2-y^2\) and the \((x,y)\)-plane, with orientation given by an inward pointing normal vector.

Solution.

First, we note that the problem is asking to evaluate the surface integral with a normal vector pointing inward. Thus, if we denote the solid region by \(E\) and its boundary surface by \(\partial E\) the divergence theorem tells us that

\begin{equation*} \int_{\partial E_-} \omega= - \int_{E} d \omega, \end{equation*}

where on the left-hand-side we mean the surface integral with normal vector pointing inward, while on the right-hand-side we mean the volume integral with canonical orientation.

We calculate the exterior derivative:

\begin{equation*} d \omega = (9 x^2 + 3 y^2 + 3 y^2)\ dx \wedge dy \wedge dz = 3 (3 x^2 + 2 y^2)\ dx \wedge dy \wedge dz. \end{equation*}

We can either work in Cartesian or cylindrical coordinates here. But cylindrical coordinates will make the calculation much easier (believe me: I first did it in Cartesian coordinates, and it is no fun! See below. :-). So we do the change of coordinates \(\phi: E' \to E\) with

\begin{equation*} \phi(r, \theta,u) = (r \cos(\theta), r \sin(\theta), u). \end{equation*}

The pullback of \(d \omega\) is easily calculated to be:

\begin{align*} \phi^*(d \omega) =\amp 3 (3 r^2 \cos^2(\theta) + 2 r^2 \sin^2(\theta) ) r\ dr \wedge d\theta \wedge du.\\ =\amp 3 r^3(2 + \cos^2(\theta) )\ dr \wedge d\theta \wedge du. \end{align*}

We note that the determinant of the Jacobian is \(r\text{,}\) which is positive, and hence the integral is invariant under the change of coordinates (pullback). Thus we can rewrite the integral as

\begin{align*} \int_E d \omega =\amp \int_{E'} \phi^*(d \omega) \\ =\amp \int_{E'} 3 r^3 (2+ \cos^2(\theta))\ dr \wedge d\theta \wedge du. \end{align*}

The region \(E'\) is easily described as a recursively supported region in \((r,\theta,u)\text{:}\)

\begin{equation*} E' = \{(r,\theta,u) \in \mathbb{R}^3\ |\ r \in [0,1], \theta \in [0, 2 \pi], 0 \leq u \leq 1-r^2 \}. \end{equation*}

The volume integral becomes

\begin{align*} \int_{E'} \phi^*(d \omega)=\amp 3 \int_0^1 \int_0^{2 \pi} \int_0^{1-r^2} r^3(2+\cos^2(\theta))\ du d\theta dr\\ =\amp 3 \int_0^1 \int_0^{2\pi} r^3(2+\cos^2(\theta)) (1-r^2)\ d\theta dr\\ =\amp 15 \pi \int_0^1 (r^3-r^5)\ dr\\ =\amp 15 \pi \left( \frac{1}{4} - \frac{1}{6} \right)\\ =\amp \frac{5 \pi}{4}. \end{align*}

Therefore, by the divergence theorem the surface integral of the two-form that we are asked to evaluate is equal to minus this result (the surface integral is with respect to a normal vector pointing inward, as mentioned above), and thus is equal to \(-\frac{5 \pi}{4}\text{.}\)

For completeness, let me do the calculation in Cartesian coordinates as well -- you will see how much uglier it is. The solid is given by the region enclosed by the parabola \(z=1-x^2-y^2\) above the disk \(x^2+y^2=1\) in the \((x,y)\)-plane. We describe the solid region as a recursively supported region:

\begin{equation*} E = \{(x,y,z) \in \mathbb{R}^3\ |\ x \in [-1,1], - \sqrt{1-x^2} \leq y \leq \sqrt{1-x^2}, 0 \leq z \leq 1 - x^2 - y^2 \}. \end{equation*}

The volume integral becomes:

\begin{align*} \int_E d \omega =\amp 3 \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \int_0^{1-x^2-y^2} (3x^2+2 y^2)\ dz dy dx\\ =\amp 3 \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} (3 x^2+2 y^2) (1-x^2-y^2)\ dy dx\\ =\amp 3 \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} (3 x^2 - 3 x^4 +(- 5 x^2 + 2) y^2- 2 y^4)\ dy dx\\ =\amp 3 \int_{-1}^1 \left[y ( 3x^2- 3x^4 +\frac{1}{3}(-5 x^2+2) y^2 - \frac{2}{5} y^4) \right]_{y=-\sqrt{1-x^2}}^{y=\sqrt{1-x^2}}\ dx\\ =\amp 6 \int_{-1}^1 \sqrt{1-x^2} \left( 3 x^2 - 3 x^4 +\frac{1}{3}(-5 x^2+2)(1-x^2) - \frac{2}{5}(1-x^2)^2 \right)\ dx\\ =\amp 6 \int_{-1}^1 \sqrt{1-x^2} \left(- \frac{26}{15} x^4 + \frac{22}{15} x^2 + \frac{4}{15} \right)\ dx\\ =\amp 6 \int_{-\pi/2}^{\pi/2} \cos^2(\theta) \left(- \frac{26}{15} \sin^4(\theta) + \frac{22}{15} \sin^2(\theta) + \frac{4}{15} \right) d\theta\\ =\amp \frac{5 \pi}{4}. \end{align*}

Here I used the trigonometric substitution \(x = \sin(\theta)\text{,}\) and to evaluate the last trigonometric integral one needs to use a whole bunch of trigonometric identities (or a computer algebra system :-). We fortunately get the same result as before for the volume integral, and we conclude as before that the surface integral is equal to minus this result, that is, \(- \frac{5 \pi}{4}\text{.}\)

4.

Show that the volume \(V\) of a solid region \(E \subset \mathbb{R}^3\) bounded by a closed surface \(\partial E\) can be written as

\begin{equation*} V = \int_{\partial E}\ x\ dy \wedge dz, \end{equation*}

where the surface integral is evaluated with the orientation given by an outward pointing normal vector.

Solution.

We know that the volume of the region \(E\) is given by the integral of the basic three-form \(\omega = dx \wedge dy \wedge dz\) over \(E\) with canonical orientation:

\begin{equation*} V = \int_E dx \wedge dy \wedge dz. \end{equation*}

But \(\omega = dx \wedge dy \wedge dz\) is exact, as it can be written as \(\omega = d \eta\) for the two-form \(\eta = x \ dy \wedge dz\text{.}\) Therefore, by the divergence the theorem, we know that

\begin{equation*} \int_E dx \wedge dy \wedge dz = \int_{\partial E} x\ dy \wedge dz, \end{equation*}

where the integral on the right-hand-side is the surface integral with orientation given by an upward pointing normal vector.

5.

We studied the two-form

\begin{equation*} \omega = \frac{1}{(x^2+y^2+z^2)^{3/2} } (x\ dy \wedge dz + y \ dz \wedge dx + z\ dx \wedge dy) \end{equation*}

in Remark 4.6.6 and Exercise 5.8.3.5. \(\omega\) is defined on \(U = \mathbb{R}^3 \setminus \{ (0,0,0) \}\text{.}\) We proved in Exercise 5.8.3.5 that \(\omega\) is closed, but that it is not exact, by showing that its surface integral along the sphere \(x^2+y^2+z^2=1\) is equal to \(4 \pi\text{.}\) In this problem we show that the surface integral of \(\omega\) is non-vanishing for all closed surface that contain the origin (and always equal to \(4 \pi\)), while it vanishes for all closed surfaces that do not pass through or enclose the origin.

  1. Consider an arbitrary closed surface \(S_0\) with outward pointing normal vector that does not contain or pass through the origin. Use the divergence theorem to show that

    \begin{equation*} \int_{S_0} \omega = 0. \end{equation*}

  2. Let \(S_1\) be an arbitrary closed surface with outward pointing normal vector that contains the origin. Explain why the argument of (a) does not apply here.

  3. Let \(S_1\) be an arbitrary closed surface with outward pointing normal vector that contains the origin. Let \(K\) be a sphere centered at the origin, with a radius small enough that it is contained completely inside \(S_1\text{.}\) Give \(K\) the orientation of a normal vector pointing outward (outward of the sphere \(K\)). Use the divergence theorem to show that

    \begin{equation*} \int_{S_1} \omega = \int_K \omega. \end{equation*}

  4. Using part (c), show that it implies that

    \begin{equation*} \int_{S_1} \omega = 4 \pi. \end{equation*}

You have shown that the surface integral of \(\omega\) along any closed surface that contains the origin is \(4 \pi\text{,}\) while the surface integral of \(\omega\) along any closed surface that does not enclose or pass through the origin is zero. Note that this is the argument that is needed to show that, using Gauss's law, the total charge contained within any closed surface that encloses a point charge \(q\) at the origin is always equal to \(q\) -- see Example 5.9.2.

Solution.

(a) We know that the two-form \(\omega\) is closed, that is, \(d \omega = 0\text{.}\) Furthermore, \(\omega\) is defined on \(U=\mathbb{R}^3 \setminus \{(0,0,0) \}\text{.}\) If the surface \(S_0\) does not contain or pass through the origin, then the surface \(S_0\) and the solid region \(E_0\) bounded by \(S_0\) lie within \(U\text{,}\) the domain of definition of \(\omega\text{.}\) Therefore, by the divergence theorem,

\begin{equation*} \int_{S_0} \omega = \int_{E_0} d \omega = 0. \end{equation*}

(b) If \(S_1\) contains the origin in its interior, we cannot apply the divergence theorem as in (a), since the solid region \(E_1\) bounded by \(S_1\) does not lie within \(U\text{,}\) the domain of definition of \(\omega\text{.}\)

(c) We stated the divergence theorem only for solid regions that consisted of a single closed surface and its interior, but it in fact applies to any closed bounded region. One simply needs to make sure that each bounding surface is oriented with an outward pointing normal vector, where “outward” means away from the solid region bounded by the surfaces.

In particular, we can consider the solid region \(E\) that is inside \(S_1\text{,}\) but outside the sphere \(K\text{.}\) It is bounded by the two closed surfaces \(S_1\) and \(K\text{.}\) As the origin is inside \(K\text{,}\) it is not within the solid region \(E\text{.}\) Therefore, \(E \subset U\text{,}\) and the divergence theorem applies to this solid region. In this case, the divergence theorem says that the sum of the surface integral over the outer boundary \(S_1\) with outward pointing normal vector and the inner boundary \(K\) with vector pointing away from the solid region (which means that it is pointing inside the sphere \(K\)) is equal to the volume integral over \(E\text{,}\) which is zero since \(d \omega = 0\text{:}\)

\begin{equation*} \int_{S_1,\text{out}} \omega + \int_{K,\text{in}} \omega = \int_E d \omega = 0. \end{equation*}

We conclude that

\begin{equation*} \int_{S_1,\text{out}} \omega = - \int_{K,\text{in}} \omega. \end{equation*}

To get rid of the minus sign, we can reverse the orientation on \(K\text{,}\) and consider a normal vector that points outward of the sphere \(K\text{.}\) We get:

\begin{equation*} \int_{S_1,\text{out}} \omega = \int_{K,\text{out}} \omega, \end{equation*}

as stated in the question.

(d) We already calculated the surface integral of \(\omega\) along the sphere \(x^2+y^2+z^2=1\) in Exercise 5.8.3.5 and obtained the result \(4 \pi\text{.}\) In fact, the same calculation for a sphere of arbitrary radius \(x^2+y^2+z^2 = R^2\) would still give \(4 \pi\) (in fact we already did this calculation in Exercise 5.6.4.5). Therefore, by (c), we conclude that the surface integral of \(\omega\) along an arbitrary closed surface \(S_1\) that contains the origin, with outward pointing normal vector, is:

\begin{equation*} \int_{S_1} \omega = 4 \pi. \end{equation*}