Bremsstrahlung

When electrons scatter they can emit real photons. This process is called bremsstrahlung because it involves an acceleration or deceleration (in German ``bremson'') of the projectile. This bremsstrahlung or deceleration radiation with the emission of a single photon is a well-defined process only within certain limits: the simultaneous emission of very soft photons - too soft to be observed within the accuracy of the energy determination of the incident and outgoing electron - can never be excluded. In fact, this radiation is always present, even in so-called elastic scattering. Therefore, it will be impossible to make a clean physical distinction between bremsstrahlung and radiationless scattering when the emitted photon is very soft. We shall restrict ourselves, therefore to the emission of one not-too-soft photon.

Consider the emission of radiation of a charged particle (electron) in the presence of an external field. The four-vector potential of a photon with momentum $k_\mu=(\omega,\vec{k})$ and polarization $\varepsilon^\mu(\vec{k},\lambda)$ is written in Heaviside-Lorentz system of units as the plane wave

$$A^\mu(x;k) = \frac{\varepsilon^\mu(\vec{k},\lambda)}{\sqrt{2\omega V}} (e^{-ik\cdot x} + e^{ik\cdot x}) .$$ (7.180)

For simplicity we return to the static approximation and replace the photon by a static Coulomb field and calcualte $S_{fi}$ to lowest non-vanishing order in $e$. There can be no first-order emission of radiation by a free electron in the absence of the external filled. This is kinematically forbidden, since it is impossible to conserve energy and momentum: $k^2=0\neq(p_i-p_f)^2<0$.

The Feynman diagrams (figure 7.5) for this process correspond to a second-order process with one vertex for the interaction of the electron with the Coulomb field and one for the emission of the bremsstrahlung quantum.

Figure 7.5: Feynman diagrams for bremsstrahlung production in a Coulomb field.

The second-order $S$-matrix element is

$$S_{fi} = e^2 \int d^4x d^4y \overline{\psi}_f(x) [ -i\not{\!\!A}(x;k) iS_F(x-y) (-i\gamma^0) A_0^\mathrm{coul}(y)$$

$$+ (-i\gamma^0)A_0^\mathrm{coul}(x) iS_F(x-y) ( -i\not{\!\!A}(y;k))]\psi_i(y) ,$$ (7.181)

where $A_0^\mathrm{coul}=\frac{-Ze}{4\pi\vert\vec{x}\vert}$, and the two terms correspond to the two orderings of the vertices.

It is convenient to transform to momentum space by Fourier-expanding all factors and carrying out the coordinate integrations.

$$S_{fi} = e^2 \int d^4x d^4y \sqrt{\frac{m}{E_fV}} \overline{u}(p_f,s_f) e^... ...t x}) \int \frac{d^4q}{(2\pi)^4} e^{-iq\cdot (x-y)} \frac{i}{\not{q}-m} \right.$$

$$\times \left. (-i\gamma_0) \left( \frac{-Ze}{4\pi\vert\vec{y}\vert} \rig... ...-i\not{\varepsilon}}{\sqrt{2\omega V}} (e^{-ik\cdot y} + e^{ik\cdot y}) \right]$$

$$\times \sqrt{\frac{m}{E_iV}} u(p_i,s_i) e^{-ip_i\cdot y}$$

$$= \frac{-Ze^3}{4\pi} \int \frac{d^4xd^4yd^4q}{(2\pi)^4V^{3/2}} \sqr... ... \frac{1}{\vert\vec{y}\vert} e^{ix\cdot(p_f\mp k-q)} e^{iy\cdot(q-p_i)} \right.$$

$$+ \left. (-i\gamma_0) \frac{1}{\vert\vec{x}\vert} \frac{i}{\not{q}-... ...not{\varepsilon}) e^{ix\cdot(p_f-q)} e^{iy\cdot(q\mp k-p_i)} \right] u(p_i,s_i)$$

$$= \frac{-Ze^3}{4\pi} \int \frac{d^4q}{V^{3/2}} \sqrt{\frac{m^2}{2\o... ...int\frac{d^4y}{\vert\vec{y}\vert} \delta(p_f\mp k-q) e^{iy\cdot(q-p_i)} \right.$$

$$+ \left. (-i\gamma_0) \int \frac{d^4x}{\vert\vec{x}\vert} \frac{i}{... ...-i\not{\varepsilon}) e^{ix\cdot(p_f-q)} \delta^4(q\mp k-p_i) \right] u(p_i,s_i)$$

$$= \frac{-Ze^3}{4\pi} \frac{1}{V^{3/2}} \sqrt{\frac{m^2}{2\omega E_i... ...i\gamma_0) \int\frac{d^4y}{\vert\vec{y}\vert} e^{iy\cdot(p_f\mp k-p_i)} \right.$$

$$+ \left. (-i\gamma_0) \int \frac{d^4x}{\vert\vec{x}\vert} \frac{i}{... ...pm\not{k}-m} (-i\not{\varepsilon}) e^{ix\cdot(p_f-p_i\mp k)} \right] u(p_i,s_i)$$

$$= \frac{-Ze^3}{V^{3/2}} 2\pi \delta(E_f+k-E_i) \frac{1}{\sqrt{2\ome... ...varepsilon}) \frac{i}{\not{\;\!\!\!p}_f+\not{\;\!\!\!k}-m} (-i\gamma_0) \right.$$

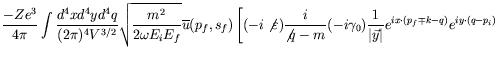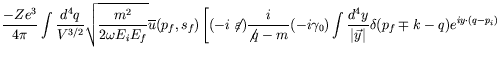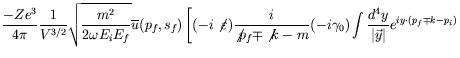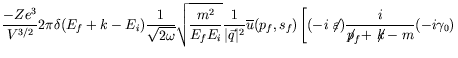$$+ \left. (-i\gamma_0) \frac{i}{\not{\;\!\!\!p}_f-\not{\;\!\!\!k}-m} (-i\not{\;\!\!\!\varepsilon}) \right] u(p_i,s_i) ,$$ (7.182)

where $q=p_f+k-p_i$ and we have taken the $E_f+k-E_i$ solution only. There is an additional contribution coming from the first term of the photon potential for which the energy $\delta$-function is $\delta(E_i+k-E_f)$. This term describes absorption of energy in the scattering process and does not contribute to the process of interest here, in which the incident electron gives up energy to the radiation field and emerges with $E_f=E_i-k<E_i$.

We notice the factor $(-i\not{\;\!\!\!\varepsilon})$ appears at the vertex where a free photon of polarization $\varepsilon_\mu$ is emitted, and $1/\sqrt{2\omega V}$ appears as the normalization factor for a photon wave function

We limit our derivation to $k\rightarrow 0$, or to the emission of a very soft photon. The more general result is known as the Bethe-Heitler formula. In the limit of $k\rightarrow 0$ the factor within brackets can be approximated as

$${\mathcal{M}}_\mu(k) \equiv -i\overline{u}(p_f,s_f)\left[ \gamma_\mu \frac{\not{\;\!\!\!p}_f+... ...mma_0 \frac{\not{\;\!\!\!p}_i-k+m}{(p_i-k)^2-m^2} \gamma_\mu \right] u(p_i,s_i)$$

$$\varepsilon^\mu{\mathcal{M}}_\mu(k) \approx -i\overline{u}(p_f,s_f)\left[ \frac{2\varepsilon\cdot p_f - (\not... ...not{\;\!\!\!\varepsilon}(\not{\;\!\!\!p}_i-m)}{-2k\cdot p_i} \right] u(p_i,s_i)$$

$$= -i\overline{u}(p_f,s_f) \gamma_0 u(p_i,s_i) \left( \frac{\varepsilon\cdot p_f}{k\cdot p_f} - \frac{\varepsilon\cdot p_i}{k\cdot p_i} \right).$$ (7.183)

Proceeding to the cross-section, we square $S_{fi}$, divide by the flux $\vert\vec{v}\vert/V=p_i/(E_iV)$ and by $2\pi\delta(0)$ to form a rate, and sum over final states $(V^2d^3kd^3p_f)/(2\pi)^6$ in the observed interval of phase space. We obtain

$$d\sigma = \int \frac{Vd^3k}{(2\pi)^3} \frac{Vd^3p_f}{(2\pi)^3} \frac{VE_i}{p_i} \frac{\vert S_{fi}\vert^2}{2\pi\delta(0)}$$

$$= \int \frac{V^3}{(2\pi)^6} \frac{d^3kd^3p_f}{p_i/E_i} \frac{Z^2e^6... ...ega} \frac{m^2}{E_fE_i} \frac{1}{\vert\vec{q}\vert^4} \vert{\mathcal{M}}\vert^2$$

$$= \int \frac{Z^2(4\pi\alpha)^2e^2}{(2\pi)^6} d^3k d^3p_f (2\pi) \de... ...omega} \frac{m^2}{p_iE_f} \frac{1}{\vert\vec{q}\vert^4} \vert\mathcal{M}\vert^2$$

$$= \int \frac{4Z^2\alpha^2m^2}{\vert\vec{q}\vert^4} \frac{e^2}{(2\pi... ..._f \delta(E_f+k-E_i) \frac{1}{2\omega} \frac{\vert\mathcal{M}\vert^2}{p_iE_f} .$$ (7.184)

Identifying terms with the elastic scattering cross-section (equation 7.44) we find

$$d\sigma = \left( \frac{d\sigma}{d\Omega} \right)_{elastic} \frac{e^2}{(2\pi... ...silon\cdot p_f}{k\cdot p_f} - \frac{\varepsilon\cdot p_i}{k\cdot p_i} \right)^2$$

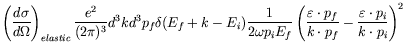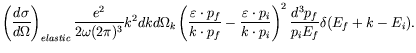$$= \left( \frac{d\sigma}{d\Omega} \right)_{elastic} \frac{e^2}{2\ome... ...silon\cdot p_i}{k\cdot p_i} \right)^2 \frac{d^3p_f}{p_iE_f} \delta(E_f+k-E_i) .$$ (7.185)

Using

$$d^3p_f = p_f^2dp_fd\Omega_f = p_fE_fdE_fd\Omega_f$$ (7.186)

we have

$$\frac{d\sigma}{d\Omega_f} = \left( \frac{d\sigma}{d\Omega} \... ...k\cdot p_i} \right)^2 \frac{p_f}{p_i} dE_f \delta(E_f+k-E_i) .$$ (7.187)

Since $k\rightarrow 0$, we can take $p_f/p_i\rightarrow 1$. Using

$$\int_m^\infty dE_f \delta(E_f+k-E_i) = \int_{-\infty}^\infty dE_f \delta(E_f+k-E_i) \theta(E_f-m) = \theta(E_i-k-m) ,$$ (7.188)

we have

$$\frac{d\sigma}{d\Omega_f} = \left(\frac{d\sigma}{d\Omega_f}\... ...{\varepsilon\cdot p_i}{k\cdot p_i} \right)^2 \theta(E_i-m-k).$$ (7.189)

This is the cross-section for the electron to be observed in a solid angle $d\Omega_f$ and for a photon of polarization $\varepsilon$ to emerge with $\vec{k}$ in the interval $d\Omega_kdk$.

The result is more general than one might expect. It has been shown that in the limit $k\rightarrow 0$ the amplitude for any process leading to photon emission can be factorized according to

$$\lim_{k\rightarrow 0} M(k) = \sqrt{\alpha} \left( \frac{\var... ... p_f} - \frac{\varepsilon\cdot p_i}{k\cdot p_i} \right) M_0 ,$$ (7.190)

where $M_0$ is the amplitude for the same process without photon emission. This result is true for any kind of process, irrespective of the spin or internal structure of the charged particle.

We notice that the photon energy spectrum behaves as $dk/k$ and therefore for the probability to emit a zero-energy photon is infinite. This is the ``infrared catastrophe''. For a consistent comparison with experiment we must include both elastic and inelastic cross-sections calculated to the same order in $e^2$. Since the bremsstrahlung contribution is of order $e^2$ relative to the elastic scattering, we must also include radiative corrections to $(d\sigma/d\Omega_f)_{elastic}$ to the same order $e^2$. These correspond to second-order scattering of the electron in the Coulomb field plus we must take into account the interaction of the electron with itself via the radiation field (figure 7.6). The amplitude coming from these later processes contain a divergent term which precisely cancels the divergence at $k=0$.

Figure 7.6: Radiative corrections to Coulomb scattering.

Before evaluating the matrix element, we look at how gauge invariance of the electromagnetic field puts a condition on the electromagnetic current in momentum space. The interaction of any electromagnetic current, $J_\mu(x)$, with the vector potential, $A_\mu(x)$, is given by

$$\int d^4x J_\mu(x) A^\mu(x) .$$ (7.191)

The integral must be invariant under the gauge transformation

$$A^\mu(x) \rightarrow A^\mu(x) + \frac{\partial\Lambda(x)}{\partial x_\mu} .$$ (7.192)

Integrating by parts this implies

$$\int d^4x J_\mu(x)\frac{\partial\Lambda(x)}{\partial x_\mu} ... ...d^4x \frac{\partial J_\mu(x)}{\partial x_\mu} \Lambda(x) = 0 .$$ (7.193)

Since $\Lambda(x)$ is an arbitrary function this yields the condition of current conservation

$$\frac{\partial J_\mu(x)}{\partial x_\mu} = 0 ,$$ (7.194)

which can be written in momentum space as

$$k_\mu J^\mu(k) = 0 .$$ (7.195)

This property is shared also by quantum mechanical transitions currents. Thus we can expect that the matrix element $\mathcal{M}_\mu(k)$ satisfies

$$k^\mu \mathcal{M}_\mu(k) = 0 ,$$ (7.196)

since $\mathcal{M}$ is the transition current for bremsstrahlung up to a numerical factor. Using the matrix element in equation 7.183 this condition is easily shown to be true.

We now turn to the evaluation of the summation over the photon polarizations. The quantity of interest is

$$\overline{\vert\varepsilon\cdot\mathcal{M}\vert^2} = \sum_{\lambda=1,2} \vert\varepsilon_\mu(\vec{k},\lambda) \mathcal{M}^\mu(k)\vert^2$$

$$= \sum_{\lambda=1,2} \varepsilon_\mu(\vec{k},\lambda) \varepsilon_\nu^*(\vec{k},\lambda) \mathcal{M}^\mu(k) \mathcal{M}^{*\nu}(k).$$ (7.197)

Since this is a scalar, we can evaluate it in an arbitrary Lorentz frame. Orienting the coordinates such that $k^\mu=\omega(1,0,0,1)$, where $\omega=\vert\vec{k}\vert$, since $k^2=0$. We choose $A^0(x)=0$. In this system $\vec{A}(x)$ is transverse and the two independent transverse polarizations may be written as

$$\varepsilon(\vec{k},1) = (0,1,0,0)$$ (7.198)

$$\varepsilon(\vec{k},2) = (0,0,1,0) .$$ (7.199)

Therefore $\varepsilon(\vec{k},1)\cdot k=0$ and $\varepsilon(\vec{k},2)\cdot k=0$, $\varepsilon(\vec{k},1)\cdot\varepsilon(\vec{k},2)=0$ and $\varepsilon(\vec{k},1)\cdot \varepsilon(\vec{k},1) =\varepsilon(\vec{k},2)\cdot\varepsilon(\vec{k},2)=-1$.

Summing over polarizations we have

$$\overline{\vert\varepsilon\cdot\mathcal{M}\vert^2} = \mathcal{M}^1\mathcal{M}^{*1} + \mathcal{M}^2\mathcal{M}^{*2} .$$ (7.200)

Invoking our condition of current conservation, we have

$$k_\mu\mathcal{M}^\mu = \omega(\mathcal{M}^0 - \mathcal{M}^3) = 0 ,$$ (7.201)

which implies $\mathcal{M}^0 = \mathcal{M}^3$. Then we transform into a four dimensional scalar product by adding the vanishing contributions

$$\overline{\vert\varepsilon\cdot\mathcal{M}\vert^2} = \mathca... ...M}^0\mathcal{M}^{*0} = - \mathcal{M}_\mu\mathcal{M}^{*\mu} .$$ (7.202)

Since this result is covariant, we compare it with equation 7.197 to write

$$\sum_{\lambda=1,2} \varepsilon_\mu(\vec{k},\lambda)\varepsilon_\nu(\vec{k},\lambda) = -g_{\mu\nu} + \mathrm{gauge\ terms} .$$ (7.203)

The additional gauge terms need not be specified in detail. They are proportional to $k_\mu$ and $k_\nu$ and thus do not contribute to any observable quantity since our result will be multiplied with conserved currents which satisfy $k\cdot J=0$. Nevertheless these terms have to be present since a complete basis in 4-dimension space of Lorentz vectors has to contain 4 elements. The contribution of longitudinal $\varepsilon_\mu(\vec{k},3)$ and scalar $\varepsilon_\mu(\vec{k},0)$ photons to the completeness relation makes their appearance on the right-hand side of our result. They do not correspond to physical photons however. We have thus proven the completeness relation of the polarization vectors.

We now apply this completeness relation to the bremsstrahlung cross-section. Notice

$$\sum_{\lambda=1,2} \left( \frac{\varepsilon\cdot p_f}{k\cdot... ...cdot p_i)^2} +\frac{2p_f\cdot p_i}{(k\cdot p_f)(k\cdot p_i)}$$ (7.204)

and thus

$$\frac{d\sigma}{d\Omega_f} = \left( \frac{d\sigma}{d\Omega_f} \right)_{elastic} \frac{4\pi\alpha}{2(2\pi)^3} \int kdk \int d\Omega_k$$

$$\cdot \left[ \frac{2p_f\cdot p_i}{(k\cdot p_f)(k\cdot p_i)} -\frac{m^2}{(k\cdot p_f)^2} -\frac{m^2}{(k\cdot p_i)^2} \right] \theta(E_i-m-k) .$$ (7.205)

Integrating over all photons emission angles and energies in the interval $0<k_{min}\le k\le k_{max}\ll E_i$ gives

$$\frac{d\sigma}{d\Omega_f} = \left( \frac{d\sigma}{d\Omega_f}... ...ac{m^2}{(k\cdot p_f)^2} -\frac{m^2}{(k\cdot p_i)^2} \right] .$$ (7.206)

Writing $k\cdot p_f = kE_f - \vec{k}\cdot\vec{p}_f = k(E_f - \hat{k}\cdot\vec{p}_f) = kE_f(1 -\hat{k}\cdot\vec{\beta}_f)$ we have

$$\frac{d\sigma}{d\Omega_f} = \left( \frac{d\sigma}{d\Omega_f} \right)_{elastic} \frac{\alpha}{... ...\beta}_i)} {(1-\hat{k}\cdot\vec{\beta}_f)(1-\hat{k}\cdot\vec{\beta}_i)} \right.$$

$$\left. -\frac{m^2}{E_f^2(1-\hat{k}\cdot\vec{\beta}_f)^2} -\frac{m^2}{E_i^2(1-\hat{k}\cdot\vec{\beta}_i)^2} \right].$$ (7.207)

To integrate the last two terms in equation 7.207 we use

$$\int\frac{d\Omega_f}{4\pi} \frac{m^2}{E^2(1-\vec{\beta}\cdot\hat{k})^2} = \frac{m^2}{2E^2} \int_0^1 d\cos\theta \frac{1}{(1-\beta\cos\theta)^2}$$

$$= \frac{1-\beta^2}{2} \left[ \frac{1}{\beta(1-\beta)} - \frac{1}{\beta(1+\beta)} \right]$$

$$= 1.$$ (7.208)

To evaluate the first integral we use

$$\frac{1}{ab} = \int_0^1 \frac{dx}{[ax+b(1-x)]^2}$$ (7.209)

to obtain

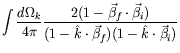$$\int\frac{d\Omega_k}{4\pi}\frac{2(1-\vec{\beta}_f\cdot\vec{\beta}_i)} {(1-\hat{k}\cdot\vec{\beta}_f)(1-\hat{k}\cdot\vec{\beta}_i)} = \int_0^1 dx \int\frac{d\Omega_f}{4\pi} \frac{2(1-\vec{\beta}_f\cd... ...}_i)} {[(1-\hat{k}\cdot\vec{\beta}_f)x + (1-\vec{k}\cdot\vec{\beta}_i)(1-x)]^2}$$

$$= \int_0^1 dx\int\frac{d\Omega_f}{4\pi} \frac{2(1-\vec{\beta}_f\cdot\vec{\beta}_i)}{[1-\hat{k}\cdot(\vec{\beta}_fx + \vec{\beta}_i(1-x))]^2} .$$ (7.210)

Using

$$\int \frac{dx}{(a+bx)^2} = -\frac{1}{b(a+bx)}$$ (7.211)

we have

$$\int\frac{d\Omega_k}{4\pi}\frac{2(1-\vec{\beta}_f\cdot\vec{\... ...eta}_i)}{1-\vert\vec{\beta}_fx + \vec{\beta}_i(1-x)\vert^2} .$$ (7.212)

In the soft photon limit $\beta_i=\beta_f\equiv\beta$ and $\vec{\beta}_i\cdot\vec{\beta}_f = \beta^2\cos\theta_f$. Thus

$$\int\frac{d\Omega_k}{4\pi}\frac{2(1-\vec{\beta}_f\cdot\vec{\... ...2\cos\theta)}{1-\beta^2 + 4\beta^2 \sin^2(\theta/2) x(1-x)} .$$ (7.213)

In the non-relativistic limit ($\beta\ll 1$) the integral (equation 7.213) becomes

$$\approx 2(1-\beta^2\cos\theta) \int_0^1 dx [1+\beta^2-4\beta^2\sin^2(\theta/2)x(1-x)]$$

$$\approx 2[1-\beta^2\cos\theta+\beta^2-2/3\beta^2\sin^2(\theta/2)]$$

$$= 2\left( 1 + \frac{4}{3} \beta^2 \sin^2\frac{\theta}{2} \right) + \mathcal{O}(\beta^4) \quad\textrm{for}\quad \beta\ll 1.$$ (7.214)

In the extreme relativistic limit

$$q^2 = (p_f-p_i)^2 = m^2 + m^2 -2E_fE_i +2\vec{p}_f\cdot\vec{p}_i$$

$$\approx -2E_fE_i(1-\cos\theta)$$

$$\approx -4E^2\sin^2(\theta/2)$$ (7.215)

and

$$-\frac{q^2}{m^2} = \frac{4}{1-\beta^2}\sin^2(\theta/2)$$ (7.216)

and the integral (equation 7.213) becomes

$$\approx -\frac{q^2}{m^2} \int_0^1 \frac{dx}{1+(-q^2/m^2)x(1-x)} .$$ (7.217)

From a table of integrals

$$\int\frac{dx}{a+bx+cx^2} = \frac{1}{\sqrt{-d}}\ln\frac{2cx+b-\sqrt{-d}} {2cx+b+\sqrt{-d}} \quad\textrm{if}\quad d<0$$ (7.218)

where $d=4ac-b^2$. Including the limits of integration we have

$$\int_0^1\frac{dx}{a+bx+cx^2} = \frac{1}{\sqrt{-d}}\ln \frac{(2c+b-\sqrt{-d})(b+\sqrt{-d})}{(2c+b+\sqrt{-d})(b-\sqrt{-d})} .$$ (7.219)

For the case of $a=1$ and $c=-b$

$$\int_0^1\frac{dx}{1+bx(1-x)} = \frac{2}{\sqrt{-d}}\ln \frac{b+\sqrt{-d}}{b-\sqrt{-d}} ,$$ (7.220)

where $-d=b^2(1+4/b)$. In our case $b=-q^2/m^2$ and $\sqrt{-d}\approx\vert b\vert(1+2/b)$. Thus

$$\int_0^1\frac{dx}{1+bx(1-x)} = \frac{4}{\vert b\vert}\ln\vert b\vert + \mathcal{O}\left(\frac{1}{b}\right) .$$ (7.221)

The integral (equation 7.213) now becomes

$$\approx 4\ln\left(\frac{-q^2}{m^2}\right) + \mathcal{O}\left(\frac{m^2}{q^2}\right) ,$$ (7.222)

Therefore the soft bremsstrahlung cross-section is

$$\frac{d\sigma}{d\Omega_f} = \left( \frac{d\sigma}{d\Omega_f}... ...{m^2}{q^2}\right) & \frac{m^2}{q^2}\ll 1 \end{array}\right. .$$ (7.223)