Photon-Electron Scattering

Electrodynamic processes can be classified by the number and type of particles in the initial state. Our goal in this chapter is to consider the two-particle initial states that led to scattering processes. Photon-electron scattering will be considered in this section, while the photon-photon and electron-electron systems will be consider in subsequent sections. Our use of the word ``electron'' has been generic and includes both electrons and positrons, in general.

The photon-electron system can have two kinds of final states, those in which there is only one electron present (and one or more photons), and those in which there are also one or more electron-positron pairs present. Processes leading to the former kind of final states may be called photon-electron scattering, whereas processes in which pairs are produced can be referred to as pair production in photon-electron collisions.

Photon-electron scattering with only one photon in the final state is the lowest-order photon-electron process involving a real incident photon. The separation of the lowest-order from the higher order contributions is an idealization which does not correspond to physical reality. In any measurement, the energy of the final state can only be determined to within the energy resolution of the detector. It is therefore impossible to determine with certainty whether the final state contains exactly one photon or whether it contains an additional number of very soft (low energy) photons. These multiple-photon final states are suppressed relative to the lowest-order single-photon final state by at least order $\alpha$.

The lowest order photon-electron scattering process is second-order in $\alpha$ and is called Compton scattering. The Compton scattering process differs from Bremsstrahlung in that the incoming photon is real. Because of charge conjugation invariance of the $S$-matrix, the cross-section for the photon-electron process is equal to the cross-section for the photon-positron process.

Figure 7.7 shows the two diagrams leading to Compton scattering. It is important to realize that only the sum of the two diagrams in figure 7.7 describes photon-electron scattering. The separation of a matrix element into terms corresponds to the individual diagrams, though extremely useful, has in general no physical meaning. Only the sum of both diagrams is observable.

Figure 7.7: Feynman diagrams for Compton scattering.

In the first diagram (figure 7.7a), the incident photon ($k,\varepsilon$) is absorbed by the incident electron ($p_i,s_i$) and then the electron emits a photon ( $k^\prime,\varepsilon^\prime$) into the final state. In the second diagram (figure 7.7b), the incident electron ($p_i,s_i$) emits a photon ( $k^\prime,\varepsilon^\prime$) before it absorbs the incident photon ($k,\varepsilon$). Since each photon is associated with a different momentum four-vector and each electron path can be labeled as refering to the first, second or third electrons, we have two distinct Feynman diagrams in figure 7.7. The two diagrams are different since they differ in the sequence of the emitted and absorbed photons as one follows the arrows in the electron paths. One can draw the second diagram such that the intermediate electron is horizontal in the diagram and the two photon do not cross in the diagram. This horizontal-electron diagram is not topologically different from the diagram in figure 7.7b and will not be considered further. Compton scattering is thus the process $e\gamma\rightarrow e\gamma$, in which the conservation of energy-momentum requires $p_i+k=p_f+k^\prime$.

Let $A^\mu(x;k)$ represent an incident photon which is absorbed by an electron at one vertex and $A^\prime_\mu(x^\prime;k^\prime)$ represent a final photon emitted at the second vertex:

$$A^\mu(x;k) = \frac{\varepsilon^\mu}{\sqrt{2\omega V}} (e^{-i... ...(e^{-ik^\prime\cdot x^\prime} + e^{ik^\prime\cdot x^\prime}) ,$$ (7.224)

where $\omega = k_0$ and $\omega^\prime = k_0^\prime$.

The second-order Compton amplitude is, after carrying out the Fourier transformation to momentum space,

$$S_{fi} = e^2\int d^4y d^4x \overline{\psi}_f(y) [ (-i\not{\!\!A}(y;k^\prime)) iS_F(y-x) (-i\not{\!\!A}(x;k))$$

$$+ (-i\not{\!\!A}(y;k)) iS_F(y-x) (-i\not{\!\!A}(x;k^\prime))] \psi_i(x) ,$$

$$= e^2\int d^4y d^4x \sqrt{\frac{m}{E_fV}} \overline{u}(p_f,s_f) e^{... ...) \int\frac{d^4q}{(2\pi)^4} e^{-iq\cdot(y-x)} \frac{i}{\not{\;\!\!q}-m} \right.$$

$$\cdot \frac{-i\not{\varepsilon}} {\sqrt{2\omega V}} (e^{-ik\cdot x} + e... ...cdot y}) \int \frac{d^4q}{(2\pi)^4} e^{-iq\cdot(y-x)} \frac{i}{\not{\;\!\!q}-m}$$

$$\cdot \left. \frac{-i\not{\varepsilon}^\prime}{\sqrt{2\omega^\prime V}}... ...^{ik^\prime\cdot x}) \right] \sqrt{\frac{m}{E_iV}} u(p_i,s_i) e^{-ip_i\cdot x}.$$ (7.225)

Each term in equation 7.225 represents one of the eight diagrams shown in figure 7.8. Not every term that occurs in the scattering amplitude is physically relevant to the process considered. The first two diagrams (figures 7.8a and 7.8b) are the processes we are interested in when studying Compton scattering. The second pair of diagrams (figures 7.8c and 7.8d) have the photon momenta $k$ and $k^\prime$ interchanged. This interchange of momenta corresponds to the scattering of an incident photon with momentum $k^\prime$ to a final photon with momentum $k$. The process represented by these diagrams is not the physical process that we are interested in and has energy-momentum conserving conditions that are incompatible with the process we are interested in. We thus drop these terms from the scattering amplitude since they are not the process under study. The third and fourth pairs of diagrams have two photons in the final state (figures 7.8e and 7.8f) and two photons in the initial state (figures 7.8g and 7.8h), respectively. These processes are not kinematically allowed. Such terms in the scattering amplitude contain delta functions with an argument describing these kinematically forbidden processes. The delta functions cause these terms to vanish when the momenta is integrated over.

Figure 7.8: Possible terms in the $S$-matrix for Compton scattering.

For the diagrams we are interested in, we retain from the incident photon wave function only the first term, $e^{-ik\cdot x}$, which corresponds to absorption at $x$ of a photon of four-momentum $k^\mu$ from the radiation field, and retain from the final photon wave function only the second term, $e^{ik^\prime\cdot x^\prime}$, which represents the emission at $x^\prime$ of a photon with four-momentum $k^\prime$.

The amplitude now becomes

$$S_{fi} = e^2\int d^4y d^4x \sqrt{\frac{m}{E_fV}} \overline{u}(p_f,s_f) e^{... ...m} \frac{-i\not{\;\!\!\!\varepsilon}} {\sqrt{2\omega V}} e^{-ik\cdot x} \right.$$

$$+ \left. \frac{-i\not{\;\!\!\!\varepsilon}}{\sqrt{2\omega V}} e^{-i... ...^{ik^\prime\cdot x} \right] \sqrt{\frac{m}{E_iV}} u(p_i,s_i) e^{-ip_i\cdot x} ,$$

$$= \frac{e^2}{V^2} \int d^4y d^4x \frac{d^4q}{(2\pi)^4} \sqrt{\frac{... ...ine{u}(p_f,s_f) \left[ e^{iy\cdot(p_f+k^\prime-q)} e^{ix\cdot(q-k-p_i)} \right.$$

$$\cdot \left. (-i\not{\;\!\!\!\varepsilon}^\prime) \frac{i}{\not{\;\!\!q... ...c{i}{\not{\;\!\!q}-m} (-i\not{\;\!\!\!\varepsilon}^\prime) \right] u(p_i,s_i) ,$$

$$= \frac{e^2}{V^2} \int (2\pi)^4 d^4q \sqrt{\frac{m^2}{E_fE_i}} \fra... ...+k^\prime-q) \delta^{(4)}(q-k-p_i) (-i\not{\;\!\!\!\varepsilon}^\prime) \right.$$

$$\cdot \left. \frac{i}{\not{\;\!\!q}-m} (-i\not{\;\!\!\!\varepsilon}) + ... ...c{i}{\not{\;\!\!q}-m} (-i\not{\;\!\!\!\varepsilon}^\prime) \right] u(p_i,s_i) ,$$

$$= \frac{e^2}{V^2} \sqrt{\frac{m^2}{E_fE_i}} \frac{1}{\sqrt{2\omega ... ...c{i}{\not{\;\!\!\!p}_i+\not{\;\!\!\!k}-m} (-i\not{\;\!\!\!\varepsilon}) \right.$$

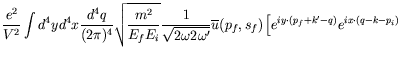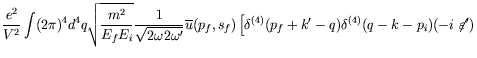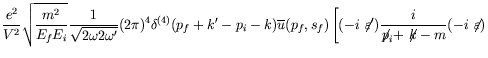$$+ \left. (-i\not{\;\!\!\!\varepsilon}) \frac{i}{\not{\;\!\!\!p}_i-\not{\;\!\!\!k}^\prime-m} (-i\not{\;\!\!\!\varepsilon}^\prime )\right] u(p_i,s_i) .$$ (7.226)

Notice that $S_{fi}$ is symmetric under interchange of $k$ and $\varepsilon$ with $-k^\prime$ and $\varepsilon^\prime$, respectively. The two diagrams in figure 7.7 are thus related by this symmetry. This is known as crossing symmetry, and it persists as an exact symmetry to all orders in $\alpha$.

We form the cross-section $d\sigma$ by squaring the amplitude, then dividing by $(2\pi)^4\delta^{(4)}(0) = VT$ to form a rate per volume. We then divide the rate by an incident flux $\vert\vec{v}_{\mathrm{rel}}\vert/V$, where $\vec{v}_{\mathrm{rel}}$ is the relative velocity of the photons with respect to the electrons. Then we divide by the number of target particles per unit volume $1/V$. Finally, summing over phase space of the final particles $(V^2/(2\pi)^6)d^3p_fd^3k^\prime$, $d\sigma$ becomes

$$d\sigma = \frac{\vert S_{fi}\vert^2}{(2\pi)^4\delta^{(4)}(0)V} \frac{V}{\vert\vec{v}_{\mathrm{rel}}\vert} \frac{V^2}{(2\pi)^6} d^3p_fd^3k^\prime ,$$

$$= \frac{e^4m}{(2\pi)^22\omega E_i\vert\vec{v}_{\mathrm{rel}}\vert} ... ...\!k}^\prime-m} \not{\;\!\!\!\varepsilon}^\prime \right) u(p_i,s_i)\right\vert^2$$

$$\cdot \delta^{(4)}(p_f+k^\prime-p_i-k) \frac{md^3p_f}{E_f} \frac{d^3k^\prime}{2\omega^\prime}$$

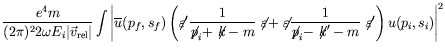$$= \frac{\alpha^2m^2}{\omega E_i\vert\vec{v}_{\mathrm{rel}}\vert} \i... ...(4)}(p_f+k^\prime-p_i-k) \frac{d^3p_f}{E_f} \frac{d^3k^\prime}{\omega^\prime} ,$$ (7.227)

where $\vert\mathcal{M}\vert^2$ is the invariant matrix element for Compton scattering. It is a function of the four-momenta $p_i, p_f, k$ and $k^\prime$.

We use $d^3k^\prime = \omega^{\prime^2} d\omega^\prime d\Omega$ to write the differential cross-section per unit solid angle for scattering into a differential angular interval between $\theta$ and $\theta+d\theta$, and $\phi$ and $\phi+d\phi$. The integral over all recoil electron momenta can be evaluated with the aid of the previously developed covariant expression

$$\frac{d^3p_f}{2E_f} = \int_{-\infty}^{+\infty} d^4p_f \delta(p_f^2-m^2)\theta({p_f}_0) .$$ (7.228)

The differential cross-section now becomes

$$\frac{d\sigma}{d\Omega} = \frac{2\alpha^2m^2}{\omega E_i\vert\vec{v}_{\mathrm{rel}}\vert} \... ...al{M}\vert^2 \delta^{(4)}(p_f+k^\prime-p_i-k) \delta(p_f^2-m^2) \theta({p_f}_0)$$

$$= \frac{2\alpha^2m^2}{\omega E_i\vert\vec{v}_{\mathrm{rel}}\vert} \... ...thcal{M}\vert^2 \delta[(p_i+k-k^\prime)^2-m^2] \theta(E_i+\omega-\omega^\prime)$$

$$= \frac{2\alpha^2m^2}{\omega E_i\vert\vec{v}_{\mathrm{rel}}\vert} \... ...rime} \vert\mathcal{M}\vert^2 \delta[2p_i\cdot(k-k^\prime) -2k\cdot k^\prime] ,$$ (7.229)

where the kinematic variables in the matrix element $\vert\mathcal{M}\vert^2$ must now obey the condition $p_i+k=p_f+k^\prime$.

The cross-section simplifies considerably if we calculate it in the rest system of the initial or final electron. In most experiments the initial electron is practically at rest in the laboratory so we will work in the rest frame of the initial electron. In this frame $p_i=(m,0)$, the incident beam consists of photons with unit velocity, such that $\vert\vec{v}_{\mathrm{rel}}\vert=1$. The differential cross-section now becomes

$$\frac{d\sigma}{d\Omega} = \frac{2\alpha^2m}{\omega} \int_0^{E_i+\omega} {d\omega^\prime}{\o... ...M}\vert^2 \delta[2m(\omega-\omega^\prime) - 2\omega\omega^\prime(1-\cos\theta)]$$

$$= \frac{2\alpha^2m}{\omega} \vert\mathcal{M}\vert^2 \frac{\omega^\prime}{\vert 2m + 2\omega(1-\cos\theta)\vert}$$

$$= \alpha^2 \left(\frac{\omega^\prime}{\omega}\right)^2 \vert\mathcal{M}\vert^2,$$ (7.230)

where $\theta$ is the angle between the initial and final state photons.

The last line in equation 7.230 was obtained by using the root of the delta function to relate $\omega$ to $\omega^\prime$:

$$\omega^\prime = \frac{\omega}{1+(\omega/m)(1-\cos\theta)} = \frac{\omega}{1+(2\omega/m)\sin^2(\theta/2)} .$$ (7.231)

This is known as the Compton condition. This kinematic relationship takes on a simple form if one uses the wavelength, $\lambda = 2\pi/\omega$:

$$\lambda^\prime = \lambda + \frac{2\pi}{m} (1-\cos\theta) .$$ (7.232)

This is the familiar Compton formula. The wavelength of the scattered photon is increased by an amount of order $1/m$, and $\hbar/mc$ is called the Compton wavelength.

The differential cross-section for electrons and photons with specific initial and final state polarizations is now

$$\frac{d\sigma}{d\Omega} = \alpha^2 \left(\frac{\omega^\prime... ...\;\!\!\!\varepsilon}^\prime \right) u(p_i,s_i)\right\vert^2 .$$ (7.233)

We can simplify the spinor matrix element considerably by choosing the special gauge in which both initial and final photons are transversely polarized in the laboratory frame. We choose

$$\varepsilon^\mu = (0,\vec{\varepsilon}) \quad\textrm{so that}\quad \vec{\varepsilon}\cdot\vec{k} = 0 \quad\textrm{and}$$ (7.234)

$$\varepsilon^{\mu^\prime} = (0,\vec{\varepsilon}^\prime) \quad\textrm{so that}\quad \vec{\varepsilon}^\prime\cdot\vec{k}^\prime = 0 .$$ (7.235)

Since the electron is initially at rest it follows that

$$\varepsilon\cdot p_i = \varepsilon^\prime\cdot p_i = 0 .$$ (7.236)

This amounts to choosing the ``radiation gauge'' in which the electromagnetic potential has no time component. However, the condition in equation 7.236 can be imposed in any given frame of reference. This can be shown by applying a gauge transformation to any arbitrary set of polarization vectors $\varepsilon$ and $\varepsilon^\prime$. The normalization and transversality conditions are not effected by the transformation. Thus without restricting the generality of our calculation we will impose the condition in equation 7.236.

Because of our choice of gauge, $\not{\;\!\!\!k}$ and $\not{\;\!\!\!p}_i$ anticommute with $\not{\;\!\!\!\varepsilon}$, and $\not{\;\!\!\!k}^\prime$ and $\not{\;\!\!\!p}_i^\prime$ anticommute with $\not{\;\!\!\!\varepsilon}^\prime$. The invariant matrix element thus becomes

$$\mathcal{M} = \overline{u}(p_f,s_f) \left( \not{\;\!\!\!\varepsilon}^\prime \fr... ...ime+m}{-2k^\prime\cdot p_i} \not{\;\!\!\!\varepsilon}^\prime \right) u(p_i,s_i)$$

$$= \overline{u}(p_f,s_f) \left( \not{\;\!\!\!\varepsilon}^\prime\not... ...{\;\!\!\!p}_i+\not{\;\!\!\!k}^\prime+m}{-2k^\prime\cdot p_i} \right) u(p_i,s_i)$$

$$= -\overline{u}(p_f,s_f) \left( \frac{\not{\;\!\!\!\varepsilon}^\pr... ...epsilon}^\prime\not{\;\!\!\!k}^\prime}{2k^\prime\cdot p_i} \right) u(p_i,s_i) ,$$ (7.237)

where the energy-projection operator $(-\not{\;\!\!\!p}+m)u(p,s)=0$ has been used in the last step.

We now consider the case when the electrons are unpolarized but the initial and final state photons may be polarized with polarizations $\lambda$ and $\lambda^\prime$, respectively. We thus average over the initial electron spin and sum over the final electron spin:

$$\frac{d\overline{\sigma}}{d\Omega}(\lambda,\lambda^\prime) = \frac{1}{2} \sum_{\pm s_i,\pm s_f} \frac{d\sigma}{d\Omega} .$$ (7.238)

Applying the usual trace techniques, we have

$$\frac{d\overline{\sigma}}{d\Omega}(\lambda,\lambda^\prime) =... ...ot{\;\!\!\!\varepsilon}}{2k^\prime\cdot p_i} \right)\right] .$$ (7.239)

where we have used the rule $\overline{\not{a}\not{b}\not{c}} = \not{c}\not{b}\not{a}$ in the last factor.

There are traces with up to eight $\gamma$-matrices in them. To reduce the traces which contain the same vectors, we commute the $\gamma$-matrices until the identical vectors are alongside each other, then the identity $\not{\;\!\!a}\not{\;\!\!a}=a^2$ removes two $\gamma$-matrices. We also make use of $k^2=0$, $\varepsilon^2= \varepsilon^{\prime^2}=-1$, $k\cdot p_f = k^\prime\cdot p_i$ and $k\cdot\varepsilon^\prime = p_f\cdot\varepsilon^\prime$. Evaluating the traces one by one, we have

$$T_1 = \textrm{Tr}[(\not{\;\!\!\!p}_f+m)\not{\;\!\!\!\varepsilon}^\prime... ... + m) \not{\;\!\!\!k}\not{\;\!\!\!\varepsilon}\not{\;\!\!\!\varepsilon}^\prime]$$

$$= \textrm{Tr}[\not{\;\!\!\!p}_f\not{\;\!\!\!\varepsilon}^\prime \no... ...\!\!k}\not{\;\!\!\!k}\not{\;\!\!\!\varepsilon}\not{\;\!\!\!\varepsilon}^\prime]$$

$$= 2k\cdot p_i\textrm{Tr}[\not{\;\!\!\!p}_f \not{\;\!\!\!\varepsilon... ...ilon}\not{\;\!\!\!k} \not{\;\!\!\!\varepsilon}\not{\;\!\!\!\varepsilon}^\prime]$$

$$= 2k\cdot p_i\textrm{Tr}[\not{\;\!\!\!p}_f \not{\;\!\!\!\varepsilon}^\prime \not{\;\!\!\!k} \not{\;\!\!\!\varepsilon}^\prime]$$

$$= 2k\cdot p_i ( \textrm{Tr}[\not{\;\!\!\!p}_f\not{\;\!\!\!k}] + 2k\... ...arepsilon^\prime\textrm{Tr}[\not{\;\!\!\!p}_f\not{\;\!\!\!\varepsilon}^\prime])$$

$$= 8k\cdot p_i(p_f\cdot k + 2k\cdot\varepsilon^\prime p_f\cdot\varepsilon^\prime)$$

$$= 8k\cdot p_i[k^\prime\cdot p_i + 2(k\cdot\varepsilon^\prime)^2] .$$ (7.240)

Using the symmetry we had earlier $\varepsilon,k \leftrightarrow \varepsilon^\prime,-k^\prime$ we have

$$T_2 = \textrm{Tr}[ (\not{\;\!\!\!p}_f + m) \not{\;\!\!\!\varepsilon}\no... ...t{\;\!\!\!k}^\prime \not{\;\!\!\!\varepsilon}^\prime \not{\;\!\!\!\varepsilon}]$$

$$= 8k^\prime\cdot p_i [k\cdot p_i - 2(k^\prime\cdot\varepsilon)^2] .$$ (7.241)

We show that the two cross-terms are equal:

$$T_3 = \textrm{Tr} (\not{\;\!\!\!p}_f + m) \not{\;\!\!\!\varepsilon}^\pr... ...ot{\;\!\!\!k}^\prime \not{\;\!\!\!\varepsilon}^\prime \not{\;\!\!\!\varepsilon}$$

$$= \textrm{Tr} \not{\;\!\!\!\varepsilon}\not{\;\!\!\!\varepsilon}^\p... ...ot{\;\!\!\!\varepsilon}\not{\;\!\!\!\varepsilon}^\prime (\not{\;\!\!\!p}_f + m)$$

$$= \textrm{Tr} (\not{\;\!\!\!p}_f + m) \not{\;\!\!\!\varepsilon}\not... ... + m)\not{\;\!\!\!k}\not{\;\!\!\!\varepsilon}\not{\;\!\!\!\varepsilon}^\prime .$$ (7.242)

Using energy-momentum conservation we have

$$T_3 = \textrm{Tr} (\not{\;\!\!\!p}_f + m) \not{\;\!\!\!\varepsilon}^\pr... ...ot{\;\!\!\!k}^\prime \not{\;\!\!\!\varepsilon}^\prime \not{\;\!\!\!\varepsilon}$$

$$= \textrm{Tr} (\not{\;\!\!\!p}_i + \not{\;\!\!\!k}- \not{\;\!\!\!k}... ...ot{\;\!\!\!k}^\prime \not{\;\!\!\!\varepsilon}^\prime \not{\;\!\!\!\varepsilon}$$

$$= \textrm{Tr} (\not{\;\!\!\!p}_i + m) \not{\;\!\!\!\varepsilon}^\pr... ...ot{\;\!\!\!k}^\prime \not{\;\!\!\!\varepsilon}^\prime \not{\;\!\!\!\varepsilon}$$

$$= \textrm{Tr} (\not{\;\!\!\!p}_i + m) \not{\;\!\!\!k}(\not{\;\!\!\!... ...t{\;\!\!\!k}^\prime \not{\;\!\!\!\varepsilon}^\prime \not{\;\!\!\!\varepsilon}]$$

$$- 2k\cdot\varepsilon^\prime \textrm{Tr}[ \not{\;\!\!\!k}\not{\;\!\!... ...ot{\;\!\!\!\varepsilon}\not{\;\!\!\!k}\not{\;\!\!\!p}_i \not{\;\!\!\!k}^\prime]$$

$$= -\textrm{Tr} (\not{\;\!\!\!p}_i - m) \not{\;\!\!\!k}(\not{\;\!\!\... ...;\!\!\!\varepsilon} \not{\;\!\!\!\varepsilon}^\prime \not{\;\!\!\!\varepsilon}]$$

$$- 8k\cdot\varepsilon^\prime [ k\cdot\varepsilon^\prime p_i\cdot k^\prime] + 8k^\prime\cdot\varepsilon [ \varepsilon\cdot k^\prime k\cdot p_i ]$$

$$= -2k\cdot p_i \textrm{Tr}[ \not{\;\!\!\!p}_i \not{\;\!\!\!k}^\prim... ...repsilon^\prime)^2 k^\prime\cdot p_i + 8(k^\prime\cdot\varepsilon)^2 k\cdot p_i$$

$$= -8k\cdot p_i p_i\cdot k^\prime] + 16k\cdot p_i \varepsilon\cdot\v... ...repsilon^\prime)^2 k^\prime\cdot p_i + 8(k^\prime\cdot\varepsilon)^2 k\cdot p_i$$

$$= 8(k\cdot p_i)(k^\prime\cdot p_i)[2(\varepsilon^\prime\cdot\vareps... ...psilon^\prime)^2 k^\prime\cdot p_i + 8(k^\prime\cdot\varepsilon)^2 k\cdot p_i .$$ (7.243)

Therefore the differential cross-section becomes

$$\frac{d\overline{\sigma}}{d\Omega}(\lambda,\lambda^\prime) = \frac{\alpha^2}{4m^2} \left(\frac{\omega^\prime}{\omega}\right)^2... ...} + \frac{k\cdot p_i -2(k^\prime\cdot\varepsilon)^2}{k^\prime\cdot p_i} \right.$$

$$+ \left. 2[2(\varepsilon^\prime\cdot\varepsilon)^2 - 1] -2\frac{(k\... ...}{k\cdot p_i} + 2\frac{(k^\prime\cdot\varepsilon)^2}{k^\prime\cdot p_i} \right]$$

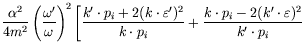$$= \frac{\alpha^2}{4m^2}\left(\frac{\omega^\prime}{\omega}\right)^2 ... ... p_i}{k^\prime\cdot p_i} + 4(\varepsilon^\prime\cdot\varepsilon)^2 - 2\right] .$$ (7.244)

The calculation of the invariant matrix element has so far been covariant. In the rest frame of the initial electron the differential cross-section becomes

$$\fbox{$\displaystyle \frac{d\overline{\sigma}}{d\Omega}(\lam... ...e} + 4(\varepsilon^\prime\cdot\varepsilon)^2 - 2\right] $}\ ,$$ (7.245)

which is the Klein-Nishina formula for Compton scattering.

In the low-energy limit of $\omega\rightarrow 0$, equation 7.231 shows that $\omega^\prime/\omega\rightarrow 1$ and the cross-section reduces to the classical Thomson scattering

$$\fbox{$\displaystyle \left(\frac{d\overline{\sigma}}{d\Omega... ...c{\alpha^2}{m^2} (\varepsilon\cdot\varepsilon^\prime)^2 $}\ ,$$ (7.246)

where

$$r_0 \equiv \frac{\alpha}{m} = \frac{e^2}{4\pi mc^2} = 2.8\times 10^{-13} \ \textrm{cm}$$ (7.247)

is the classical electron radius.

For forward scattering, $\theta\rightarrow 0$ and according to equation 7.231 $\omega\rightarrow \omega^\prime$. The Thomson cross-section is thus also valid for forward scattering at all energies.

Returning to the general expression for the cross-sections, we can sum over final-state photon polarizations $\varepsilon^\prime_{\lambda^\prime}$ and average over initial-state polarizations $\varepsilon_\lambda$ to obtain the unpolarized cross-section.

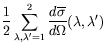$$\frac{d\overline{\sigma}}{d\Omega} = \frac{1}{2} \sum_{\lambda,\lambda^\prime=1}^2 \frac{d\overline{\sigma}}{d\Omega}(\lambda,\lambda^\prime)$$

$$= \frac{\alpha^2}{8m^2} \left(\frac{\omega^\prime}{\omega}\right)^2... ...} + 4(\varepsilon_\lambda\cdot\varepsilon^\prime_{\lambda^\prime})^2 - 2\right]$$

$$= \frac{\alpha^2}{2m^2} \left(\frac{\omega^\prime}{\omega}\right)^2... ...^2 (\varepsilon_\lambda\cdot\varepsilon^\prime_{\lambda^\prime})^2 - 2\right] .$$ (7.248)

We can evaluate the remaining spin sum by supposing the incident photon arrives along the $z$-direction, while the final photon departs into the solid angle $d\Omega$ described by polar angles $\theta$ and $\phi$ such that

$$\hat{k} = (0,0,1),$$ (7.249)

$$\hat{k}^\prime = (\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta) .$$ (7.250)

We may select the associated polarization vectors to be

$$\vec{\varepsilon}_{(1)} = (1,0,0), \quad \varepsilon^\prime_{(1)} = (\sin\phi,-\cos\phi,0),$$ (7.251)

$$\vec{\varepsilon}_{(2)} = (0,1,0), \quad \varepsilon^\prime_{(2)} = (\cos\theta\cos\phi,\cos\theta\sin\phi,-\sin\theta).$$ (7.252)

It is easy to show that this choice of vectors satisfies all the required normalization and orthogonality relationships. We obtain

$$\sum_{\lambda,\lambda^\prime=1}^2 (\varepsilon_\lambda\cdot\... ...hi + \cos^2\phi + \cos^2\theta\sin^2\phi = 1 + \cos^2\theta .$$ (7.253)

The cross-section thus becomes

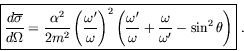$$\fbox{$\displaystyle \frac{d\overline{\sigma}}{d\Omega} = \f... ...ga} + \frac{\omega}{\omega^\prime} -\sin^2\theta \right) $}\ .$$ (7.254)

The low-energy for forward-scattering limit (classical limit) now becomes

$$\fbox{$\displaystyle \left(\frac{d\overline{\sigma}}{d\Omega... ...lass}} = \frac{r_0^2}{2} \left( 1 + \cos^2\theta \right) $}\ .$$ (7.255)

To integrate the differential cross-section, we simplify the notation by introducing $z=\cos\theta$, and use equation 7.231 to write

$$\overline{\sigma} = \frac{\pi\alpha^2}{m^2} \int_{-1}^1 dz \... ...omega/m)(1-z)} - \frac{1-z^2}{[1+(\omega/m)(1-z)]^2} \right].$$ (7.256)

To perform the integration, define $x=1-z$, then

$$\overline{\sigma} = \frac{\pi\alpha^2}{m^2} \int_0^2 dx \lef... ...1}{1+(\omega/m)x} + \frac{x^2-2x}{[1+(\omega/m)x]^2} \right].$$ (7.257)

Using the integrals ($b$ is an arbitrary constant)

$$\int\frac{dx}{1+bx} = \left.\frac{1}{b}\ln(1+bx)\right\vert _0^2 = \frac{1}{b}\ln(1+2b) ,$$ (7.258)

$$\int\frac{dx}{(1+bx)^3} = -\left.\frac{1}{2b(1+bx)^2}\right\vert _0^2 = \frac{1}{2b} \left[ 1 - \frac{1}{(1+2b)^2} \right] ,$$ (7.259)

$$\int\frac{x^2dx}{(1+bx)^2} = \left.\frac{1}{b^3} \left[ 1+bx-2\ln(1+bx) -\frac{1}{1+bx} \right]\right\vert _0^2$$

$$= \frac{1}{b^3} \left[ 2b -2\ln(1+2b) -\frac{1}{1+2b} + 1 \right] ,$$ (7.260)

$$\int\frac{xdx}{(1+bx)^2} = \frac{1}{b^2} \left.\left[ \ln(1+bx) + \frac{1}{1+bx} \right]\right\vert _0^2 = \frac{1}{b^2} \left[ \ln(1+2b) + \frac{1}{1+2b} - 1 \right] ,$$ (7.261)

we can write

$$\overline{\sigma} = \frac{\pi\alpha^2}{m^2} \left(\frac{m}{\omega}\right)^3 \left\{ 1 -\frac{1}{1+2(\omega/m)} -2\ln\left(1+2\frac{\omega}{m}\right) \right.$$

$$+ 2 \left(\frac{\omega}{m}\right) \left[ 2 -\frac{1}{1+2(\omega/m)} - \ln\left(1+2\frac{\omega}{m}\right) \right]$$

$$+ \left.\frac{1}{2} \left(\frac{\omega}{m}\right)^2 \left[ 1 -\frac{1}{[1+2(\omega/m)]^2} + 2\ln\left(1+2\frac{\omega}{m}\right) \right] \right\} ,$$ (7.262)

which is valid for all initial photon energies $\omega$.

For low energies, $\omega/m\rightarrow 0$ and

$$\overline{\sigma} \approx \frac{\pi\alpha^2}{m^2} \left(\frac{m}{\omega}\right)^3 \left\{ -... ...{\omega}{m}\right) +\frac{8}{3}\left(\frac{\omega}{m}\right)^3 + \cdots \right.$$

$$+ 2 \left. \left(\frac{\omega}{m}\right) \left[ 1 -2\left(\frac{\om... ...ga}{m}\right)^2 \left[ 8\left(\frac{\omega}{m}\right) + \cdots \right] \right\}$$

$$\approx \frac{8\pi}{3} \frac{\alpha^2}{m^2} = \frac{8\pi}{3} r_0^2 ,$$ (7.263)

which is again the classical Thomson cross-section.

At high energies, $m/\omega\rightarrow 0$ and

$$\overline{\sigma} \approx \frac{\pi\alpha^2}{m^2} \left(\frac{m}{\omega}\right)^3 \left\{ 2... ...{\omega}{m}\right)^2 \left[ 1 + 2\ln\frac{2\omega}{m} + \cdots \right] \right\}$$

$$\approx \frac{\pi\alpha^2}{\omega m} \left[ \ln\frac{2\omega}{m} + \frac{1}{2} + \mathcal{O} \left( \frac{m}{\omega} \ln\frac{\omega}{m} \right) \right] .$$ (7.264)