There are three essentially different kinds of pair annihilations. The first kind is the annihilation of a free positron with a free electron in relative motion towards each other; we shall call this the annihilation of free electron-positron pairs and shall discuss it here. Since the probability for the occurrence of this process increases with decreasing relative velocity, it will compete with the process of capture into the bound positronium state, which in turn can decay into photons. This positronium annihilation most likely occurs from one of the lowest energy levels (S-state) and will always be governed by selection rules. Finally, the third kind of annihilation takes place in the presence of an external field, e.g. the Coulomb field of a nucleus. This pair annihilation in an external field is of importance when positrons annihilate with tightly bound electrons whose binding to the nucleus cannot be neglected. This latter process is the only one in which energy-momentum conservation does not exclude one-photon annihilation, i.e. pair annihilation with the emission of only one photon.
Consider the process of annihilation of an electron-positron pair into
two gamma rays, as shown in figure 7.9.
This is the lowest order in ![]() in which this process can occur,
since pair annihilation to a single photon cannot conserve energy and
momentum:
in which this process can occur,
since pair annihilation to a single photon cannot conserve energy and
momentum:
![]() but
but ![]() .
The diagrams can be view as Compton scattering turn on its side.
.
The diagrams can be view as Compton scattering turn on its side.
Using our previously determined Feynman rules, we can write down the
relevant ![]() -matrix element in momentum space from inspection of the
diagram in figure 7.9:
-matrix element in momentum space from inspection of the
diagram in figure 7.9:
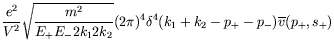 |
|||
| (7.265) |
We notice that the ![]() -matrix element is symmetric under interchange
of the two photons, which is required by Bose statistics.
Both graphs must be included in order to ensure this required
symmetry.
-matrix element is symmetric under interchange
of the two photons, which is required by Bose statistics.
Both graphs must be included in order to ensure this required
symmetry.
Compared to Compton scattering the substitutions
| (7.266) | |||
| (7.267) | |||
| (7.268) | |||
| (7.269) |
transform the two amplitudes into each other.
This is an example of a general substitution rule which is valid to
arbitrary order and which relates processes of the type
![]() to the process
to the process
![]() , where
, where ![]() denotes the antiparticle to
denotes the antiparticle to ![]() , etc.
, etc.
By familiar steps, we proceed from the matrix element to a differential cross-section
| (7.270) |
For an electron at rest
| (7.271) |
where
![]() is the incident positron velocity.
The invariant amplitude is
is the incident positron velocity.
The invariant amplitude is
| (7.272) |
where we have used
![]() .
For an unpolarized positron incident on an unpolarized electron, we
average over the initial spins
.
For an unpolarized positron incident on an unpolarized electron, we
average over the initial spins ![]() and
and ![]() .
Representing the quantity in square brackets as
.
Representing the quantity in square brackets as ![]() , we can write
, we can write
| (7.273) |
The unpolarized cross-section becomes
| (7.274) |
Notice the minus sign which comes for our normalization of the
positron spinors.
The simplified form of the matrix element is due to the choice of
transverse gauge
![]() for
the laboratory frame of reference and is the same gauge used in the
Compton scattering calculation.
We can thus obtain the trace directly from our previous result using
the substitutions above:
for
the laboratory frame of reference and is the same gauge used in the
Compton scattering calculation.
We can thus obtain the trace directly from our previous result using
the substitutions above:
| (7.275) |
It remains to reduce the ![]() -function for laboratory kinematics:
-function for laboratory kinematics:
| (7.276) | |||
| (7.277) | |||
| (7.278) |
The ![]() -functions allows us to write (
-functions allows us to write (
![]() ,
,
![]() ,
,
![]() )
)
| (7.279) | |||
| (7.280) | |||
| (7.281) |
Combining the above expressions gives
| (7.282) |
The angle between the two photons, ![]() , can be found from
, can be found from
| (7.283) |
This leads to
| (7.284) |
The sum over the final polarization states in the rest system gives (cf. equation 7.253)
| (7.285) |
and a factor of 4 for those terms which are independent of
![]() and
and ![]() , where
, where ![]() is the angle between the
photons.
We now have
is the angle between the
photons.
We now have
| (7.286) |
We now express the cross-section in terms of the energies of the two photons. Simple kinimatics gives
| (7.287) | |||
| (7.288) |
The differential cross-section in terms of photons energies becomes
| (7.289) |
For a total cross-section, we sum
![]() over
final photon polarizations and integrate over the solid angle.
Since the final state contains two identical particles, one of the
photons emerges in
over
final photon polarizations and integrate over the solid angle.
Since the final state contains two identical particles, one of the
photons emerges in ![]() ; because of their
indistinguishability, this can be either of the two photons.
If we were to integrate
; because of their
indistinguishability, this can be either of the two photons.
If we were to integrate
![]() over the entire
over the entire
![]() solid angle, we would be counting each distinguishable state
exactly twice.
We therefore take one-half of this integral in forming a total
cross-section
solid angle, we would be counting each distinguishable state
exactly twice.
We therefore take one-half of this integral in forming a total
cross-section
| (7.290) |
We now integrate the differential cross-section using:
| (7.291) | |||
| (7.292) | |||
| (7.293) |
Using these integrals we have
![$\displaystyle \frac{\pi\alpha^2}{m^2\beta^2\gamma(\gamma+1)}
\left[ \left(\gamm...
...}{\gamma}\right)
\ln\sqrt{\frac{1+\beta}{1-\beta}} - \beta (\gamma + 3) \right]$](img4475.png) |
|||
| (7.294) |
For incident positrons of low energy,
![]() and
and
![]() giving
giving
| (7.295) |
In the extreme relativistic limit, ![]() and
and
![]() giving
giving
| (7.296) |