Having developed the nonrelativistic propagator, we now turn to the development of the relativistic propagators. To delay the slight complication introduced by the Dirac matrices, we first develop the Klein-Gordon propagator. We will only consider the free-particle Klein-Gordon propagator in this section.
The free-particle Klein-Gordon propagator,
![]() ,
is defined to satisfy the Green's function equation
,
is defined to satisfy the Green's function equation
The minus sign on the right-hand side of equation 6.45 is choosen by convention since equation 4.69 also has a minus sign on the right-hand side. In addition to satisfying equation 6.45, the propagator must also only propagate positive-energy solutions forward in time and only propagate negative-energy solutions backward in time.
Rather than solve the Green's function equation in configuration space, we work in momentum space. The momentum-space representation will be totally adequate for our purposes since we will never require the explicit form of the propagators in configuration space.
The Fourier transform of the momentum-space propagator,
![]() , into configuration space is
, into configuration space is
| (6.46) |
Substituting this Fourier transform into equation 6.45, performing the differentiations, and representing the delta function as a Fourier transform gives
| (6.47) |
Therefore
| (6.48) | |||
| (6.49) |
provided ![]() .
There is a singularity at
.
There is a singularity at
![]() .
Or in other words, when
.
Or in other words, when
![]() .
This means that the particle represented by the Green's function is off
mass-shell, and
.
This means that the particle represented by the Green's function is off
mass-shell, and ![]() and
and ![]() are independent variables.
The origin of negative-energy waves in relativistic theories is the
pole at
are independent variables.
The origin of negative-energy waves in relativistic theories is the
pole at ![]() , which was not present in the nonrelativistic theory.
, which was not present in the nonrelativistic theory.
A prescription for how to handle the singularities is need to complete
the definition of the propagator.
The interpretation given to the Green function
![]() is that it represents the wave produced at
the point
is that it represents the wave produced at
the point ![]() by a unit source located at
by a unit source located at ![]() .
A necessary physical requirement is that the wave propagating from
.
A necessary physical requirement is that the wave propagating from ![]() into the future consist only of positive-energy components.
The boundary conditions on the integration of
into the future consist only of positive-energy components.
The boundary conditions on the integration of
![]() provide this requirement.
provide this requirement.
One can evaluate
![]() by Cauchy integration in the
by Cauchy integration in the
![]() -plane.
We perform the
-plane.
We perform the ![]() integration along the contour in the complex
integration along the contour in the complex
![]() -plane, which is infinitesimal close to the real axis and avoids
the poles at
-plane, which is infinitesimal close to the real axis and avoids
the poles at ![]() in some way.
As shown in figure 6.5, we close the contour with a semi-circle
at infinity: above for
in some way.
As shown in figure 6.5, we close the contour with a semi-circle
at infinity: above for ![]() and below for
and below for ![]() .
Only the positive pole contributes for
.
Only the positive pole contributes for ![]() and only the
negative pole contributes for
and only the
negative pole contributes for ![]() .
After the contour integration has been performed, one must take the
limit as the contour approaches the real axis and the enclosed
semi-circle approaches infinity along the imaginary axis.
.
After the contour integration has been performed, one must take the
limit as the contour approaches the real axis and the enclosed
semi-circle approaches infinity along the imaginary axis.
![\begin{figure}\begin{center}
\begin{picture}(455,190)(5,-10)
\SetWidth{0.75}
% L...
...ext(100,0)[c]{$t^\prime>t$}
\end{picture}}
\end{picture}\end{center}\end{figure}](img2681.png) |
For ![]() , the contour is closed in the lower half-plane and
includes the positive-energy pole at
, the contour is closed in the lower half-plane and
includes the positive-energy pole at
![]() only.
The factor
only.
The factor
![]() in the integrand will vanish as
in the integrand will vanish as
![]() , if
, if ![]() .
Performing the integral in this case, we have
.
Performing the integral in this case, we have
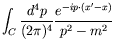 |
|||
![$\displaystyle \lim_{\epsilon\rightarrow 0} \left
[ \int_{-\infty-i\epsilon}^{0-...
...\epsilon} \frac{d^4p}{(2\pi)^4}
\frac{e^{ip\cdot(x^\prime-x)}}{p^2-m^2} \right]$](img2691.png) |
|||
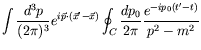 |
|||
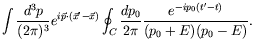 |
(6.50) |
Using Cauchy's integral formula for the pole at ![]() gives
gives
where the minus sign comes from the clockwise direction of the contour enclosing the pole.
For ![]() , the contour is close in the upper half-plane and
includes the negative-energy pole at
, the contour is close in the upper half-plane and
includes the negative-energy pole at
![]() .
The factor
.
The factor
![]() in the integrand will vanish as
in the integrand will vanish as
![]() , if
, if ![]() .
Performing the integral in this case, we have
.
Performing the integral in this case, we have
Notice that the only difference between the result of the two
integrations is the sign of ![]() in the exponential.
in the exponential.
We point out that any other choice of the integration contour, for example those shown in figure 6.6, would lead to contributions from negative-energy waves propagating into the future (figure 6.6a) or positive-energy waves propagating into the past (figure 6.6b).
An equivalent procedure for performing the integration along the real axis
is to displace the poles slightly away from the axis by a small real
number ![]() :
:
| (6.53) | |||
This procedure is shown in figure 6.7.
After the integration one takes the limit as the poles approach the
real axis (
![]() ).
).
![\begin{figure}\begin{center}
\begin{picture}(270,180)(-20,0)
\SetWidth{0.75}
\pu...
...lon$}
\Text(175,55)[b]{$C$}
\end{picture}}
\end{picture}\end{center}\end{figure}](img2716.png) |
The procedure of displacing the poles from the real axis is equivalent
to adding a small positive imaginary part ![]() to the
denominator of the propagator and
to the
denominator of the propagator and
![]() is to be
taken at the end of the calculation:
is to be
taken at the end of the calculation:
| (6.54) |
Then the singularity corresponding to positive-energy states is
| (6.55) |
which lies below the real ![]() -axis, while the pole corresponding to
negative-energy states is
-axis, while the pole corresponding to
negative-energy states is
| (6.56) |
which is located above the ![]() -axis, as required.
-axis, as required.
![]() is another small positive real number.
is another small positive real number.
This prescription is most easily remembered in the form of a rule:
to ensure the correct boundary conditions, the mass has to be given a
small negative imaginary part (
![]() ).
Writing it this way, we have
).
Writing it this way, we have
| (6.57) | |||
where
![]() .
.
Returning back now to our two solutions (equations 6.51 and
6.52) we can combine them into one form by using step functions,
![]() , to give
, to give
| (6.58) |
Using the normalized plane-wave solutions (equation 4.21), we can write
| (6.59) |
The progagator now consists of a term (first term) propagating positive-energy solutions and another term (second term) propagating negative-energy solutions. The step functions ensure that the positive-energy solutions are propagated forward in time and the negative-energy solutions backward in time.
When propagating waves in the Klein-Gordon theory, the operator
![]() is sandwiched between the
propagator and the wave function to allow the orthogonality and
normalization conditions (equations 4.58 and 4.59,
respectively) to be used.
is sandwiched between the
propagator and the wave function to allow the orthogonality and
normalization conditions (equations 4.58 and 4.59,
respectively) to be used.
Consider a general wave,
| (6.60) |
consisting of positive- and negative-energy components. Propagating the positive-energy component gives
| (6.61) |
Using the orthonormal relationships (equations 4.58 and 4.59) give
Similar for the negative-energy component,
Thus
![]() propagates only the positive-energy
part of a general wave function forward in time and the
negative-energy part backward in time, as required.
The occurrence of a relative minus sign between equations 6.62
and 6.63 results from the difference in the direction of
propagation in time.
propagates only the positive-energy
part of a general wave function forward in time and the
negative-energy part backward in time, as required.
The occurrence of a relative minus sign between equations 6.62
and 6.63 results from the difference in the direction of
propagation in time.