Klein Paradox for Spin-1/2 Particles

Consider the scattering of an electron of energy $E$ and momentum $p=p_z$ by the electrostatic step-potential of the form (figure 5.4)

$$e\phi = \left\{ \begin{array}{cl} V_0 & \textrm{for}\ z > 0 \\ 0 & \textrm{for}\ z < 0 \end{array} \right. .$$ (5.279)

Figure 5.4: Electrostatic potential idealised with a sharp boundary, with an incident free-electron wave of energy $E$ moving to the right in region I.

For a free electron, we have $(E/c)^2=p^2+m^2c^2$, whereas in the presence of the constant potential

$$\left(\frac{E-V_0}{c}\right)^2 = (p^\prime)^2 + m^2c^2 ,$$ (5.280)

where $p^\prime$ is the momentum of the particle inside the potential.

The Dirac equation for $z<0$ is

$$(c\alpha\hat{p} + \beta mc^2)\psi = E\psi ,$$ (5.281)

while for $z>0$ we have

$$(c\alpha\hat{p} + \beta mc^2)\psi = (E-V_0)\psi ,$$ (5.282)

where it is understood that $\alpha=\alpha_3$ and $\hat{p} = \hat{p}_z$.

The incident wave in region I is

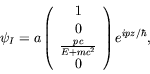$$\psi_I = a \left(\begin{array}{c} 1 \\ 0 \\ \frac{pc}{E+mc^2} \\ 0 \end{array}\right) e^{ipz/\hbar} ,$$ (5.283)

with $pc = \sqrt{E^2 - m^2c^4}$. The reflected wave in region I is

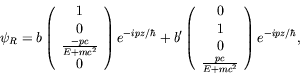$$\psi_R = b \left(\begin{array}{c} 1 \\ 0 \\ \frac{-pc}{E+mc^... ... \\ 0 \\ \frac{pc}{E+mc^2} \end{array}\right) e^{-ipz/\hbar} ,$$ (5.284)

The transmitted wave in region II is

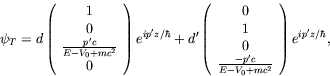$$\psi_T = d \left(\begin{array}{c} 1 \\ 0 \\ \frac{p^\prime c... ...ime c}{E-V_0+mc^2} \end{array}\right) e^{ip^\prime z/\hbar} ,$$ (5.285)

with $p^\prime c=\sqrt{(V_0-E)^2 - m^2c^4}$.

For now, we consider the case of $V_0>E+mc^2$ (strong field) for which the momentum $p^\prime$ is real and allows the free plane wave to propagate in region II. Continuity at the boundary requires $\psi_I + \psi_R = \psi_T$ and thus

$$a + b = d$$ (5.286)

$$b^\prime = d^\prime$$ (5.287)

$$\frac{pc}{E+mc^2}a - \frac{pc}{E+mc^2}b = \frac{-p^\prime c}{V_0-E-mc^2}d$$ (5.288)

$$\frac{pc}{E+mc^2}b^\prime = \frac{p^\prime c}{V_0-E-mc^2}d^\prime .$$ (5.289)

The equations for $b^\prime$ and $d^\prime$ can only be satisfied if $b^\prime = d^\prime = 0$. There is thus no spin flip of the electron at the boundary. Also

$$a-b = -\frac{p^\prime}{p}\frac{E+mc^2}{V_0-E-mc^2} d$$

$$= -\sqrt{\frac{(V_0-E+mc^2)(E+mc^2)}{(V_0-E-mc^2)(E-mc^2)}} d$$

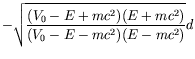$$\equiv -r d .$$ (5.290)

We thus have

$$a = \frac{d}{2}(1-r)$$

$$b = \frac{d}{2}(1+r)$$

$$\frac{b}{a} = \frac{1+r}{1-r}$$ (5.291)

$$\frac{d}{a} = \frac{2}{1-r} .$$ (5.292)

The particle current is given by

$$j(x) = c\psi^\dagger(x)\alpha_3\psi(x) .$$ (5.293)

We calculate

$$j_I = aa^* \frac{2pc^2}{E+mc^2} ,$$ (5.294)

$$j_R = -bb^* \frac{2pc^2}{E+mc^2} ,$$ (5.295)

$$j_T = -dd^* \frac{2p^\prime c^2}{V_0-E-mc^2} .$$ (5.296)

Since $r$ is real, the ratio of currents is

$$\frac{j_R}{j_I} = -\frac{bb^*}{aa^*} = -\frac{(1+r)^2}{(1-r)^2} ,$$ (5.297)

$$\frac{j_T}{j_I} = -\frac{p^\prime}{p} \frac{E+mc^2}{V_0-E-mc^2} \frac{dd^*}{aa^*}$$

$$= -\frac{4r}{(1-r)^2} .$$ (5.298)

Since $r>1$, we see that $\vert j_R\vert>\vert j_I\vert$. This result corresponds to the fact that the flow of $j_T$ is in the $-z$-direction, ie. the electrons are leaving region II, but according to our assumptions up to now, there are no electrons in there anyways. A reinterpretation is thus necessary.

To prevent the transition of all electrons to states of negative energy one has to require that all electron states $E<-mc^2$ are occupied with electrons. The potential $V_0>mc^2+E$ raises the electron energy in region II sufficiently for there to be an overlap between the negative continuum for $z>0$ and the positive continuum for $z<0$, as shown in figure 5.5. In the case of $V_0>E+mc^2$ the electrons striking the potential barrier from the left are able to knock additional electrons out of the vacuum on the right, leading to positron current flowing from left to right in the potential region. It is possible to understand the sign of $j_T$ by assuming that the electrons entering region I are coming from the negative continuum.

Figure 5.5: Klein Paradox interpretation using hole theory.

$$j_I + j_R = j_I\left( 1 -\frac{(1+r)^2}{(1-r)^2} \right) = -\frac{4r}{(1-r)^2}j_I = j_T .$$ (5.299)

Since the holes remaining in region II are interpreted as positrons, the phenomena can be understood as electron-positron pair creation at the potential barrier and is related to the decay of the vacuum in the presence of a strong field.