Free-Particle Solutions and Wave Packets

Because of the completeness of plane-wave solutions, we may superimpose plane waves to construct localized wave packets. The wave packets are also solutions to the Dirac equation since it is linear.

A positive-energy wave packet solution can be written as

$$\psi^{(+)}(\vec{x},t) = \int \frac{d^3p}{(2\pi\hbar)^{3/2}} ... ...ac{mc^2}{E}} \sum_{\pm s} b(p,s) u(p,s) e^{-ip\cdot x/\hbar} ,$$ (5.269)

where $b(p,s)$ is a complex scaler function. Normalized to unit probability gives

$$\int d^3x{\psi^{(+)}}^\dagger(\vec{x},t)\psi^{(+)}(\vec{x},t)$$

$$= \int\frac{d^3xd^3pd^3p^\prime}{(2\pi\hbar)^3} \sqrt{\frac{m^2c^4}... ...rime,s^\prime)u^\dagger(p,s)u(p^\prime,s^\prime) e^{i(p-p^\prime)\cdot x/\hbar}$$

$$= \int d^3p \frac{mc^2}{E} \sum_{\pm s,\pm s^\prime} b^*(p,s)b(p,s^\prime)u^\dagger(p,s)u(p,s^\prime)$$

$$= \int d^3p \frac{mc^2}{E} \sum_{\pm s,\pm s^\prime} b^*(p,s)b(p,s^\prime)\frac{E}{mc^2}\delta_{ss^\prime}$$

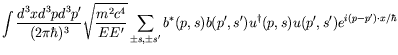$$= \int d^3p \sum_{\pm s} \vert b(p,s)\vert^2 = 1 .$$ (5.270)

The average current for such a wave packet is given by the expectation value of the velocity operator

$$\vec{j}^{(+)} = \int d^3x \psi^{(+)^\dagger} c\vec{\alpha} \psi^{(+)} = \int d^3x \overline{\psi}^{(+)} c\vec{\gamma} \psi^{(+)}$$

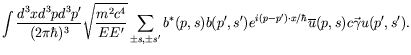$$= \int\frac{d^3xd^3pd^3p^\prime}{(2\pi\hbar)^3} \sqrt{\frac{m^2c^4}... ...-p^\prime)\cdot x/\hbar} \overline{u}(p,s) c\vec{\gamma} u(p^\prime,s^\prime) .$$ (5.271)

The space part of the Gordon decomposition

$$c\overline{\psi}_2\gamma^\mu\psi_1 = \frac{1}{2m} [\overline... ...c{i}{2m} \hat{p}_\nu (\overline{\psi}_2\sigma^{\mu\nu}\psi_1)$$ (5.272)

can be used. The Gordon decomposition decomposes the Dirac current density into a convection current-density term, similar to the nonrelativistic case, and an additional spin current-density term. We can now write

$$j_k^{(+)} = \int\frac{d^3xd^3pd^3p^\prime}{(2\pi\hbar)^3} \sqrt{\frac{m^2c^4}... ...\pm s,\pm s^\prime} b^*(p,s)b(p^\prime,s^\prime) e^{i(p-p^\prime)\cdot x/\hbar}$$

$$\cdot \overline{u}(p,s) \frac{1}{2m} \left[ (p_k + p_k^\prime) + \sigma_k^{\ \nu} (p_\nu - p_\nu^\prime) \right] u(p^\prime,s^\prime)$$

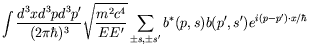$$\vec{j}^{(+)} = \int d^3p \frac{\vec{p}c^2}{E} \sum_{\pm s} \vert b(p,s)\vert^2 .$$ (5.273)

Using the normalization condition, the current can be written

$$\vec{j}^{(+)} = \langle c\vec{\alpha} \rangle_+ = \left\langle \frac{c^2\vec{p}}{E} \right\rangle .$$ (5.274)

Thus the average current for an arbitrary packet formed of positive energy solutions is just the classical group velocity. In the Schrödinger theory the velocity operator $\hat{v}=\hat{p}/m$ is proportional to the momentum, but this is not the case in the Dirac theory. In the Dirac theory the velocity operator for a free particle $c\hat{\alpha}$ is no longer a constant. We see that wave packets consisting of plane waves with only positive energy have the expectation value of the velocity $\vert\langle c\hat{\alpha}\rangle\vert \sim \vert\langle c^2\vec{p}/E \rangle\vert < c$, whereas the eigenvalues of $c\hat{\alpha}$ are exactly $\pm c$. This motivates us to consider a wave packet containing both positive and negative energy solutions:

$$\psi(\vec{x},t) = \int \frac{d^3p}{(2\pi\hbar)^{3/2}} \sqrt{... ...^{-ip\cdot x/\hbar} + d^*(p,s) v(p,s) e^{+ip\cdot x/\hbar} ] ,$$ (5.275)

where $b(p,s)$ and $d^*(p,s)$ are complex scalar functions. Normalized to unit probability, we have

$$\int d^3x \psi^\dagger(\vec{x},t) \psi(\vec{x},t)$$

$$= \int \frac{d^3xd^3pd^3p^\prime}{(2\pi\hbar)^{3}} \sqrt{\frac{m^2c... ...ime) u^\dagger(p,s) u(p^\prime,s^\prime) e^{i(p-p^\prime)\cdot x/\hbar} \right.$$

$$+ b^*(p,s) d^*(p^\prime,s^\prime) u^\dagger(p,s) v(p^\prime,s^\prime) e^{-i(p+p^\prime)\cdot x/\hbar}$$

$$+ d(p,s) b(p^\prime,s^\prime) v^\dagger(p,s) u(p^\prime,s^\prime) e^{i(p+p^\prime)\cdot x/\hbar}$$

$$+ \left. d(p,s) d^*(p^\prime,s^\prime) v^\dagger(p,s) v(p^\prime,s^\prime) e^{-i(p-p^\prime)\cdot x/\hbar} \right]$$

$$= \int d^3p \frac{mc^2}{E} \sum_{\pm s,\pm s^\prime} \left[ b^*(p,s) b(p,s^\prime) u^\dagger(p,s) u(p,s^\prime) \right.$$

$$+ b^*(p,s) d^*(-p,s^\prime) u^\dagger(p,s) v(-p,s^\prime) e^{-2ip_0 x_0/\hbar}$$

$$+ d(p,s) b(-p,s^\prime) v^\dagger(p,s) u(-p,s^\prime) e^{2ip_0 x_0/\hbar}$$

$$+ \left. d(p,s) d^*(p,s^\prime) v^\dagger(p,s) v(p,s^\prime) \right]$$

$$= \int d^3p \frac{mc^2}{E} \sum_{\pm s,\pm s^\prime} \left[ b^*(p,s... ..._{ss^\prime} + d(p,s) d^*(p,s^\prime) \frac{E}{mc^2} \delta_{ss^\prime} \right]$$

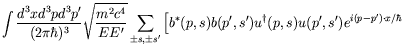$$= \int d^3p \sum_{\pm s} \left[ \vert b(p,s)\vert^2 + \vert d(p,s)\vert^2 \right] = 1 .$$ (5.276)

A short calculation shows the current of the wave packet is

$$j^k = \int d^3x \psi^\dagger(\vec{x},t) c\hat{\alpha}_k \psi(\vec{x},t)$$

$$= \int d^3p \left\{ \sum_{\pm s} \left[ \vert b(p,s)\vert^2 + \vert d(p,s)\vert^2 \right] \frac{p^kc^2}{E} \right.$$

$$+ ic \sum_{\pm s,\pm s^\prime} b^*(-p,s)d^*(p,s^\prime) e^{2ix_0p_0/\hbar} \overline{u}(-p,s) \sigma^{k0} v(p,s^\prime)$$

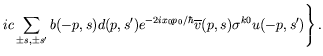$$- \left. ic \sum_{\pm s,\pm s^\prime} b(-p,s)d(p,s^\prime) e^{-2ix_0p_0/\hbar} \overline{v}(p,s) \sigma^{k0} u(-p,s^\prime) \right\} .$$ (5.277)

The first term represents the time-independent group velocity that appeared before for positive energy only wave packets. The second and third terms are interferences of the solutions with positive and negative energy, which oscillate time-dependently because of the factors $\exp(\pm 2ip_0x_0/\hbar)$. The frequency of this Zitterbewegung is

$$\frac{2p_0c}{\hbar} > \frac{2mc^2}{\hbar} \approx 2\times 10^{21} \textrm{s}^{-1} .$$ (5.278)