Use the Dirac equation to show that these wavefunctions differ from the ones normalized via
by a factor of ![]() .
.
for a general Lorentz transformation, where ![]() is a
is a ![]() matrix
which is a function of the parameters of the Lorentz transformation
and operates upon the four components of the column vector of the
wavefunction satisfying the Dirac equation.
matrix
which is a function of the parameters of the Lorentz transformation
and operates upon the four components of the column vector of the
wavefunction satisfying the Dirac equation.
- Suppose
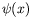 is the Dirac wavefunction in a frame
is the Dirac wavefunction in a frame 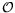 .
What is the wavefunction
.
What is the wavefunction
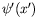 in a frame
in a frame
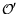 which is obtained from
which is obtained from 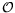 by a rotation
about the
by a rotation
about the 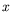 -axis through
-axis through 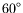 ?
?
- If a spin one-half particle at rest has its spin in the
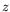 -direction, what is the probability that its spin will be observed
to be in a direction
-direction, what is the probability that its spin will be observed
to be in a direction 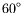 from the
from the 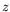 -axis.
-axis.
- Consider a Lorentz transformation to a frame moving in the
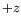 -direction with speed
-direction with speed 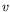 .
Obtain the transformation matrix
.
Obtain the transformation matrix 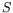 .
.
- Use the results of part (c) to get the wavefunction of a spin
one-half particle whose spin is in the
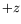 -direction and whose
velocity is
-direction and whose
velocity is 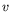 in the
in the 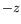 -direction.
Assume the wavefunction in the reset frame is
-direction.
Assume the wavefunction in the reset frame is 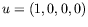 and apply
the boost of part (c).
and apply
the boost of part (c).
- Obtain the transformation matrix for the boost of part (c) followed by the rotation of part (a).
- In this new frame in which the particle has negative helicity and
a velocity
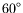 from the
from the 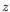 -axis, calculate the probability
that it will be observed to have its spin in the new
-axis, calculate the probability
that it will be observed to have its spin in the new 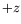 -direction.
-direction.
are projection operators which are said to identify states of definite chirality (handedness).
- Show that
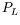 ,
, 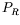 are legitimate projection operators in
that
are legitimate projection operators in
that
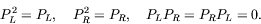
- Demonstrate that in the limit of high energy
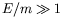 - or
equivalently in the massless limit - that the Dirac spinors for
positive helicity (right-handed) and negative helicity (left-handed)
states of momentum
- or
equivalently in the massless limit - that the Dirac spinors for
positive helicity (right-handed) and negative helicity (left-handed)
states of momentum 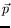 are given by
are given by
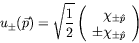
where
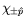 are spinors such that
are spinors such that
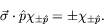
Note: In order to conveniently deal with massless particles, it is important to use the normalization
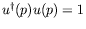 .
The appropriate Dirac spinors can then be found by multiplying the
usual forms by the factor
.
The appropriate Dirac spinors can then be found by multiplying the
usual forms by the factor 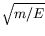 .
Demonstrate this.
.
Demonstrate this.
- Show that
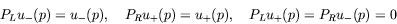
so that the chirality operator is equivalent to the helicity operator in this limit.
It expresses the Dirac current as the sum of a convection current similar to the nonrelativistic one, and a spin current.
for the general wave packet which contains both positive and negative energy plane waves.
Determine the wave packet at time ![]() developed from the above.
Consider the intensity of the negative energy solutions in the wave
packet.
What does one learn in general about the applicability of the
one-particle interpretation of the Dirac equation?
developed from the above.
Consider the intensity of the negative energy solutions in the wave
packet.
What does one learn in general about the applicability of the
one-particle interpretation of the Dirac equation?
involving the so-called anomalous magnetic moment.
(For the proton, of course, ![]() and for the neutron
and for the neutron ![]() .)
.)
- Verify that the choice
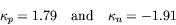
corresponds to the observed magnetic moments of these particles, and
- Show that the additional interaction disturbs neither the Lorentz covariance of the equation nor the hermiticity of the Hamiltonian.
- Show that this could be accommodated by modifying the Dirac equation
to become
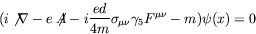
- Demonstrate that this equation is covariant but not invariant under a parity transformation.
which corresponds to an electric field of the form
Show that for ![]() there exists a finite probability of finding the
particle in a negative energy state if such negative energy states are
assumed to be originally empty.
In particular, work out quantitatively the two cases:
there exists a finite probability of finding the
particle in a negative energy state if such negative energy states are
assumed to be originally empty.
In particular, work out quantitatively the two cases: ![]() and
and
![]() and comment.
and comment.
and show that
Suggestion: Utilize normalized plane wave solutions of the Dirac equation
and simple first order perturbation theory
with
![]() as in the Klein-Gordon case.
as in the Klein-Gordon case.
- Verify that this is so for the current:
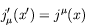
and also
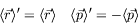
- Repeat these calculations for the charge-conjugation
transformation
 .
In particular, show
.
In particular, show
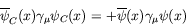
and interpret using the hole theory.
-
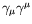 ,
,
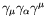 ,
,
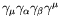
- Simplify
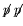 ,
,
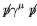 ,
,
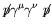 .
.
- Find the energy levels.
- Solve the problem of scattering of such an electron with momentum
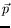 off this potential.
off this potential.
where ![]() is the electron spinor.
That is, show that in the extreme relativistic limit, the chirality
operator (
is the electron spinor.
That is, show that in the extreme relativistic limit, the chirality
operator (![]() ) is equal to the helicity operator; and so, for
example,
) is equal to the helicity operator; and so, for
example,
![]() corresponds to an electron of negative helicity.
corresponds to an electron of negative helicity.