MATH 144: Calculus for the Physical Sciences I

Concept 3.4.1. Limit laws.

Assume that \(\displaystyle \lim_{x \to a} f(x)\) and \(\displaystyle \lim_{x \to a} g(x)\) exist. Then:

• Limit of a constant: \(\displaystyle \lim_{x \to a} c = c\) for any \(c \in \mathbb{R}\text{.}\)
• Limit of \(x\text{:}\) \(\displaystyle \lim_{x \to a} x = a\text{.}\)
• Sum rule: \(\displaystyle \lim_{x \to a} (f(x) \pm g(x)) = \lim_{x \to a} f(x) \pm \lim_{x \to a} g(x)\text{.}\)
• Product rule: \(\displaystyle \lim_{x \to a} \left( f(x) \cdot g(x) \right) = \left( \lim_{x \to a} f(x) \right) \left( \lim_{x \to a} g(x) \right).\)
• Quotient rule: \(\displaystyle \lim_{x \to a} \frac{f(x)}{g(x)} = \frac{\underset{x \to a}{\text{lim}}f(x)}{\underset{x \to a}{\text{lim}} g(x)}\) if \(\displaystyle \lim_{x \to a} g(x) \neq 0\text{.}\)
• Root rule: \(\displaystyle \lim_{x \to a} \left( f(x) \right)^{1/n} = \left( \lim_{x \to a} f(x) \right)^{1/n}\text{,}\) where \(n\) is a positive integer. For \(n\) even we require that \(\displaystyle \lim_{x \to a} f(x) >0\) so that the root is real and the limit is well defined.

Concept 3.4.2. Simplifying a function.

If \(f(x) = g(x)\) for \(x \neq a\text{,}\) then

provided the limits exist. In practice, what this means is that when you are evaluating \(\displaystyle \lim_{x \to a} f(x)\text{,}\) then you can manipulate \(f(x)\) by simplifying it using things like factorization, rationalization, common denominator, etc., assuming that \(x \neq a\text{,}\) and it will not change the limit.

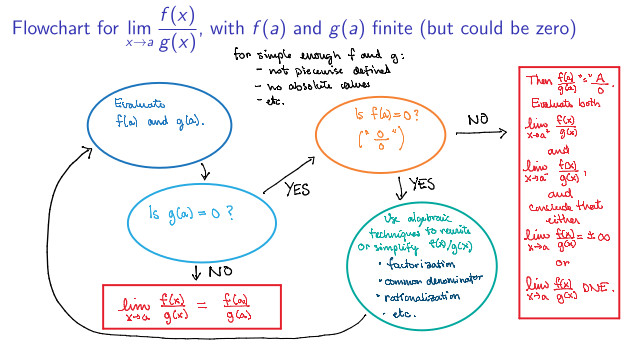
Concept 3.4.3. Flowchart.

This flowchart is for calculating the limit

for simple enough functions \(f(x)\) and \(g(x)\) (not piecewise-defined, no absolute values, etc.) such that both \(f(a)\) and \(g(a)\) are finite. This is the form of many functions that we will encounter for the time being. If your function is not of this form, you may first need to use algebraic techniques, such as common denominator, to transform it into this form.

Concept 3.4.5. Squeeze theorem.

First, if \(f(x)\leq g(x)\) for all \(x\) near \(a\) (except possibly at \(x=a\)), and if the limits of both functions exist as \(x\) approaches \(a\text{,}\) then

The Squeeze theorem states that, if \(g(x)\leq f(x)\leq h(x)\) for all \(x\) near \(a\) (except possibly at \(x=a\)), and if