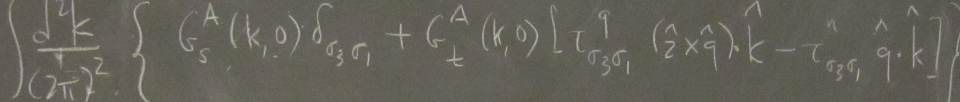
I am interested in a variety of problems in theoretical condensed matter physics. My main focus is the emergence of novel phenomena in many-particle systems subject to the laws of quantum mechanics. Current areas of research include topological phases of matter, strongly correlated electrons, quantum transport in low-dimensional systems, and connections between condensed matter physics and high-energy physics.
Please see below for short summaries of some recent research projects in which I have been involved.
Möbius molecules and fragile Mott insulators
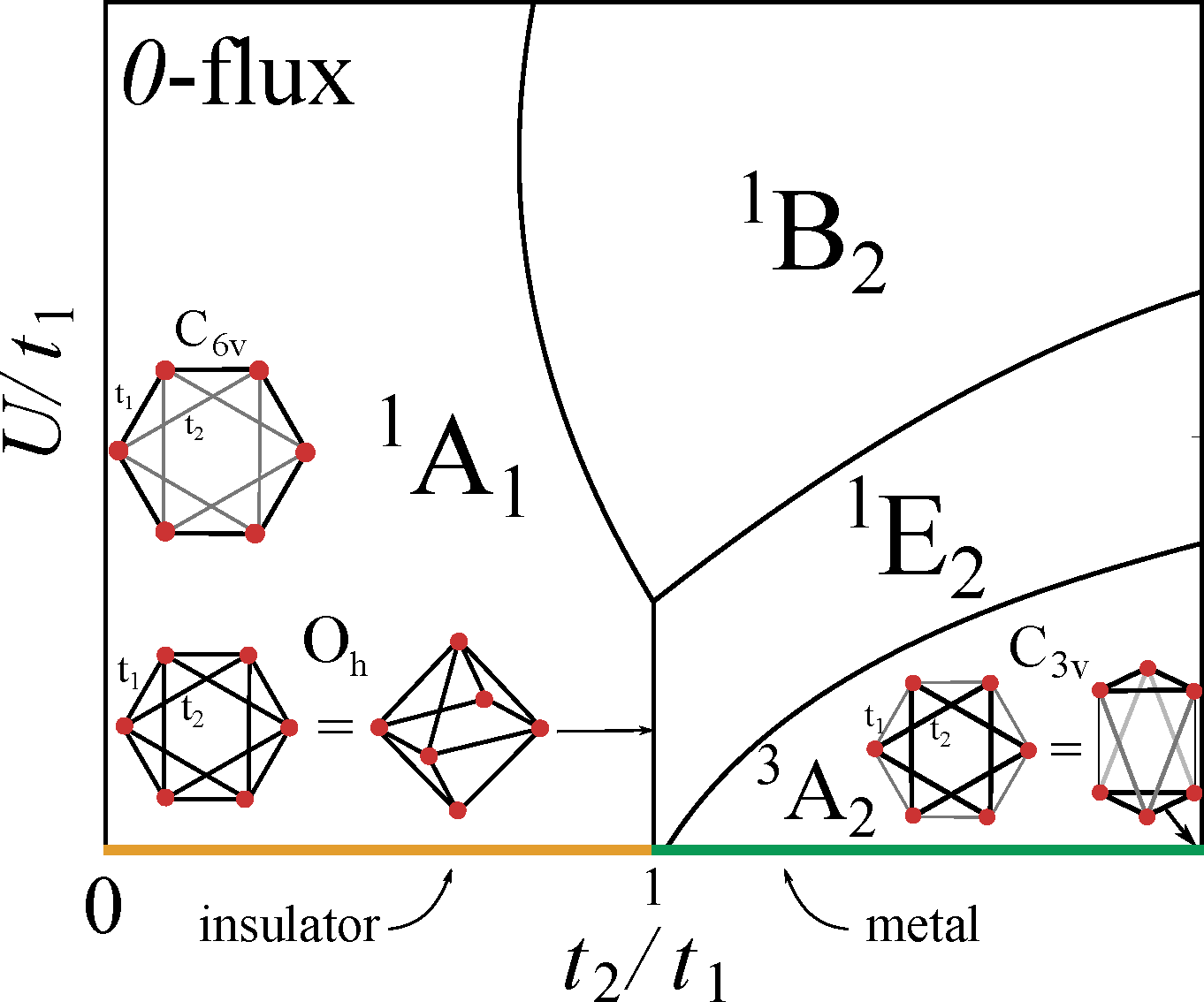Motivated by the concept of Möbius aromatics in organic chemistry, we extend the recently introduced concept of fragile Mott insulators (FMI) to ring-shaped molecules with repulsive Hubbard interactions threaded by a half-quantum of magnetic flux (hc/2e). In this context, a FMI is the insulating ground state of a finite-size molecule that cannot be adiabatically connected to a single Slater determinant, i.e., to a band insulator, provided that time-reversal and lattice translation symmetries are preserved. Based on exact numerical diagonalization for finite Hubbard interaction strength U and existing Bethe-ansatz studies of the one-dimensional Hubbard model in the large-U limit, we establish a duality between Hubbard molecules with 4n and 4n+2 sites, with n integer. A molecule with 4n sites is an FMI in the absence of flux but becomes a band insulator in the presence of a half-quantum of flux, while a molecule with 4n+2 sites is a band insulator in the absence of flux but becomes an FMI in the presence of a half-quantum of flux. Including next-nearest-neighbor-hoppings gives rise to new FMI states that belong to multidimensional irreducible representations of the molecular point group, giving rise to a rich phase diagram.
For further reading:
L. Muechler, J. Maciejko, T. Neupert, and R. Car, arXiv:1409.6732.
Surface Majorana fermions and bulk collective modes in superfluid 3He-B
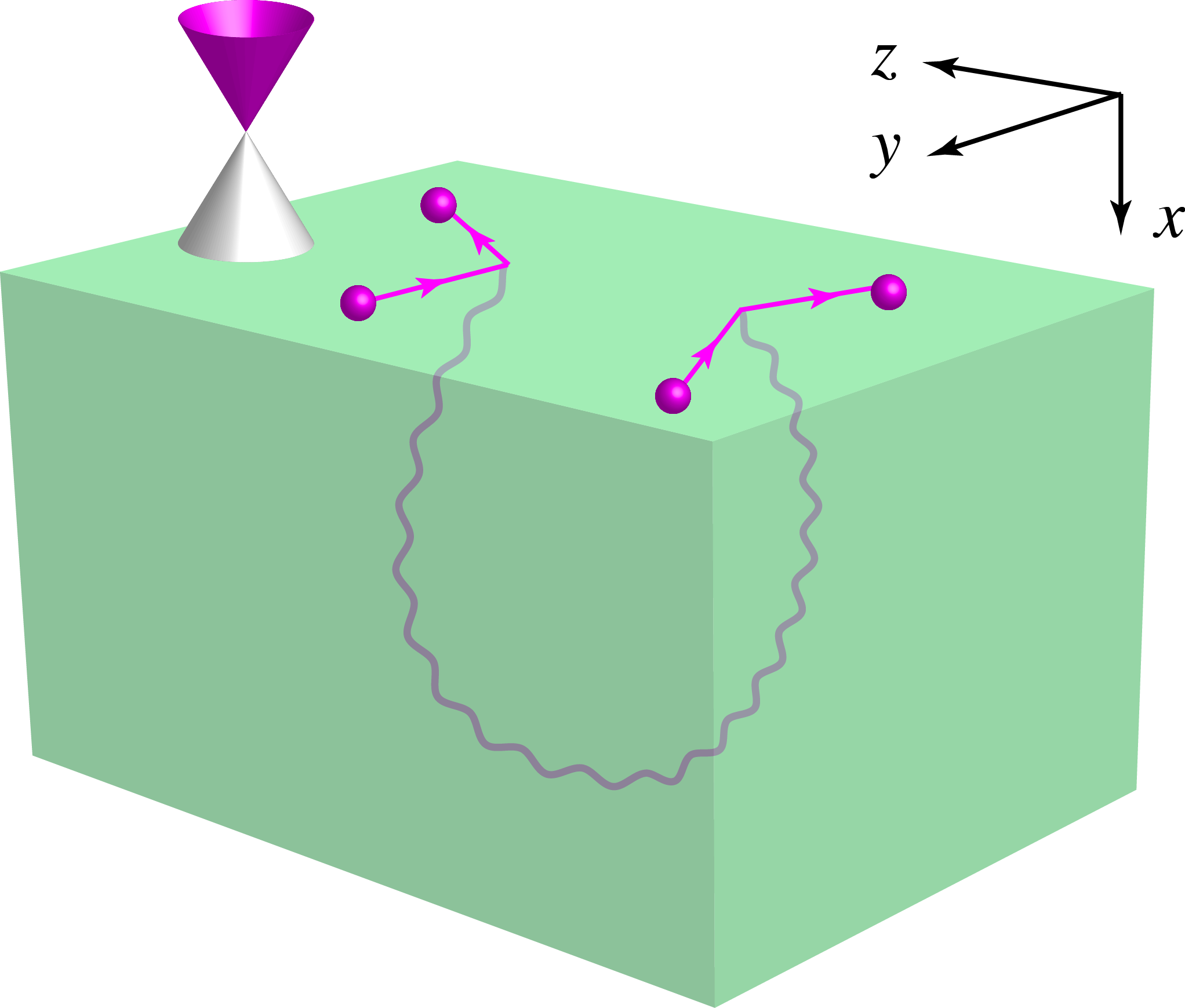The theoretical study of topological superfluids and superconductors has so far been carried out largely as a translation of the theory of noninteracting topological insulators into the superfluid language, whereby one replaces electrons by Bogoliubov quasiparticles and single-particle band Hamiltonians by Bogoliubov-de Gennes Hamiltonians. Band insulators and superfluids are, however, fundamentally different: while the former exist in the absence of inter-particle interactions, the latter are broken symmetry states that owe their very existence to such interactions. In particular, unlike the static energy gap of a band insulator, the gap in a superfluid is due to a dynamical order parameter that is subject to both thermal and quantum fluctuations. In this work, we explore the consequences of bulk quantum fluctuations of the order parameter in the B phase of superfluid 3He on the topologically protected Majorana surface states. Neglecting the high-energy amplitude modes, we find that one of the three spin-orbit Goldstone modes in 3He-B couples to the surface Majorana fermions. This coupling in turn induces an effective short-range two-body interaction between the Majorana fermions, with coupling constant inversely proportional to the strength of the nuclear dipole-dipole interaction in bulk 3He. A mean-field theory estimate of the value of this coupling suggests that the surface Majorana fermions in 3He-B are in the vicinity of a quantum phase transition to a gapped time-reversal symmetry breaking phase.
For further reading:
Y. J. Park, S. B. Chung, and J. Maciejko, arXiv:1409.3844.
Superconductivity of disordered Dirac fermions in graphene
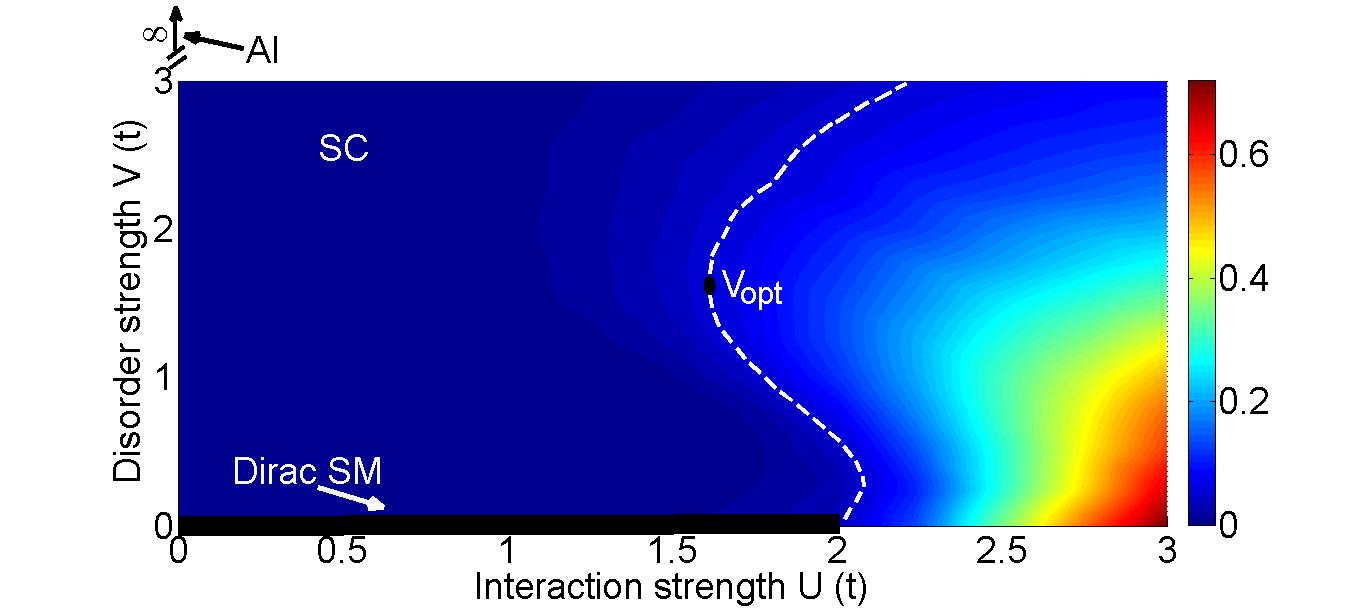We numerically study the interplay between superconductivity and disorder on the graphene honeycomb lattice with on-site Hubbard attractive interactions U using a spatially inhomogeneous self-consistent Bogoliubov-de Gennes (BdG) approach. In the absence of disorder there are two phases at charge neutrality. Below a critical value Uc for attractive interactions there is a Dirac semimetal phase and above it there is a superconducting phase. We add scalar potential disorder to the system, while remaining at charge neutrality on average. Numerical solution of the BdG equations suggests that while in the strong attraction regime (U > Uc) disorder has the usual effect of suppressing superconductivity, in the weak attraction regime (U < Uc) weak disorder enhances superconductivity. In the weak attraction regime, disorder that is too strong eventually suppresses superconductivity, i.e., there is an optimal disorder strength that maximizes the critical temperature Tc. Our numerical results also suggest that in the weakly disordered regime, mesoscopic inhomogeneities enhance superconductivity significantly more than what is predicted by a spatially uniform mean-field theory à la Abrikosov-Gorkov. In this regime, superconductivity consists of rare phase-coherent superconducting islands. We also study the enhancement of the superconducting proximity effect by disorder and mesoscopic inhomogeneities, and obtain typical spatial plots of the tunneling density of states and the superfluid susceptibility that can be directly compared to scanning tunneling miscroscopy (STM) experiments on proximity-induced superconductivity in graphene.
For further reading:
I. D. Potirniche, J. Maciejko, R. Nandkishore, and S. L. Sondhi, Phys. Rev. B 90, 094516 (2014).
Weyl semimetals with short-range interactions
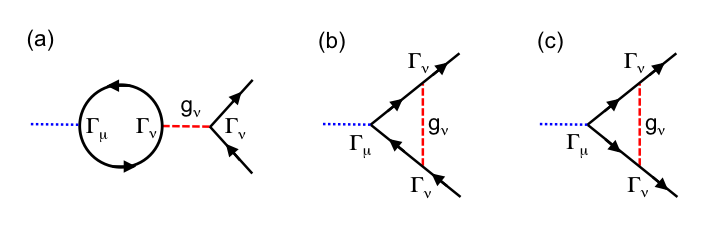We construct a low-energy effective field theory of fermions interacting via short-range interactions in a simple two-band model of a Weyl semimetal on the cubic lattice and investigate possible broken-symmetry ground states through a one-loop renormalization group (RG) analysis. Using the symmetries of the noninteracting Hamiltonian to constrain the form of the interaction term leads to four independent coupling constants. We investigate the stability of RG flows towards strong coupling and find a single stable trajectory. In order to explore possible broken-symmetry ground states, we calculate susceptibilities in the particle-hole and particle-particle channels along this trajectory and find that the leading instability is towards a fully gapped spin-density wave (SDW) ground state. The sliding mode of this SDW couples to the external electromagnetic fields like the Peccei-Quinn axion field of particle physics. We also study the maximally symmetric version of our model with a single independent coupling constant. Possible ground states in this case are either gapless ferromagnetic states where the spin waves couple to the Weyl fermions like the spatial components of a (possibly chiral) gauge field, or a fully gapped spin-singlet Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) superconducting state.
For further reading:
J. Maciejko and R. Nandkishore, Phys. Rev. B 90, 035126 (2014).
Topological order in a correlated three-dimensional topological insulator
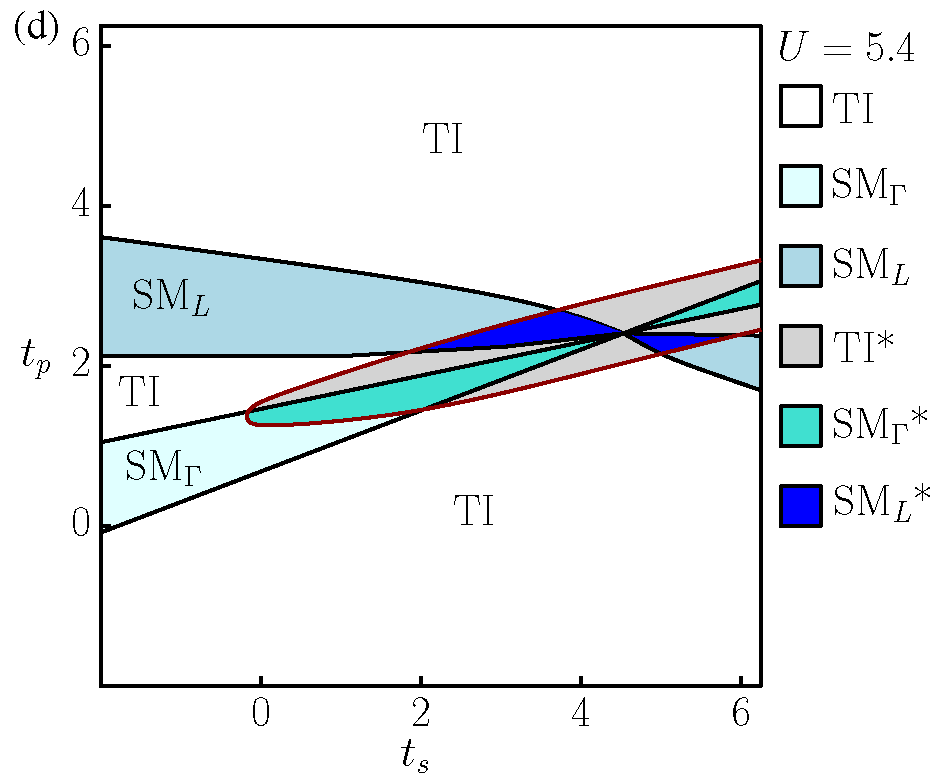Motivated by experimental progress in the growth of heavy transition metal oxides, we theoretically study a class of lattice models of interacting fermions with strong spin-orbit coupling. Focusing on interactions of intermediate strength, we derive a low-energy effective field theory for a fully gapped, topologically ordered, fractionalized state with an eight-fold ground-state degeneracy. This state is a fermionic symmetry-enriched topological phase with particle-number conservation and time-reversal symmetry. The topological terms in the effective field theory describe a quantized magnetoelectric response and nontrivial mutual braiding statistics of dynamical extended vortex loops with emergent fermions in the bulk. We explicitly compute the expected mutual statistics in a specific model on the pyrochlore lattice within a slave-particle mean-field theory. We argue that our model also provides a possible condensed-matter realization of oblique confinement.
For further reading:
J. Maciejko, V. Chua, and G. A. Fiete, Phys. Rev. Lett. 112, 016404 (2014).
Topological order in a correlated Chern insulator
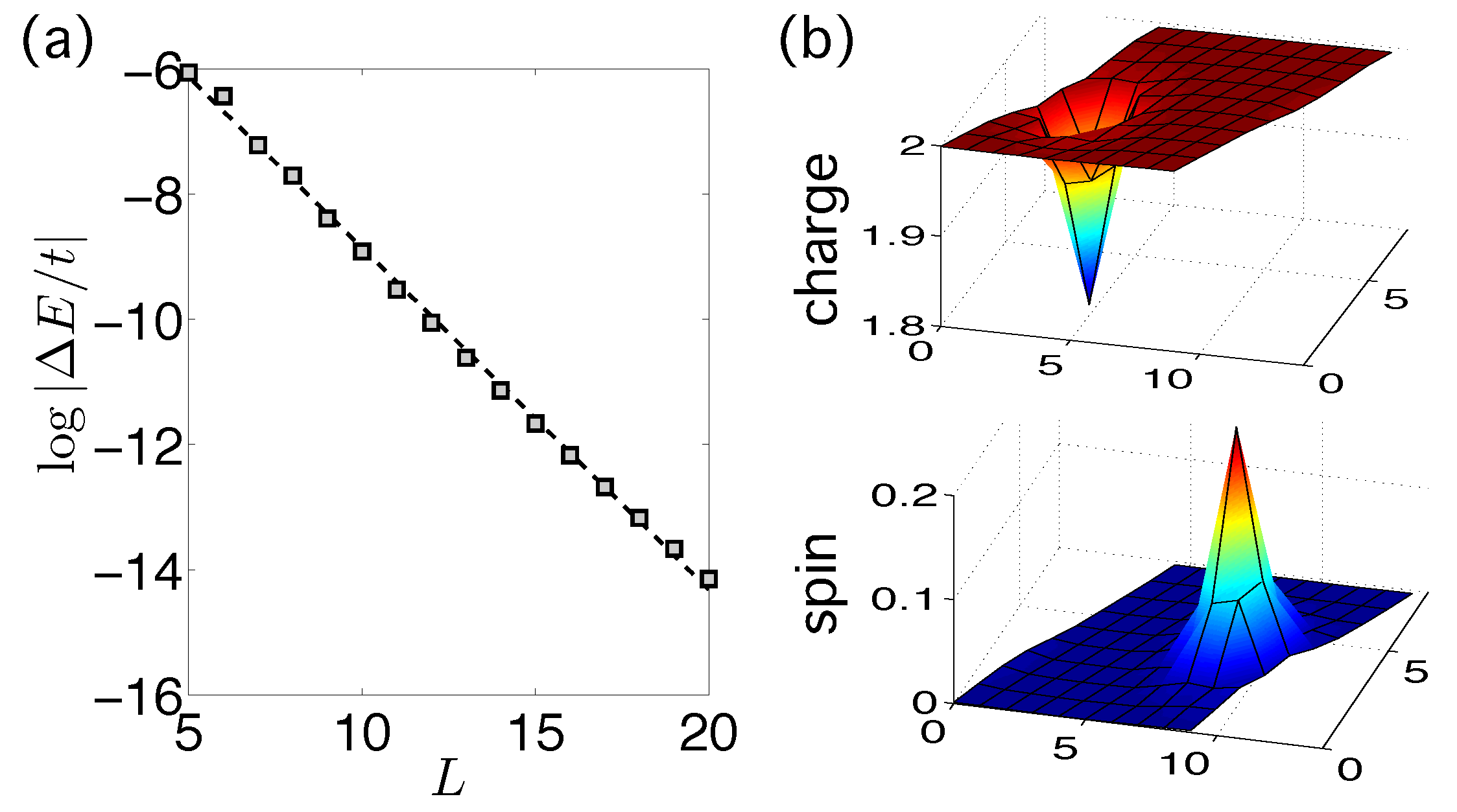We study the effect of electron-electron interactions in a spinful Chern insulator. For weak on-site repulsive interactions at half-filling, the system is a weakly correlated Chern insulator adiabatically connected to the noninteracting ground state, while in the limit of infinitely strong repulsion the system is described by an effective spin model recently predicted to exhibit a chiral spin liquid ground state. In the regime of large but finite repulsion, we find an exotic gapped phase with characteristics partaking of both the noninteracting Chern insulator and the chiral spin liquid. This phase has an integer quantized Hall conductivity 2e2/h and quasiparticles with electric charges that are integer multiples of the electron charge e, but the ground state on the torus is four-fold degenerate and quasiparticles have fractional statistics. We discuss how these unusual properties affect the outcome of a charge pumping experiment and, by deriving the topological field theory, elucidate that the topological order is of the exotic Z2 double-semion type.
For further reading:
J. Maciejko and A. Rüegg, Phys. Rev. B 88, 241101(R) (2013).