Section 3: The Syntax and Fixed Semantics of MIZAR MSE
These next sections define the syntax and fixed semantics of the
MIZAR Multisorted Predicate Calculus with Equality, abbreviated
MIZAR MSE.
3.1: Identifiers, Sorts, Constants, Variables, and Terms
One of the first issues that we must grapple with is the problem of
identifying the objects that we wish to talk about.
This can be done either directly or indirectly.
The direct way of identifying an object is to give it a name or an
object identifier.
The value or denotation of an object identifier is the object currently named
by the identifier.
The precise syntactic specification of an object identifier is given by the
following BNF grammar (for the notation see section 2.1):
| Identifier ::= | { IdentifierChar }+ { ' } |
| IdentifierChar ::= | A..Z | a..z | 0..9 | _ |
Thus 0, 0'', 1a2, aa', Hello and Good_bye are all syntactically correct object identifiers.
Instead of simply having objects of only one kind,
we divide the universe of discourse into disjoint collections called
sorts.
Sorts are given names, just like objects.
We often use only capital letters to name sorts.
So typically a sort will have an identifier like THING,
or OBJECT.
But we will also have sorts with names like Nat or Int.
Sometimes a particular name always refers to one specific object ---
as in the figure ``7'' that names the number seven.
In this case we say that the identifier ``7'' is a constant
(the identifier ``7'' has constant denotation).
But often, as in real life, the same name will refer to different
objects depending on the context in which it is used --- such as the name
Fred.
In this case we say the the identifier ``Fred'' is a variable
(the denotation of ``Fred'' is variable).
The use of the word ``variable'' is not meant to imply that the value of
the object identifier is fuzzy or undefined, only that it can change
depending on context.
The relationship between identifiers and objects in a logical system
is both analogous to and different from the relationships between
identifiers and objects in programming languages.
Some constant declarations are meant to apply to the entire proof.
These are called global constants, and have the syntax:
| GlobalConstantsDeclaration ::= | given QualifiedObjects |
For example the beginning of this MIZAR proof text
defines seven constants, three of sort INTEGER and four of
sort PERSON.
Such a declaration occurs only in the environment portion of an argument.
Unless these object identifiers are redeclared, their denotations
are fixed for the remainder of the proof.
environ
given 1,2,3 being INTEGER;
given Fred, Barney, Wilma, Pebbles being PERSON;
We can also refer to objects in the universe of discourse by the
indirect means of expressions involving other directly identified objects.
For example, the object identifier a directly refers to the
object named a, while 1+a is an expression that could refer to
the integer that is the successor of the integer named by a.
Expressions, including just an object identifier by itself, that result in
references to objects are called terms.
Each term is an expression that refers to exactly one object.
The MIZAR MSE logical system supports only simple terms syntactically consisting
of an object identifier.
This lets us ignore the various issues associated with expressions, such as
the meaning of the + operator on objects that are not numbers.
Thus the precise syntactic specification of a term is rather simple:
Each term refers to a specific object of a certain sort, and
in any given context, a term can belong to only one sort.
3.2: Predicates and Atomic Formulas
The most basic kind of statement that we can make about a thing
is that some fact does or does not hold for it.
For example suppose that A and B are two constants of some, unspecified,
sort:
``It is raining.''
``A is a knight.''
``A is taller than B.''
we can read these as, respectively,
The fact ``it is raining'' is true.
The ``knight'' characteristic holds for A.
The ``taller than'' relationship holds between A and B.
Observe that these statements are about things --- 0,1, or 2 things
in this case.
Each of these statements is an example of a predicate.
Each predicate has 0, 1, or more arguments, and the meaning of the
predicate depends on the things named by the arguments.
The predicate is true when the property holds among the given
arguments, and it is false when the property doesn't hold.
For example we might interpret the predicates Raining, Knight,
and Taller in the obvious way, and then apply them to the
objects A and B to obtain three sentences
Raining[]
Knight[A]
Taller[A, B]
which correspond in meaning to the three previous ones.
Note how the Raining predicate has no arguments, and so is
applied to the empty list [].
The number of arguments that a predicate has is called its arity.
We have special names for predicates with certain arities.
A predicate with one argument is a property.
When an object is fixed in some context, the object either has
the property or does not.
Properties are generally used to make statements about individuals.
A predicate with 2 or more arguments is a relation.
Given a number of objects in a context, and given a specific relation,
the relation either holds among the objects or it does not.
Relations are generally used to describe relationships among things.
We do not give a special name to a predicate with no arguments.
It is true or false, depending on the context in which it appears.
Such a predicate is generally used as an abbreviation for a more complex
statement about the world that we prefer not to repeatedly write in long
form.
The precise specification of the meaning of a predicate depends
in general on the specific interpretation being used.
For example less[A,B] could mean that object A is smaller
than object B, or that object B is smaller than object A.
Assigning meaning to the predicates is accomplished through the
interpretation.
However, we have two special predicates whose meaning never changes.
They are called equality and inequality.
For example A=B means A and B name the same thing,
while the formula A<>C means that A and C
name different things.
All of these simple statements are called atomic formulas.
Use of the term ``formula'' indicates that we are concerned with the
form of the statement, not its content.
The term ``atomic'' indicates that these objects are the
building blocks for more complex formulas.
Here is the BNF grammar for an atomic formula.
| AtomicFormula ::= | Equality |
Inequality |
PredicativeFormula |
contradiction |
| Inequality ::= | Term <> Term |
| PredicativeFormula ::= | PredicateId [ [ Term { , Term } ] ] |
The reserved word contradiction is a formula that is always false.
Observe that Knight, Raining, and Taller are all legal
predicate identifiers, and that Knight[], Knight[A], and
Knight[x,y] are all syntactically legal atomic formulas.
3.3: Logical Connectives and Compound Formulas
We can combine atomic formulas into more complex sentences using
the connectives & (read as ``and''), or, not and implies.
The syntactic rules for constructing sentences from these connectives are
given by the following BNF grammar.
| Formula ::= | AndOrFormula |
ConditionalFormula |
BiconditionalFormula |
QuantifiedFormula |
| AndOrFormula ::= | ConjunctiveFormula |
DisjunctiveFormula |
| DisjunctiveFormula ::= | ConjunctiveFormula { or ConjunctiveFormula } |
| ConjunctiveFormula ::= | UnitFormula { & UnitFormula } |
| UnitFormula ::= | { not } ( AtomicFormula | () Formula ) |
| ConditionalFormula ::= | AndOrFormula implies AndOrFormula |
| BiconditionalFormula ::= | AndOrFormula iff AndOrFormula |
(Quantified formulas are discussed in section 3.5.)
Note that some connectives are treated in different productions with
slightly different forms.
This is because we assign a different precedence to each of the
operators in order to save us from writing one pair of parentheses for
each connective.
The precedence of the operators, in decreasing order is:
not
&
or
implies, iff
A convenient rule of thumb for remembering the precedence of the operators is
to correspond not with unary minus, & with ×, and or
with + in the usual arithmetic expressions.
The logical connectives & and or are associative just like
× and +.
Putting parentheses (()) around a subformula has the usual effect of
making the enclosed subformula into a single unit with respect to
the remainder of the enclosing formula.
The operators implies and iff have equal priority, but they are not
associative.
This fortunately does not create a problem of ambiguity because the
grammar ensures that implies and iff can appear only between
subformulas that do not contain unparenthesized implies and iff
operators.
In brief, MIZAR logical formulas are evaluated in the same way that
logical expressions in Pascal or C are evaluated.
The grammar tells us how to construct complex sentences from existing ones.
We give them meaning by showing how to obtain the truth of the complex
sentence from the meaning of its individual parts.
Let  and
and  stand for arbitrary MIZAR sentences,
except that we assume that the sentences are enclosed in ().
This avoids some technical difficulties caused by operators having
unequal precedence.
(Consider the case of placing an & between the formulas
P[] or Q[] and R[] or S[].
If we did not enclose each formula in parentheses, placing an &
between them would result in the formula
P[] or Q[] & R[] or S[] instead of our intended
one of (P[] or Q[]) & (R[] or S[]).
Users of macro processors are familiar with this problem.)
stand for arbitrary MIZAR sentences,
except that we assume that the sentences are enclosed in ().
This avoids some technical difficulties caused by operators having
unequal precedence.
(Consider the case of placing an & between the formulas
P[] or Q[] and R[] or S[].
If we did not enclose each formula in parentheses, placing an &
between them would result in the formula
P[] or Q[] & R[] or S[] instead of our intended
one of (P[] or Q[]) & (R[] or S[]).
Users of macro processors are familiar with this problem.)
The simplest connective is not, and not  is true if
is true if  is
false, and false if
is
false, and false if  is true.
We can express this using a truth-table.
is true.
We can express this using a truth-table.
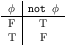
The remaining connectives take two arguments, and are defined by
the following truth-table.
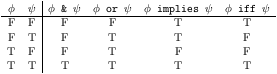
Note how & is true exactly when both propositions are true, and or is
true when at least one proposition is true.
This property lets us avoid having to put parentheses about the subformulas
in a conjunctive or disjunctive formula.
Thus (P[] & Q[]) & R[] is the same as P[] & (Q[] & R[]),
and (P[] or Q[]) or R[] is the same as P[] or (Q[] or R[]).
Here are some examples of some simple sentences:
not Knight[A] & Knight[B]
This can be read as ``A is not a knight, and B is a knight''.
This sentence
Knave[A] & (Raining[] or Knight [B])
can be read as ``A is a knave, and it is raining or B is a knight''.
Note how we use parentheses to override the basic precedence of the
connectives.
For example the next sentence has a different meaning from the previous
one
Knave[A] & Raining[] or Knight[B]
but is the same as
(Knave[A] & Raining[]) or Knight[B]
How do we determine the truth value of a complex sentence?
If we know the truth value of the atomic formulas in a complex
sentence, then we can determine the truth value of the complex
sentence by simply building up successively more complex subsentences ---
just as we do for arithmetic expressions.
Here are some examples.
The sentence
A=B & not A=C or A=C & not A=B or B=C & not A=B
is true when exactly two of A, B, C are equal.
It is false otherwise.
Suppose that we have A=1, B=2, C=1.
How do we determine the truth value of this formula under this interpretation?
First we break it into its three conjunctive subformulas:
A=B & not A=C
A=C & not A=B
B=C & not A=B
Since the subformulas are connected together by or to form the main
formula, the main formula will be true if at least one of its
subformulas is true.
Next we break each conjunctive formula into its unit formulas.
For the first subformula this is
A=B
not A=C
This subformula will be true if both of its sub-subformulas are true.
From the values of A, B, C given above we see that
A=B is false; and A=C is true, so not A=C is false.
Either one of the sub-subformulas being false is enough to make
the subformula false.
Thus far we cannot make any conclusions about the truth value of the
main formula.
However, the second conjunctive subformula A=C & not A=B
is true, and this makes the main formula true.
Thus we have that the main formula is true under the interpretation
A=1, B=2, C=1.
We can also perform this process on the parse tree for the formula,
and simply assign a logical value to each node.
This process can be represented diagrammatically as follows under
the interpretation A=1, B=2, C=1.
A=B & not A=C or A=C & not A=B or B=C & not A=B
--- --- --- --- --- ---
F T T F F F
------- ------- -------
F T T
------------- ------------- -------------
F T F
-----------------------------------------------
T
For our next example, suppose that we have three predicates Odd, Even, and
Divides which we interpret as follows:
- Odd[x] -- is true exactly when x is an odd integer.
- Even[x] -- is true exactly when x is an even integer.
- Divides[x,y] -- is true exactly when x divides into y
leaving no remainder.
Under this interpretation we have:
Odd[1] is true, Even[1] is false, Odd[2] is false, Even[2] is true
Divides[2,4] is true, Divides[2,5] is false, Divides[2,1] is false
Now suppose x=3 and y=7.
What is its truth value of this sentence?
(Odd[x] or Even[x]) & not(Even[x] & Odd[x]) or not Divides[x,y]
------ ------- ------- ------ ------------
T F F T F
------------------- ------------------ ----------------
T F T
---------------------
T
-------------------------------------------
T
---------------------------------------------------------------
T
In the case x=4 and y=8 the sentence is also true.
3.4: Conditionals and Biconditionals
One of the more striking aspects of an argument is the frequent repetition of a phrase ``If . . . then . . .''.
For example, ``If Fred is a herring then Fred is a fish''.
This kind of sentence is called a conditional() because it states that
a conditional relationship holds between the antecedent
(following the ``if'') and the consequent (following the ``then'').
If the antecedent is true then the consequent is also true.
All formulas of the form  implies
implies  are conditionals.
They can also be read as ``if
are conditionals.
They can also be read as ``if  then
then  ''.
Think of the sentence
''.
Think of the sentence  implies
implies  in the following
way.
If
in the following
way.
If  implies
implies  is true, and we also know that
is true, and we also know that
 is true, then we can conclude that
is true, then we can conclude that  is also true.
This is a direct consequence of the definition of the implication
connective.
Here is an example of how conditionals are used in an argument:
is also true.
This is a direct consequence of the definition of the implication
connective.
Here is an example of how conditionals are used in an argument:
Suppose that
Knight[A],
Knight[A] implies Knave[B], and
Knave[B] implies Knight[C]
are all true. Then from the first two we can conclude that Knave[B] is true. From the third, since Knave[B] is true we can conclude that Knight[C] is true.
The implies connective can be expressed in terms of not and or.
Specifically,  implies
implies  is equivalent to
not
is equivalent to
not  or
or  .
You can check to see that these two sentences have exactly the same truth-table.
Remember this equivalence!
.
You can check to see that these two sentences have exactly the same truth-table.
Remember this equivalence!
A biconditional is the combination of two conditionals.
The biconditional  iff
iff  , read
``
, read
`` if and only if
if and only if  '', or
``
'', or
`` is equivalent to
is equivalent to  '', simply means
(
'', simply means
( implies
implies  ) & (
) & ( implies
implies  ).
).
The ability to transform formulas into equivalent ones is important,
and you should make an attempt to become
thoroughly familiar with the various techniques that we introduce.
3.5: Quantifiers
In English, we often say things like:
``All mammals have hair.''
``Some mammals have four legs.''
These sentences state facts, not about some specific individual, but
about classes of individuals.
We can interpret the first sentence as saying that no matter what mammal
you pick, it will always have hair.
This is an example of a universal statement.
The property of having hair applies universally to the class of things
we call mammals.
The second sentence can be interpreted as saying that at least one of the
members of the class of mammals has four legs.
Possibly more, or even all of the members of the class do.
This is an example of an existential statement, so called, because
it asserts the existence of at least one thing satisfying the
stated property.
In MIZAR, we would translate these two sentences as something like:
for x being MAMMAL holds HasHair[x]
ex x being MAMMAL st FourLegs[x]
under the obvious interpretation of the predicates HasHair
and FourLegs.
The phrases for x being MAMMAL holds and ex x being MAMMAL st
are called quantifications.
The keyword for is called the universal quantifier, and the
keyword ex is called the existential quantifier.
Each quantifier applies to the syntactically complete formula that follows
the holds or st.
In a quantified formula, some object identifiers are associated with a quantifier,
while others are not.
Those associated with a quantifier are called bound, and the relationship
between the object identifier and its associated quantifier is called
the binding of the object identifier.
Object identifiers not associated with a quantifier are called free.
The notions of bound and free occur with respect to a particular formula.
An object identifier that is free in one formula may be bound in another
formula.
(Note that in usual logical parlance the word ``variable'' is used in
a sense similar to the way we use ``object identifier''.)
3.6: Scope and Binding
It is important to be able to determine the bindings of the object
identifiers in a formula to the quantifiers in the formula.
This is done by determining the scope of each quantifier.
When a quantifier introduces an object identifier, then every occurrence
of the object identifier inside the scope of the quantifier is bound
to the quantifier.
The scope of each quantifier is determined according to the following rules.
-
Suppose that
 is a formula with no quantifiers.
Then every occurrence of every object identifier in
is a formula with no quantifiers.
Then every occurrence of every object identifier in  is free.
is free.
-
Any free object identifiers in
 and
and  are still free in, and any bound
identifiers retain their bindings in, all of the following formulas
not
are still free in, and any bound
identifiers retain their bindings in, all of the following formulas
not 
 &
& 
 or
or 
 implies
implies 
 iff
iff 
-
Suppose that you have a formula
 of the form
for
of the form
for 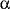 being
being  holds
holds 
or
ex 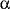 being
being  st
st 
where 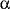 is a object identifier,
is a object identifier,  is a sort.
Then object identifier
is a sort.
Then object identifier 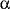 is bound in
is bound in  , the scope of the
quantifier for or ex is all of the free occurrences of
, the scope of the
quantifier for or ex is all of the free occurrences of
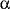 in
in  , and all of (and only) the free occurrences of
, and all of (and only) the free occurrences of 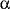 in
in
 are bound in
are bound in  to the quantifier for or ex.
All other free occurrences of any object identifier in
to the quantifier for or ex.
All other free occurrences of any object identifier in  are still free in
are still free in
 .
.
We now do a couple of examples.
The important thing to remember is that determining the bindings of object
identifiers in a logical formula is exactly the same problem as determining
the bindings of variable names in a programming language.
Consider the following formula:
for x,y being THING holds (x=y or P[z] & (ex y being BLOB st B[x,y]))
To determine the binding of each of the object identifiers x,y, and
z in this formula we apply the rules we just introduced.
We begin by looking at the lowest level component
B[x,y]
in which x, y are both free by rule 1.
This formula is quantified to make a new statement
ex y being BLOB st B[x,y]
in which x is still free, but y is now bound to the ex
quantifier by rule 3.
Now z is free in P[z], and so when we apply rule 2 to construct
P[z] & (ex y being BLOB st B[x,y])
we have all occurrences of x and z being free, and all occurrences
of y being bound.
Since x and y are free in x=y, when we apply rule 2 to
construct
x=y or P[z] & (ex y being BLOB st B[x,y])
we get that
all occurrences of x and z are free, the first occurrence of
y is free, and the other occurrences of y are bound.
Finally, applying rule 3 we get
for x,y being THING holds (x=y or P[z] & (ex y being BLOB st B[x,y]))
which has all occurrences of x and the first occurrence of y
bound to the for universal quantifier;
the second occurrence of y being bound to the ex
existential quantifier; and all occurrences of z being free.
Here is another example.
Formulas 1 and 2 have the same bindings, while 3 does not.
(Remember that a quantifier with a list of object identifiers is
simply a short form for a sequence of quantifiers, one for each
object identifier.)
1: for x, y, z being THING holds R[x,y,z]
2: for x being THING holds
for y being THING holds
for z being THING holds R[x,y,z]
3: for x, z, y being THING holds R[x, y, z]
3.7: The Semantics of Quantified Formulas
What meaning do we give to quantified formulas?
Suppose that 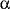 is an object identifier,
is an object identifier,  is a sort identifier,
and
is a sort identifier,
and  is a formula with free occurrences of variable
is a formula with free occurrences of variable 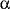 .
Then a universally quantified formula
.
Then a universally quantified formula
for 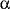 being
being  holds
holds 
is true exactly when  is true no matter what object of sort
is true no matter what object of sort  is
is named by
is
is named by 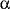 .
If
.
If  fails to hold for even one such object, the universal formula is
false.
fails to hold for even one such object, the universal formula is
false.
An existentially quantified formula
ex 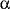 being
being  st
st 
is true exactly when there is at least one object of sort  that satisfies statement
that satisfies statement  .
.
Another way of thinking about the universal and existential quantifiers
is as generalizations of the & and or connectives.
Suppose that the objects of some sort S could be completely enumerated
as the objects a, b, c, d.
Then saying
for x being S holds P[x]
is equivalent to the formula
P[a] & P[b] & P[c] & P[d]
Similarly, saying
ex x being S st Q[x]
is equivalent to the formula
Q[a] or Q[b] or Q[c] or Q[d]
We will do some examples later when we look at translations.
3.8: BNF Grammar for Quantified Formulas
Here is the general syntax for a quantified formula.
The first rules are used to specify the list of object identifiers being quantified
along with their sorts.
This list is a shorthand abbreviation of what is to be considered
as a number of quantifications, each one applying to only a single identifier.
This will be explained when we begin to do inferences using quantified
formulas.
| QualifiedObjects ::= | QualifiedSegment { , QualifiedSegement } |
| QualifiedSegment ::= | ObjectId { , ObjectId } ( be | being ) SortId |
The actual quantified formula is given by
| QuantifiedFormula ::= | UniversalFormula | ExistentialFormula |
| UniversalFormula ::= | for QualifiedObjects holds Formula |
| ExistentialFormula ::= | ex QualifiedObjects st Formula |
 and
and  stand for arbitrary MIZAR sentences,
except that we assume that the sentences are enclosed in ().
This avoids some technical difficulties caused by operators having
unequal precedence.
(Consider the case of placing an & between the formulas
P[] or Q[] and R[] or S[].
If we did not enclose each formula in parentheses, placing an &
between them would result in the formula
P[] or Q[] & R[] or S[] instead of our intended
one of (P[] or Q[]) & (R[] or S[]).
Users of macro processors are familiar with this problem.)
stand for arbitrary MIZAR sentences,
except that we assume that the sentences are enclosed in ().
This avoids some technical difficulties caused by operators having
unequal precedence.
(Consider the case of placing an & between the formulas
P[] or Q[] and R[] or S[].
If we did not enclose each formula in parentheses, placing an &
between them would result in the formula
P[] or Q[] & R[] or S[] instead of our intended
one of (P[] or Q[]) & (R[] or S[]).
Users of macro processors are familiar with this problem.)
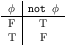
 being
being  holds
holds