Logical formulas by themselves have no meaning or truth-value. To assign meaning to a formula we must specify an interpretation. The interpretation must provide sufficient information for us to determine whether the formula is true or false.
Each interpretation must specify two things:
The degree of detail required by an interpretation varies with the formula that you are trying to interpret. For example the formula
only involves predicates of 0 arity. A complete interpretation would require you to only state whether each atomic formula was true or false. But there are circumstances where having only a partial specification of the truth-values of the predicates would still permit you to interpret the formulas. For example if P[] is true and R[] is true we do not need to know the interpretation of Q[] in order to determine that the formula is true. Another case would be where P[] was false.
A more complicated situation occurs when the predicates have arguments, but the arguments are all constants. For example
To interpret this formula we need to know what the sort of object Fred is, and whether it is of a sort required by the predicates Knight and Knave. We also need to know whether Knight[Fred] and Knave[Fred] are true or false. This could be specified explicitly, for example by saying Knight[Fred] is true, or implicitly, for example by saying that the Knight predicate is always true.
The more common situation is the case where you have a quantified formula such as
for x being PERSON holds
Likes[Fred,x] & ( ex y being PERSON st not Likes[y,Fred] )
One possible interpretation could be that the Likes predicate is always applied to arguments of sort PERSON, and that Likes[a,b] is intended to mean that person a likes person b. In addition, Fred likes everyone, but Wilma does not like Fred. Under this interpretation the formula is true.
Note how the generality of the interpretation increases as the formulas we want to interpret become more complex.
Consider these formulas in which all the predicates are of 0 arity.
Under this interpretation
Formula (1) is false and formula (2) is true.
An interpretation that makes a formula 
true is called a
satisfying interpretation for .
An interpretation that makes a formula false is called a
falsifying interpretation.
Some formulas are true no matter what interpretation you use.
This is the case for formula (2) above.
Such a formula is called a tautology.
The sentence P[] or not P[] is an example
of one of the more important tautologies.
Similarly, some formulas are false under any interpretation. Such a formula is called a contradiction. The formula Knight[x] & not Knight[x] is an example one of the more important contradictions.
Formulas that have both satisfying and falsifying interpretations are called contingencies. The simplest contingency is a formula like P[].
MIZAR has the built-in ability to reason about formulas in which all predicates are either 0-ary or applied to constants. Thus one way to determine if something is a tautology using MIZAR is merely to state it. If MIZAR accepts it, then it is a tautology. (If not, it may still be a tautology but MIZAR ran out of resources while trying to prove it.) For example, MIZAR will accept the following facts without any justification.
environ
begin == DeMorgan's Laws
not ( Phi[] & Psi[] ) iff ( not Phi[] or not Psi[] );
not ( Phi[] or Psi[] ) iff ( not Phi[] & not Psi[] );
( Phi[] & Psi[] ) iff not ( not Phi[] or not Psi[] );
( Phi[] or Psi[] ) iff not ( not Phi[] & not Psi[] );
This verifies four very useful equivalences, called DeMorgan's Laws, which permit you to change a formula using & into a formula using or and vice-versa.
How do you use MIZAR to determine if a formula is a contradiction?
If formula is always false, then not is always true.
Thus, to show that something is a contradiction we simply verify that
its negation is a tautology.
For example:
environ
begin
== Verify that Phi[] & not Phi[] is a contradiction.
not ( Phi[] & not Phi[]);
== Verify that Phi[] iff not Phi[] is a contradiction.
not ( Phi[] iff not Phi[] );
When a formula is neither a tautology nor a contradiction, how do you go about finding a satisfying or falsifying interpretation? One way, which works well for formulas that are short and contain only 0-ary predicates or predicates applied to constants is to compute the truth-value of the formula under all possible truth assignments to the predicates of the formula. For example, the truth-table for not P[] or (P[] implies Q[]) is:
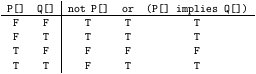
Each line of the table corresponds to one possible interpretation. Thus the formula has three satisfying interpretations and one falsifying.
Since each atomic sentence can be either true or false, the number of possible interpretations for a formula containing n distinct atomic sentences is 2n. Thus the truth-table method does not work so well when the number of predicates gets much larger than five or so. The size of the table quickly becomes unmanageable, at least for humans.
environ == Examples of Translations to Predicate Calculus Formulas
== We will use the basic sorts
== PERSON -- an inhabitant of the island.
== STATEMENT -- a sentence in the language of the island.
== LOCATION -- a place on the island.
== Some basic constants:
given Fred being PERSON;
given Promise being STATEMENT;
given Bedrock, Edmonton being LOCATION;
== The following predicates will be used for any x of sort PERSON, s of
== sort STATEMENT, and p of sort LOCATION with the intended meaning:
== Knight[x] means that x is a knight.
== Knave[x] x is a knave.
== Normal[x] x is a normal.
== Tells[x,s] x says the statement s.
== True[s] statement s is true.
== LivesIn[x,p] x lives in location p.
== Now we do some example translations:
== Every person is a knight, knave, or normal. This is not exclusive,
== a person could be one or more.
1: for y being PERSON holds Knight[y] or Knave[y] or Normal[y];
== There is a person called Sam who lives in Edmonton, and the
== only false thing that Sam says is the statement Promise.
given Sam being PERSON;
2: LivesIn[Sam,Edmonton] &
(for s being STATEMENT
holds Tells[Sam,s] & not True[s] implies s=Promise);
== If any knight makes a statement then that statement is true.
== Alternatively, knights always tell the truth.
3: for y being PERSON, s being STATEMENT holds
Knight[y] & Tells[y,s] implies True[s];
== Every normal person tells at least one truth and at least one lie.
4: for x being PERSON holds Normal[x] implies
(ex s,t being STATEMENT st
Tells[x,s] & Tells[x,t] & True[s] & not True[t]);
== There is at least one statement that is both said by some
== resident of Edmonton and not said by some resident of Edmonton.
5: ex s being STATEMENT st
ex y,z being PERSON st LivesIn[y, Edmonton] & LivesIn[z, Edmonton] &
Tells[y,s] & not Tells[z,s];
== Every inhabitant of Bedrock tells the truth.
== Statements 6 and 7 are two ways of saying this.
6: for x being PERSON, s being STATEMENT holds
LivesIn[x, Bedrock] & Tells[x,s] implies True[s];
7: for x being PERSON holds LivesIn[x,Bedrock] implies
(for s being STATEMENT holds Tells[x,s] implies True[s]);
== No inhabitant of Bedrock lies. This is logically equivalent to both
== of the preceding statements.
7': not ( ex x being PERSON, s being STATEMENT st
LivesIn[x,Bedrock] & Tells[x,s] & not True[s] );
== Some inhabitants of Edmonton are normal, and some are knights.
8: (ex x being PERSON st LivesIn[x,Edmonton] & Normal[x]) &
(ex x being PERSON st LivesIn[x,Edmonton] & Knight[x]);
== If a normal person always tells the truth then they are also a knight.
9: for x being PERSON holds
Normal[x] &
(for s being STATEMENT holds Tells[x,s] implies True[s])
implies Knight[x];
== Fred tells exactly one lie.
10: ex Lie being STATEMENT st (
Tells[Fred, Lie] & not True[Lie] &
( for Lie2 being STATEMENT holds
(Tells[Fred,Lie2] & not True[Lie2] implies Lie = Lie2)) );
== Some normal persons tell the truth all of the time, and some of the time
== all of the normals tell the truth, but it is not the case that
== all of the normals tell the truth all of the time.
== How to translate the phrases "all of the time" and "some of the time".
== I took this as meaning "every statement they make" and
== "some statement they make". This removes "time" from the translation.
== Another problem is figuring out what "some of the time all of the
== normals tells the truth" means. I took this as meaning that
== at least one sentence was stated truthfully by all normals.
11: ( ex x being PERSON st (Normal[x] &
(for s being STATEMENT holds Tells[x,s] implies True[x]) ))
& ( ex s being STATEMENT st (True[s] &
(for x being PERSON holds Normal[x] implies Tells[x,s]) ))
& not ( for x being PERSON, s being STATEMENT holds
Normal[x] & Tells[x,s] implies True[s] );
environ
given 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 being NATURAL;
== The universe of discourse is the set of natural numbers (NATURAL).
== Translate each of the following statements into syntactically correct
== formulas, using the following scheme of abbreviation.
== Even[x] x is an even number
== Odd[x] x is an odd number
== Prime[x] x is a prime number
== Divisible[x,y] x is (evenly) divisible by y
== Examples:
== 1: 2 is an even prime.
1: Even[2] & Prime[2];
== 2: 6 is not a prime because 3 divides it.
2: Divisible[6,3] implies not Prime[6];
== End of examples
== 1: Neither 4 nor 6 is a prime number.
== 2: Neither 8 nor 7 is a prime number.
== 3: If 6 divides 9 then 9 is not a prime.
== 4: 10 is a product of 2 and 5.
== Watch out, the answer is not
== 4: Divisible[10,2] & Divisible[10,5];
== 5: 5 is a prime because it is divisible only by 1 and itself.
== 6: No even number is odd.
== 7: Not all odd numbers are prime.
== 8: There is exactly one even prime.
== 9: No prime is neither even or odd.
== 10: 2 is the only even prime number.
== 11: Every non-prime is divisible by at least one prime.
== 12: There are non-primes that are not divisible by any odd prime.
== 13: Every prime number is not divisible by any number but 1 and itself.
== Final remark. Run your stuff through Mizar. So long as your translations
== appear in the environment section, and they are syntactically correct,
== they will be accepted by Mizar.
environ
given 1,2,3,4,5,6,7,8,9,10 being NATURAL;
1: not (Prime[4] or Prime[6]);
2: not (Prime[8] or Prime[7]);
3: Divisible[9,6] implies not Prime[9];
4: Divisible[10,2] & Divisible[10,5] &
(for X being NATURAL
holds Divisible[10,X] implies X=1 or X=2 or X=5 or X=10);
5: Divisible[5,1] & Divisible[5,5] &
(for X being NATURAL holds Divisible[5,X] implies X=1 or X=5)
implies Prime[5];
6: for X being NATURAL holds Even[X] implies not Odd[X];
7: not (for X being NATURAL holds Odd[X] implies Prime[X]);
8: ex X being NATURAL st Even[X] & Prime[X] &
(for Y being NATURAL holds Even[Y] & Prime[Y] implies Y=X);
9: for X being NATURAL holds Prime[X] implies Even[X] or Odd[X];
10: for X being NATURAL holds Even[X] & Prime[X] implies X=2;
11: for X being NATURAL holds not Prime[X]
implies (ex Y being NATURAL st Prime[Y] & Divisible[X,Y]);
12: ex X being NATURAL st not Prime[X] &
(for Y being NATURAL
holds Odd[Y] & Prime[Y] implies not Divisible[X,Y]);
13: for X being NATURAL holds Prime[X] implies
(for Y being NATURAL
holds Y<>X & Y<>1 implies not Divisible[X,Y]);