Spatial Inversion

We now consider the improper Lorentz transformation of reflection in space or the parity transformation:

$$\vec{x}^\prime=-\vec{x}\quad \textrm{and}\quad t^\prime = t.$$ (5.149)

We need to solve (5.122) for

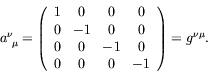$$a^\nu_{\ \mu} = \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ ... ...& -1 & 0 \\ 0 & 0 & 0 & -1 \end{array}\right) = g^{\nu\mu} .$$ (5.150)

We denote the Lorentz operator $S(a)$ by $P$ for parity. Consider the following ansatz

$$P=e^{i\phi}\gamma_0,$$ (5.151)

where $\phi$ is an arbitrary phase. Using equation 5.122, we have

$$e^{-i\phi}\gamma_0\gamma^\nu e^{i\phi}\gamma_0 = \gamma^0\gamma^\nu\gamma^0 = g^{\nu\mu} \gamma^\mu ,$$ (5.152)

as required.

In analogy to the proper Lorentz transformation for which a rotation of $4\pi$ reproduces the original spinors, we postulate that four space-inversions will reproduce the original spinors.

$$P^4\psi = \psi = (e^{i\phi}\gamma^0)^4\psi = e^{i4\phi} (\gamma^0)^4\psi = e^{i4\phi} \psi .$$ (5.153)

Therefore

$$e^{i4\phi} = 1 \Rightarrow e^{i\phi} = \pm 1 \ \textrm{or}\ \pm i .$$ (5.154)

We see that

$$P^{-1} = e^{-i\phi} \gamma^{-1}_0 = e^{-i\phi} \gamma_0,$$ (5.155)

$$P^\dagger = e^{-i\phi} \gamma^\dagger_0 = e^{-i\phi} \gamma_0$$ (5.156)

and $P^{-1} = P^\dagger \Rightarrow P$ is unitary.

The wave function thus transforms as

$$\psi^\prime(x^\prime) = \psi^\prime(-\vec{x},t) = e^{i\phi}\gamma_0\psi(\vec{x},t) .$$ (5.157)

In the nonrelativisitc limit $\psi$ approaches an eigenstate of $P$. The positive- and negative-energy states at rest have opposite eigenvalues, or intrinsic parities. The intrinsic parity of a Dirac particle and antiparticle are opposite. This is to be contrasted to the Klein-Gordon case wherein one finds identical parities for the particle and antiparticle solutions.