Lorentz Boosts

For an arbitrary direction of $\hat{v}=\vec{v}/\vert\vec{v}\vert$, we may write in terms of the direction cosines:

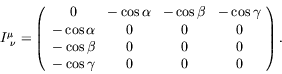$$I^\mu_{\ \nu} = \left( \begin{array}{cccc} 0 & -\cos\alpha &... ...& 0 & 0 & 0 \\ -\cos\gamma & 0 & 0 & 0 \end{array} \right) .$$ (5.144)

Raising the $\nu$ index makes $I^{\mu\nu}$ anti-symmetric. Also $\sigma_{\mu\nu}$ is anti-symmetric. Therefore

$$\sigma_{\mu\nu}I^{\mu\nu} = 2(\sigma_{01}\cos\alpha + \sigma_{02}\cos\beta + \sigma_{03}\cos\gamma)$$

$$= 2i(\gamma_0\gamma_1\cos\alpha + \gamma_0\gamma_2\cos\beta + \gamma_0\gamma_3\cos\gamma)$$

$$= -2i(\alpha_1\cos\alpha + \alpha_2\cos\beta + \alpha_3\cos\gamma)$$

$$= -2i\vec{\alpha}\cdot\hat{v} .$$ (5.145)

From the properties of the $\alpha_i$ matrices, we have

$$(\vec{\alpha}\cdot\hat{v})^2 = 1 .$$ (5.146)

The finite spinor transformation for a general Lorentz boost becomes

$$S = \exp\left(-\frac{\omega}{2} \vec{\alpha}\cdot\hat{v} \right)$$

$$= \cosh\left(-\frac{\omega}{2}\vec{\alpha}\cdot\hat{v}\right) + \sinh\left(-\frac{\omega}{2}\vec{\alpha}\cdot\hat{v}\right)$$

$$= \cosh\left(\frac{\omega}{2}\vec{\alpha}\cdot\hat{v}\right) - \sinh\left(\frac{\omega}{2}\vec{\alpha}\cdot\hat{v}\right)$$

$$= \cosh\frac{\omega}{2} -\vec{\alpha}\cdot\hat{v} \sinh\frac{\omega}{2}$$

$$= \cosh\frac{\omega}{2} \left(1 - \vec{\alpha}\cdot\hat{v} \tanh\frac{\omega}{2}\right).$$ (5.147)

For a Lorentz boost $S^\dagger\neq S^{-1}$. However, by expanding $S$ in a power series, it has the property

$$\fbox{$\displaystyle S^{-1} = \gamma_0 S^\dagger \gamma_0 $}\ .$$ (5.148)

This can also be generalized to include rotations.