Consider a rotation through an angle ![]() about the
about the ![]() -axis:
-axis:
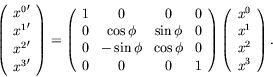 |
(5.140) |
The matrix ![]() has all zero elements accept for
has all zero elements accept for
![]() , or
, or
![]() .
Thus
.
Thus
| (5.141) |
Therefore
| (5.142) |
For a rotation about an arbitrary axis ![]() , we write
, we write
| (5.143) |
The appearance of the half-angle is an expression of the
double-valuedness of the spinor law of rotation; it takes a rotation of
![]() to return
to return ![]() to its original value.
This is a characteristic of 1/2 integer spin.
Therefore physical observables in the Dirac theory must be bilinear,
or an even power in
to its original value.
This is a characteristic of 1/2 integer spin.
Therefore physical observables in the Dirac theory must be bilinear,
or an even power in ![]() .
By using the rotation operator upon the solution for the Dirac
particle at rest and polarized in the
.
By using the rotation operator upon the solution for the Dirac
particle at rest and polarized in the ![]() -direction, it is possible
to form states of any arbitrary direction.
Since
-direction, it is possible
to form states of any arbitrary direction.
Since ![]() is hermitian,
is hermitian,
![]() for spatial
rotations.
We shall henceforth call the wave function of the Dirac theory a
spinor.
for spatial
rotations.
We shall henceforth call the wave function of the Dirac theory a
spinor.