Free Motion of a Dirac Particle

Consider the Dirac equation without potentials (free equation)

$$i\hbar\frac{\partial\psi}{\partial t} = \hat{H}_f\psi = (c\vec{\alpha}\cdot \hat{p} + mc^2\beta)\psi .$$ (5.59)

Its stationary states are found with the ansatz

$$\psi_\lambda(\vec{x},t) = \psi(\vec{x}) e^{-i\lambda Et/\hbar} ,$$ (5.60)

where $\lambda=\pm 1$, and

$$\hat{H}_f\psi = i\hbar\psi(\vec{x}) (-i\lambda E/\hbar) e^{-i\lambda Et/\hbar} ,$$

$$= \lambda E\psi .$$ (5.61)

We split up the 4-component spinor into two 2-component spinors $\phi$ and $\chi$ to give

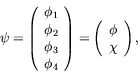$$\psi = \left( \begin{array}{c}\phi_1\\ \phi_2\\ \phi_3\\ \p... ...ght) = \left( \begin{array}{c}\phi\\ \chi\end{array}\right) ,$$ (5.62)

where

$$\phi=\left(\begin{array}{c}\phi_1 \\ \phi_2\end{array}\right... ...\chi=\left(\begin{array}{c}\phi_3 \\ \phi_4\end{array}\right).$$ (5.63)

Substituting our definitions into the Dirac equation we have

$$\lambda E \left( \begin{array}{c}\phi\\ \chi\end{array} \rig... ...ight) \left ( \begin{array}{c}\phi\\ \chi\end{array} \right) ,$$ (5.64)

$$\lambda E\phi = c\vec{\sigma}\cdot\hat{p}\chi + mc^2\phi,$$ (5.65)

$$\lambda E\chi = c\vec{\sigma}\cdot\hat{p}\phi - mc^2\chi.$$ (5.66)

States with definite momentum can be written as

$$\left( \begin{array}{c}\phi\\ \chi\end{array} \right) = \lef... ...\\ \chi_0\end{array} \right) e^{i\vec{p}\cdot\vec{x}/\hbar} .$$ (5.67)

We recognize that these states are eigenfunctions of the momentum operator:

$$\hat{p}\psi_{\vec{p}\lambda}(\vec{x},t) = \vec{p}\psi_{\vec{p}\lambda}(\vec{x},t) .$$ (5.68)

Substitution into equations 5.65 and 5.66 gives

$$\lambda E\phi_0 = c\vec{\sigma}\cdot\vec{p}\chi_0 + mc^2\phi_0 ,$$ (5.69)

$$\lambda E\chi_0 = c\vec{\sigma}\cdot\vec{p}\phi_0 - mc^2\chi_0 .$$ (5.70)

Rearranging we have

$$(\lambda E-mc^2)\phi_0 - c\vec{\sigma}\cdot\vec{p}\chi_0 = 0 ,$$ (5.71)

$$- c\vec{\sigma}\cdot\vec{p}\phi_0 + (\lambda E+mc^2)\chi_0 = 0 .$$ (5.72)

For a solution we require

$$\lambda^2 E^2 - m^2c^4 - c^2(\vec{\sigma}\cdot\vec{p})^2 = 0.$$ (5.73)

Using identity 2.24 we have

$$E = \lambda\sqrt{\vec{p}^{\ 2}c^2 + m^2c^4} ,$$ (5.74)

where we have been careful with the sign of $\lambda$ when solving for both cases at ones.

We also have

$$\chi_0 = \frac{c\vec{\sigma}\cdot\vec{p}}{mc^2+\lambda E} \p... ...0 = \frac{c\vec{\sigma}\cdot\vec{p}}{-mc^2+\lambda E} \chi_0 .$$ (5.75)

Let us denote the two-component spinor $\phi_0$ by

$$\phi_0 = u = \left( \begin{array}{c}u_1\\ u_2\end{array} \right),$$ (5.76)

where $u_1$ and $u_2$ are complex and $u$ is normalized according to $u^\dagger u = u_1^*u_1 + u_2^*u_2=1$.

The complete set of positive- and negative-energy free solutions is

$$\psi_{\vec{p}\lambda}(\vec{x},t) = N \left( \begin{array}{c}... ...rray}\right) e^{[i(\vec{p}\cdot\vec{x} - \lambda Et)/\hbar]} .$$ (5.77)

The normalization $N$ is determined from

$$\int d^3x {\psi_{\vec{p}\lambda}}^\dagger(\vec{x},t) \psi_{\... ...delta_{\lambda\lambda^\prime} \delta(\vec{p}-\vec{p}^\prime) .$$ (5.78)

$$N^2 \left( u^\dagger u + u^\dagger \frac{c^2(\vec{\sigma}\cdot\vec{p})(\vec{\sigma}\cdot\vec{p})} {(mc^2+\lambda E)^2} u\right) = 1 ,$$

$$N^2 \left( 1 + \frac{c^2\vec{p}^2}{(mc^2+\lambda E)^2} \right) = 1 ,$$ (5.79)

or

$$N = \sqrt{\frac{(mc^2+\lambda E)^2}{(mc^2+\lambda E)^2 + c^2\vec{p}^{\ 2}}} ,$$

$$N = \sqrt{\frac{(mc^2+\lambda E)^2}{m^2c^4+E^2+2\lambda mc^2E+c^2\vec{p}^2}} ,$$

$$N = \sqrt{\frac{(mc^2+\lambda E)^2}{2E(E+\lambda mc^2)}} ,$$

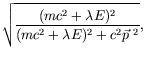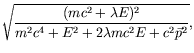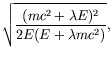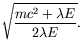$$N = \sqrt{\frac{mc^2+\lambda E}{2\lambda E}} .$$ (5.80)

We now show that another quantum number, helicity, can be used to classify free one-particle states. Define

$$\hat{s} = \frac{\hbar}{2} \vec{\Sigma} = \frac{\hbar}{2} \le... ...rray}{cc}\vec{\sigma}&0\\ 0&\vec{\sigma}\end{array} \right) .$$ (5.81)

This is the four dimensional generalization of the spin vector operator.

We form

$$\vec{\Sigma}\cdot\hat{p} = \left( \begin{array}{cc}\vec{\sigma}&0\\ 0&\vec{\sigma}\end{array}\right)\cdot\hat{p}$$ (5.82)

and show that it commutes with the free Dirac Hamiltonian operator.

$$[\hat{H}_f,\vec{\Sigma}\cdot\hat{p}]= [c\hat{\alpha}\cdot\hat{p} + mc^2\hat{\beta},\vec{\Sigma}\cdot\hat{p}] .$$ (5.83)

Since $[\hat{\beta},\vec{\Sigma}]=0$, we need only consider

$$[\hat{H}_f,\vec{\Sigma}\cdot\hat{p}] = c[\hat{\alpha}\cdot\hat{p}, \vec{\Sigma}\cdot\hat{p}]$$

$$= c\hat{\alpha}\cdot\hat{p}\vec{\Sigma}\cdot\hat{p} - c \vec{\Sigma}\cdot\hat{p}\hat{\alpha}\cdot\hat{p}$$

$$= c\left( \begin{array}{cc} 0&\vec{\sigma}\cdot\hat{p}\\ \vec{\sig... ...c} 0&\vec{\sigma}\cdot\hat{p}\\ \vec{\sigma}\cdot\hat{p}&0 \end{array} \right)$$

$$= c\left( \begin{array}{cc} 0&(\vec{\sigma}\cdot\hat{p})^2\\ (\vec... ...vec{\sigma}\cdot\hat{p})^2\\ (\vec{\sigma}\cdot\hat{p})^2&0 \end{array}\right)$$

$$= 0 .$$ (5.84)

Also $[\hat{p},\vec{\Sigma}\cdot\hat{p}]=0$, therefore $\vec{\Sigma}\cdot\hat{p}, \hat{H}_f, \hat{p}$ can all be diagonalized together.

$\vec{\Sigma}\cdot\hat{p}$ can be rewritten as the helicity operator

$$\hat{\Lambda}_S = \frac{\hbar}{2} \vec{\Sigma}\cdot\frac{\ha... ...ec{p}\vert} = \hat{s}\cdot\frac{\hat{p}}{\vert\vec{p}\vert} .$$ (5.85)

Helicity is the projection of the spin onto the direction of the momentum.

For an electron propagating in the $z$-direction $\vec{p}=(0,0,p)$,

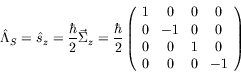$$\hat{\Lambda}_S = \hat{s}_z = \frac{\hbar}{2} \vec{\Sigma}_z... ...} 1&0&0&0\\ 0&-1&0&0\\ 0&0&1&0\\ 0&0&0&-1 \end{array} \right)$$ (5.86)

with eigenvalues $\pm\hbar/2$. The eigenvectors of $\hat{\Lambda}_S$ are

$$\left(\begin{array}{c} u_1\\ 0 \end{array}\right), \quad \le... ...), \quad \left(\begin{array}{c} 0\\ u_{-1} \end{array}\right),$$ (5.87)

with

$$u_1 = \left(\begin{array}{c} 1\\ 0 \end{array}\right) \quad ... ...quad u_{-1} = \left(\begin{array}{c} 0\\ 1 \end{array}\right).$$ (5.88)

We can write $\psi_{p_z,\lambda,s_z}(\vec{x},t)$, where

$$\psi_{p_z,\lambda,+1/2} = N \left(\begin{array}{c} \left(\begin{array}{c} 1 \\ 0 \end{arra... ...}{c} 1 \\ 0 \end{array}\right) \end{array}\right) e^{[i(pz-\lambda Et)/\hbar]}$$ (5.89)

$$\psi_{p_z,\lambda,-1/2} = N \left(\begin{array}{c} \left(\begin{array}{c} 0 \\ 1 \end{arra... ...}{c} 0 \\ 1 \end{array}\right) \end{array}\right) e^{[i(pz-\lambda Et)/\hbar]}$$ (5.90)

and

$$\int d^3x {\psi_{p_z,\lambda,s_z}}^\dagger\psi_{p_z^\prime,\... ...ambda^\prime} \delta_{s_zs_z^\prime} \delta(p_z-p_z^\prime) .$$ (5.91)

We thus see that we have two independent states for a positive-energy electron:

$$\phi^1 = \left(\begin{array}{c} 1 \\ 0 \end{array}\right) \quad\textrm{spin up} ,$$ (5.92)

$$\phi^2 = \left(\begin{array}{c} 0 \\ 1 \end{array}\right) \quad\textrm{spin down} .$$ (5.93)

We expect the absence of ``spin-up'' to be equivalent to the presence of ``spin-down''. This implies that a negative-energy solution with spin down is equivalent to a positive-energy solution with spin up. We choose

$$\chi^1 = \left(\begin{array}{c} 1 \\ 0 \end{array}\right) ,$$ (5.94)

$$\chi^2 = \left(\begin{array}{c} 0 \\ 1 \end{array}\right) .$$ (5.95)

Why dose the Dirac spinor need four components to describe a spin-1/2 particle? The answer has to do with parity. in a relativistic theory, we would not be able to represent the effect of parity satisfactorily with only two components.