Wave Equation for a Spin-1/2 Particle

We seek a relativistic covariant equation of the form

$$i\hbar\frac{\partial\psi}{\partial t} = \hat{H}\psi ,$$ (5.1)

which is first order in the time derivative and will have positive definite probability density. Assuming such an equation is also linear in the space derivatives, we can write

$$i\hbar\frac{\partial\psi}{\partial t} = \frac{\hbar c}{i} \l... ...3\frac{\partial\psi}{\partial x^3} \right) + \beta mc^2\psi .$$ (5.2)

Using operator notation we have

$$\fbox{$\displaystyle i\hbar\frac{\partial\psi}{\partial t} =... ...( c \vec{\alpha} \cdot \hat{p} + \beta mc^2 \right) \psi $}\ .$$ (5.3)

For invariance under spatial rotation, the $\alpha_i$ can not be numbers and $\psi$ can not be a scalar. In analogy with the spin wave function of nonrelativistic quantum mechanics, we choose $\psi$ to be a vector, and $\alpha_i$ and $\beta$ to be matrices. Explicitly,

$$i\hbar\frac{\partial\psi_\sigma}{\partial t} = \sum_{\tau=1}... ...\psi_\tau + \sum_{\tau=1}^N \beta_{\sigma\tau} mc^2\psi_\tau .$$ (5.4)

We thus have $N$ coupled first-order equations.

These equations must

1. have free-particle solutions that satisfy $E^2=\vec{p}^{\ 2}c^2 + m^2c^4$,
2. yield a continuity equation and probability interpretation of $\psi$, and
3. be Lorentz covariant.

For the first condition to be satisfied, each component of $\psi_\sigma$ must satisfy the Klein-Gordon equation. Applying the operator (5.1) twice gives

$$\left(i\hbar\frac{\partial}{\partial t}\right)\left(i\hbar\frac{\partial}{\partial t}\right)\psi = (\hat{H})(\hat{H})\psi$$

$$-\hbar^2 \frac{\partial^2\psi}{\partial t^2} = -\hbar^2 c^2 \left( \sum_{i=1}^3 \alpha_i \frac{\partial}{\partia... ... \right)\left( \sum_{j=1}^3 \alpha_j \frac{\partial}{\partial x^j} \right) \psi$$

$$+ \frac{\hbar mc^3}{i} \sum_{i=1}^3 (\alpha_i\beta + \beta\alpha_i) \frac{\partial\psi}{\partial x^i} + \beta^2 m^2 c^4 \psi$$

$$= -\hbar^2 c^2 \sum_{i,j=1}^3 \frac{\alpha_i\alpha_j + \alpha_j\alpha_i}{2} \frac{\partial^2\psi}{\partial x^i\partial x^j}$$

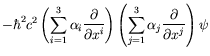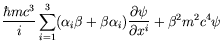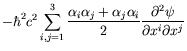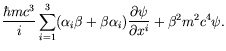$$+ \frac{\hbar mc^3}{i} \sum_{i=1}^3 (\alpha_i\beta + \beta\alpha_i) \frac{\partial\psi}{\partial x^i} + \beta^2 m^2c^4\psi .$$ (5.5)

To obtain the Klein-Gordon equation the following must be satisfied

$$\alpha_i\alpha_j + \alpha_j\alpha_i = 2\delta_{ij} ,$$ (5.6)

$$\alpha_i\beta + \beta\alpha_i = 0,$$ (5.7)

$$\alpha^2_i = \beta^2 = I ,$$ (5.8)

where $I$ represents an $N\times N$ unit matrix. We will not write the unit matrix explicitely in the wave equation unless it is required for clarity. This should not create any confusion since matrices can only equal matrices.

No terms in the Hamiltonian can have any space or time coordinates. Such terms would have the property of space-time dependent energies and would give rise to forces. Space and time derivatives can only appear in $\hat{p}$ and $\hat{E}$, but not in $\alpha_i$ and $\beta$, since the equation is to be linear in these derivatives. Thus $\alpha_i$ and $\beta$ are independent of $\vec{r}, t, \vec{p}, E$ and hence commute with them.

Since the Hamiltonian must be hermitian, $\alpha_i$ and $\beta$ must be hermitian matrices. Since the matrices are hermitian they must be square.

Since $\alpha_i$ and $\beta$ anticommute according to equation 5.7, they are traceless. This can be seen as follows:

$$\beta\alpha_i = -\alpha_i\beta$$

$$\alpha_i = -\beta\alpha_i\beta$$

$$\textrm{Tr}(\alpha_i) = -\textrm{Tr}(\beta\alpha_i\beta) = -\textrm{Tr}(\beta^2\alpha_i) = -\textrm{Tr}(\alpha_i) = 0 .$$ (5.9)

where the last line follows from the cyclic property of the trace. The choice of $\vec{\alpha}$ and $\beta$ is not unique. All matrices related to these by any unitary $N\times N$ matrix $U$ (which preserves the anti-commutation relations) are allowed: $\alpha_i^\prime = U\alpha_i U^{-1}$ and $\beta^\prime = U\beta U^{-1}$.

Since $\alpha_i^2=\beta^2=1$, the eigenvalues of $\alpha_i$ and $\beta$ are $\pm 1$. Since the trace is the sum of eigenvalues $\alpha_i$ and $\beta$, must be of even dimensions. For $N=2$, only three anti-commuting matrices exist (the Pauli matrices). Thus the smallest dimension allowed is $N=4$.

If one matrix is diagonal, the others can not be diagonal or they would commute with the diagonal matrix. We can write a representation that is hermitian, traceless, and has eigenvalues of $\pm 1$:

$$\alpha_i = \left( \begin{array}{cc} 0 & \sigma_i \\ \sigma... ...eft( \begin{array}{cr} I & 0 \\ 0 & -I \end{array}\right) ,$$ (5.10)

where $\sigma_i$ are the $2\times 2$ Pauli matrices and $I$ is the $2\times 2$ unit matrix.