Zitterbewegung

Consider a wavepacket containing only positive-energy components

$$\phi(\vec{x},t) = \int \frac{d^3p}{(2\pi)^3} e^{i\vec{p}\cdot\vec{x}} a^{(+)}_{\vec{p}}(t) \chi^{(+)}(\vec{p}) ,$$ (4.123)

where

$$a^{(+)}_{\vec{p}}(t) = e^{-iE_pt} f([\vec{p}-\vec{p}_0]^2)$$ (4.124)

is some function which peaks at the origin in momentum space. For example, a narrow gaussian distribution. A wavepacket beginning at the origin at $t=0$ will move with uniform velocity $\vec{v}_0=\vec{p}_0/E_{p_0}$. If we pick a functional form for $f$ we will find that there is a minimum width of the wavepacket and that it cannot be made smaller so long as only positive-energy components are present. We can also attempt to construct a wavepacket localized at the origin. If one wishes to localize a wavepacket within a distance smaller than a Compton wavelength, negative-energy components are required.

Consider the position operator $\hat{x}$ applied to a positive-energy only wavepacket

$$\hat{x} \phi(\vec{x},t) = \hat{x}\int \frac{d^3p}{(2\pi)^3} ... ...vec{p}\cdot\vec{x}} a^{(+)}_{\vec{p}}(t) \chi^{(+)}(\vec{p}) .$$ (4.125)

Noticing that $\hat{x} \equiv i\vec{\nabla}_{\vec{p}}$, we can write

$$\hat{x} \phi(\vec{x},t) = i \int \frac{d^3p}{(2\pi)^3} \vec{\nabla}_{\vec{p}}[e^{i\vec{p}\cdot\vec{x}} a^{(+)}_{\vec{p}}(t) \chi^{(+)}(\vec{p})] ,$$

$$= - \int \frac{d^3p}{(2\pi)^3} e^{i\vec{p}\cdot\vec{x}} \left[ \vec... ...}(t) - ia^{(+)}_{\vec{p}}(t) \vec{\nabla}_{\vec{p}} \chi^{(+)}(\vec{p}) \right]$$

$$= - \int \frac{d^3p}{(2\pi)^3} e^{\vec{p}\cdot\vec{x}} \left[ \vec{... ...^{(+)} - i\chi^{(+)}(\vec{p})\vec{\nabla}_{\vec{p}}a^{(+)}_{\vec{p}}(t) \right.$$

$$+ \left. i\frac{\vec{p}}{2E_p^2} a^{(+)}_{\vec{p}}(t) \chi^{(-)}(\vec{p}) \right] ,$$ (4.126)

where we have made use of the following identities

$$\vec{\nabla}_{\vec{p}}E = \vec{\nabla}_{\vec{p}}(m^2 + \vec{... .../2(m^2 + \vec{p}^{\: 2})^{-1/2}2\vec{p} = \frac{\vec{p}}{E} ,$$ (4.127)

$$\vec{\nabla}_{\vec{p}} \chi^{(+)}(\vec{p}) = \vec{\nabla}_{\vec{p}} \frac{1}{2\sqrt{mE}} \left( \begin{array}{c} m+E \\ m-E \end{array} \right)$$

$$= -\frac{1}{2} \frac{E^{-3/2}}{2\sqrt{m}} \frac{\vec{p}}{E} \left( ... ...sqrt{m}} \frac{\vec{p}}{E} \left( \begin{array}{r} 1 \\ -1 \end{array} \right)$$

$$= \frac{\vec{p}}{4\sqrt{mE}E^2} \left( \begin{array}{r} 2E-m-E \\ ... ...ec{p}}{4\sqrt{mE}E^2} \left( \begin{array}{c} -m+E \\ -m-E \end{array} \right)$$

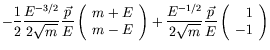$$= -\frac{\vec{p}}{2E^2} \chi^{(-)}(\vec{p}) .$$ (4.128)

Also

$$\vec{\nabla}_{\vec{p}} \chi^{(-)}(\vec{p}) = \vec{\nabla}_{\vec{p}} \frac{1}{2\sqrt{mE}} \left( \begin{array}{c} m-E \\ m+E \end{array} \right)$$

$$= -\frac{1}{2} \frac{E^{-3/2}}{2\sqrt{m}} \frac{\vec{p}}{E} \left( ... ...sqrt{m}} \frac{\vec{p}}{E} \left( \begin{array}{r} -1 \\ 1 \end{array} \right)$$

$$= \frac{\vec{p}}{4\sqrt{mE}E^2} \left( \begin{array}{r} -2E-m+E \\ ... ...ec{p}}{4\sqrt{mE}E^2} \left( \begin{array}{c} -m-E \\ -m+E \end{array} \right)$$

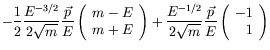$$= -\frac{\vec{p}}{2E^2} \chi^{(+)}(\vec{p}) ,$$ (4.129)

We see in equation 4.126 that the position operator has introduced a negative energy piece into the wave function even though there was none present originally. Equivalently, multiplication by the potential energy $eA^0(\vec{x})$ introduces such negative energy states, so that whenever a wavepacket interacts with a potential we should not be surprised to find negative energy states appearing.

Let us also evaluate the expectation value of the position operator for a wavepacket that is a mixture of positive- and negative-energy components.

$$\langle\phi(t)\vert\hat{x}\vert\phi(t)\rangle = \int d^3x \phi^\dagger(\vec{x},t) \tau_3 \hat{x} \phi(\vec{x},t)$$ (4.130)

$$= \int d^3x \int \frac{d^3p^\prime}{(2\pi)^3} \int \frac{d^3p}{(2\p... ...) {\chi^{(-)}}^\dagger(\vec{p}^\prime) e^{+i\vec{p}^\prime\cdot\vec{x}} \right]$$

$$\tau_3 \hat{x} \left[ a^{(+)}_{\vec{p}}(t) \chi^{(+)}(\vec{p}) e^... ... + a^{(-)}_{\vec{p}}(t) \chi^{(-)}(\vec{p}) e^{-i\vec{p}\cdot\vec{x}} \right] ,$$

$$= i \int d^3x \int \frac{d^3p^\prime}{(2\pi)^3} \int \frac{d^3p}{(2... ...) {\chi^{(-)}}^\dagger(\vec{p}^\prime) e^{+i\vec{p}^\prime\cdot\vec{x}} \right]$$

$$\tau_3 \left[ e^{+i\vec{p}\cdot\vec{x}} \left( \chi^{(+)}(\vec{p}... ...a^{(+)}_{\vec{p}}(t) \vec{\nabla}_{\vec{p}} \chi^{(+)}(\vec{p}) \right) \right.$$

$$+ e^{-i\vec{p}\cdot\vec{x}} \left. \left( \chi^{(-)}(\vec{p}) \ve... ...{(-)}_{\vec{p}}(t) \vec{\nabla}_{\vec{p}} \chi^{(-)}(\vec{p}) \right) \right] ,$$ (4.131)

where we have droped the terms odd in $\vec{x}$. Continuing we have

$$\langle\phi(t)\vert\hat{x}\vert\phi(t)\rangle = i\int \frac{d^3p}{(2\pi)^3} \left[ {a^{(+)}_{\vec{p}}}^*(t) {\chi... ... \tau_3 \chi^{(+)}(\vec{p}) \vec{\nabla}_{\vec{p}} a^{(+)}_{\vec{p}}(t) \right.$$

$$+ {a^{(-)}_{\vec{p}}}^*(t) {\chi^{(-)}}^\dagger(\vec{p}) \tau_3 \chi^{(-)}(\vec{p}) \vec{\nabla}_{\vec{p}} a^{(-)}_{\vec{p}}(t)$$

$$+ {a^{(-)}_{\vec{-p}}}^*(t) {\chi^{(-)}}^\dagger(\vec{-p}) \tau_3 a^{(+)}_{\vec{p}}(t) \vec{\nabla}_{\vec{p}} \chi^{(+)}(\vec{p})$$

$$+ {a^{(+)}_{\vec{-p}}}^*(t) {\chi^{(+)}}^\dagger(\vec{-p}) \tau_3 a^{(-)}_{\vec{p}}(t) \vec{\nabla}_{\vec{p}} \chi^{(-)}(\vec{p}) \left. \right] ,$$

$$= i\int \frac{d^3p}{(2\pi)^3} \left[ {a^{(+)}_{\vec{p}}}^*(t) {\chi... ...(-it\frac{\vec{p}}{E_p}\right) a^{(+)}_{\vec{p}}(t) \chi^{(+)}(\vec{p}) \right.$$

$$+ {a^{(-)}_{\vec{p}}}^*(t) {\chi^{(-)}}^\dagger(\vec{p}) \tau_3 \left(it\frac{\vec{p}}{E_p}\right) a^{(-)}_{\vec{p}}(t) \chi^{(-)}(\vec{p})$$

$$+ {a^{(-)}_{\vec{p}}}^*(t) {\chi^{(-)}}^\dagger(\vec{p}) \tau_3 \left(-\frac{\vec{p}}{2E_p^2}\right) a^{(+)}_{\vec{p}}(t) \chi^{(-)}(\vec{p})$$

$$+ {a^{(+)}_{\vec{p}}}^*(t) {\chi^{(+)}}^\dagger(\vec{p}) \tau_3 \... ...ec{p}}{2E_p^2}\right) a^{(-)}_{\vec{p}}(t) \chi^{(+)}(\vec{p}) \left. \right] .$$ (4.132)

The first two terms in the last expression above are obtained by noticing that

$$\int \frac{d^3p}{(2\pi)^3} a^{(\pm)^*}_{\vec{p}}(t) \vec{\nabla}_{\vec{p}} a^{(\pm)}_{\vec{p}}(t) = \int \frac{d^3p}{(2\pi)^3} \left[ \mp i t \frac{\vec{p}}{E_p} f^2([\vec{p}-\vec{p}_0]^2) \right.$$

$$+ 2(\vec{p}-\vec{p}_0)f([\vec{p}-\vec{p}_0]^2)f^\prime([\vec{p}-\vec{p}_0]^2) \left. \right] .$$ (4.133)

Since $f([\vec{p}-\vec{p}_0]^2)$ is very narrow, it approxiates a Dirac delta funtion and thus

$$\int \frac{d^3p}{(2\pi)^3} a^{(+)^*}_{\vec{p}}(t) \vec{\nabl... ...a^{(+)}_{\vec{p}}(t) \approx \mp it\frac{\vec{p}_0}{E_{p_0}} .$$ (4.134)

Therefore

$$\langle\phi(t)\vert\vec{x}\vert\phi(t)\rangle = \int \frac{... ...{E_p^2} {a^{(+)}_{\vec{p}}}^*(t)a^{(-)}_{\vec{p}}(t) \right] .$$ (4.135)

The first term represents the expected uniform velocity motion of the wavepacket. In the second term

$${a^{(+)}_{\vec{p}}}^*(t) a^{(-)}_{\vec{p}}(t) \sim e^{2i\vert E_p\vert t}$$ (4.136)

represents a rapid wiggling of the position of the particle about its central location due to the interference of positive- and negative-energy components. This jitter motion is referred to as Zitterbewegung and arises from attempting to localize the particle or from interactions of the particle with a potential.

The positive- and negative-energy components of the wavepacket travel in opposite directions. Thus wavepackets damp out after a time $\Delta t\sim 1/m$ once the interactions with the potential have ceased. An exception is when the potential is very strong. This problem is called the Klein's paradox for reasons which will become apparent in the next section.