Proxy model-based control of complex systems
From a simple RC circuit to complex systems like Internet-of-Things, we see systems, their interconnection, and interaction in the real world. Achieving a reliable
maneuver over its behavior is one of the fundamental problems we deal with in systems and control engineering. Having a reliable system model is central to achieving
this goal. More often than not, developing a physics-based system model is not feasible or computationally too expensive for complex systems.
My research addresses this issue through data-analytics based proxy/surrogate modeling, which are computationally
affordable modeling technique to be used in control and optimization studies.
A complex system is an entity of connected sub-systems exhibiting a collective-dynamics.
The individual sub-systems have their primal behavior, the interconnection among them gives rise to a collective-dynamics as a whole.
 Physics-based first principles models may not be feasible and/or may be computationally too costly to achieve tasks like gradient computation, multi-step ahead forecasting and soft sensor development.
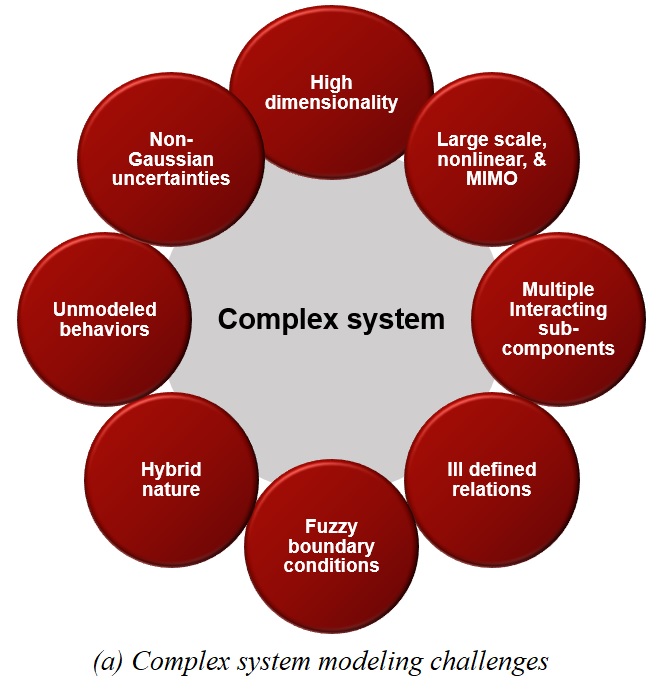
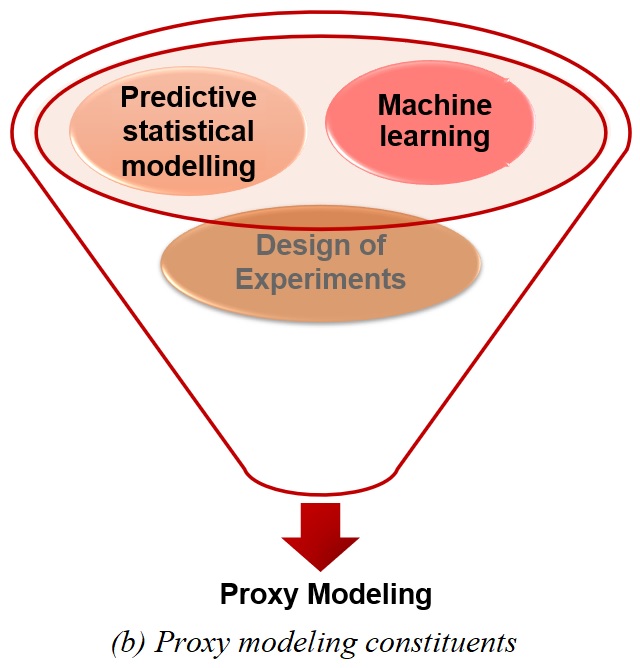
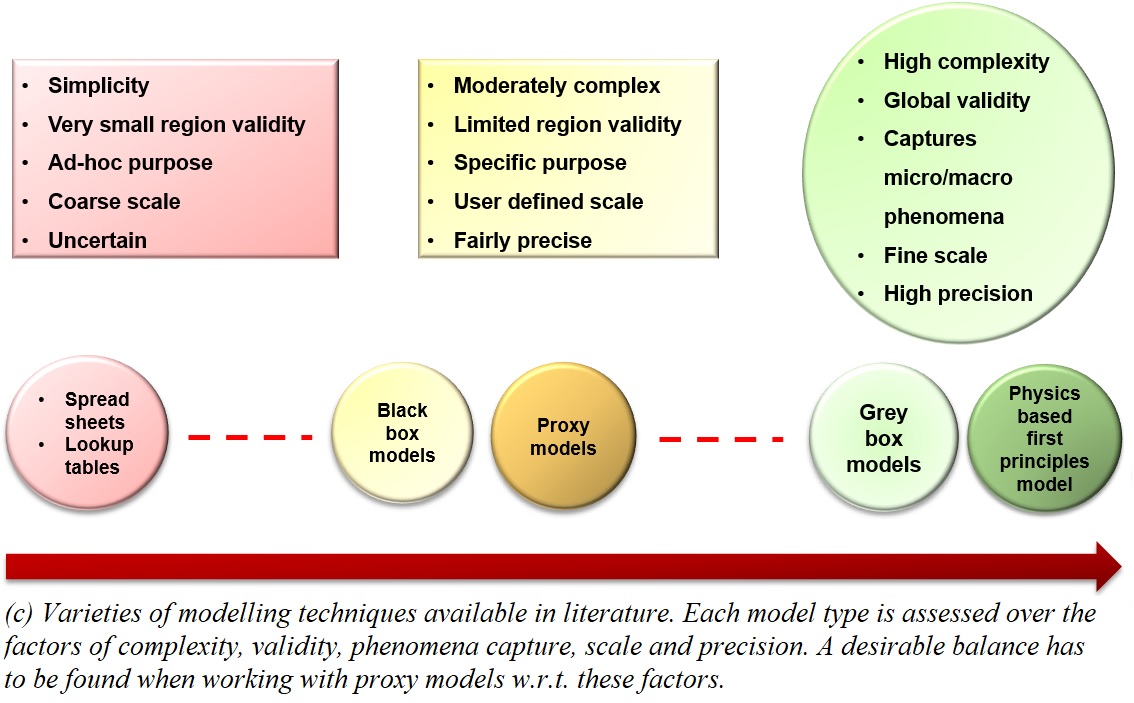
Figure (a) shows some of the challenges faced in working with complex systems. Figure (b) gives a quick glimpse into the techniques that goes into the proxy modeling process. Figure (c) shows the range of system-models varying over varioys factors.
Physics-based models on one end are highly complex but have global validity, captures micro/macro scale phenomena, solvable at any scale with great precision; on the other end, the crude models are highly simple but fails to meet all of these criterion. The
proxy models have to find a 'sweet spot' between these two ends to provide optimal performance with a fair computational cost.
Physics-based first principles models may not be feasible and/or may be computationally too costly to achieve tasks like gradient computation, multi-step ahead forecasting and soft sensor development.
Figure (a) shows some of the challenges faced in working with complex systems. Figure (b) gives a quick glimpse into the techniques that goes into the proxy modeling process. Figure (c) shows the range of system-models varying over varioys factors.
Physics-based models on one end are highly complex but have global validity, captures micro/macro scale phenomena, solvable at any scale with great precision; on the other end, the crude models are highly simple but fails to meet all of these criterion. The
proxy models have to find a 'sweet spot' between these two ends to provide optimal performance with a fair computational cost.
Proxy models are often data driven models, the data can either be obtained through experiments or through a first principle simulator. Proxy models try to capture a particular feature of interest of the system rather than
trying to explain its entire dynamics like a physics based model. Ideally, the experiments / simulations have to be carefully designed such that the resulting data is rich in the information of the interested feature.
Design of experiments, machine learning and statistical modeling techniques forms the core of proxy modeling.
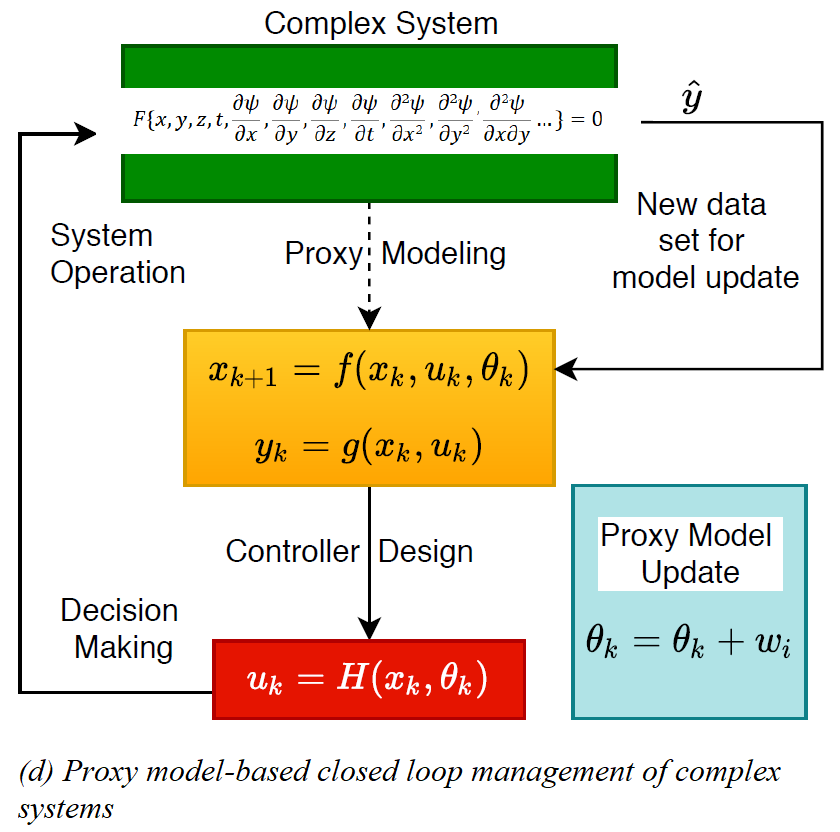
Figure (d) shows the proposed control framework with an optimization objective for managing complex systems. The proxy models developed for the complex system are
used to design a controller that operates the system while optimizing an objective function. The proxy models are calibrated/updated/recomputed when a new set of
measured-data is obtained from the system. Optimization and model calibration alternates throughout the operation of the process. In order to have reliable predictions
from the proxy models, it is important to incorporate the available dynamic input/output data into the model update process.
 https://orcid.org/0000-0002-8055-6273
https://orcid.org/0000-0002-8055-6273