Numerical simulations of torsional oscillations and rigid zonal flows
Torsional oscillations are a 6-7 year timescale azimuthal oscillations of rigid coaxial cylindrical surfaces in the Earth's fluid core (figure 1 below). These oscillations are predicted by theoretical models of the geodynamo, are observed in the geomagnetic field's secular variation, and also explain changes in the length of day observed at the same timescale. They represent one of our most robust link between observation of the dynamics in the core over historical timescales and the balance of forces that is responsible for maintaining the field against decay on geologic timescales. Questions remain concerning the excitation of these waves, and whether they are a fundamental feature of the geodynamo or simply a second order by-product. Also, similar rigid zonal flows at decadal timescale are also detected in both the geomagnetic secular variation (Figure 2) and length of day changes (Figure 3). With my PhD student Colin More, we have shown that decadal fluctuations in the magnetic field inside the core are driven by convective flows and could then force decadal changes in the Lorentz torque. In turn, these changes in the Lorentz torque can generate the observed zonal accelerations.
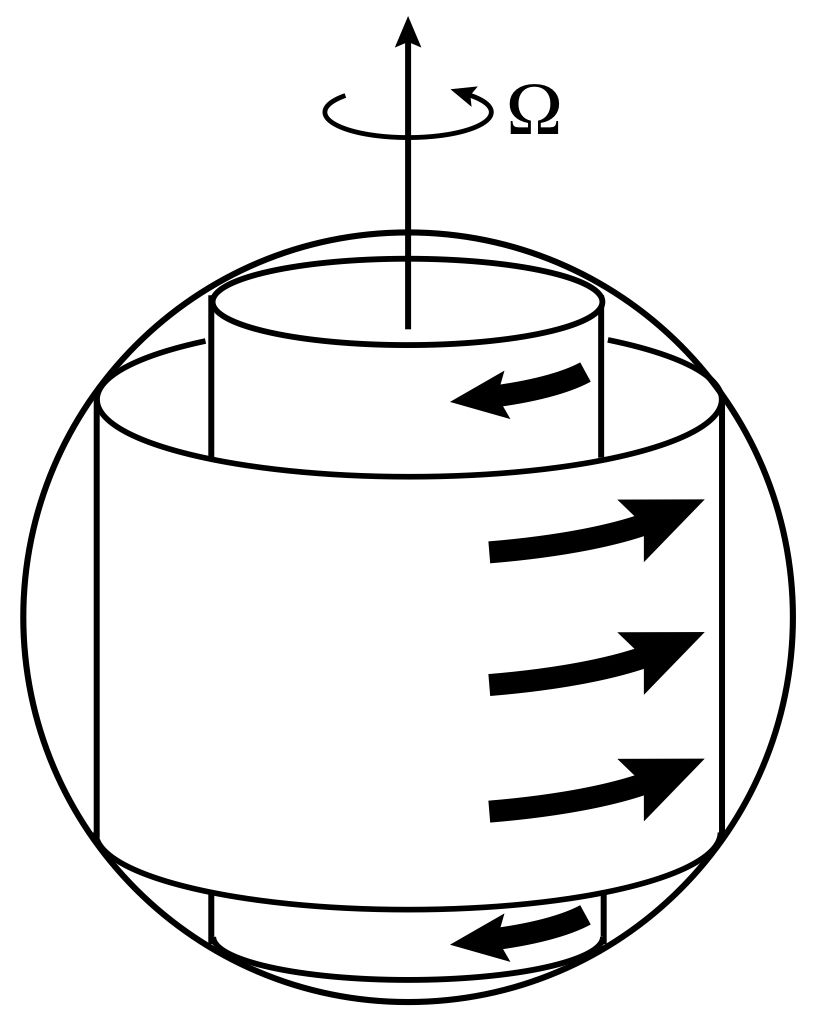
Figure 1: Geometry of rigid zonal flows inside the core. |
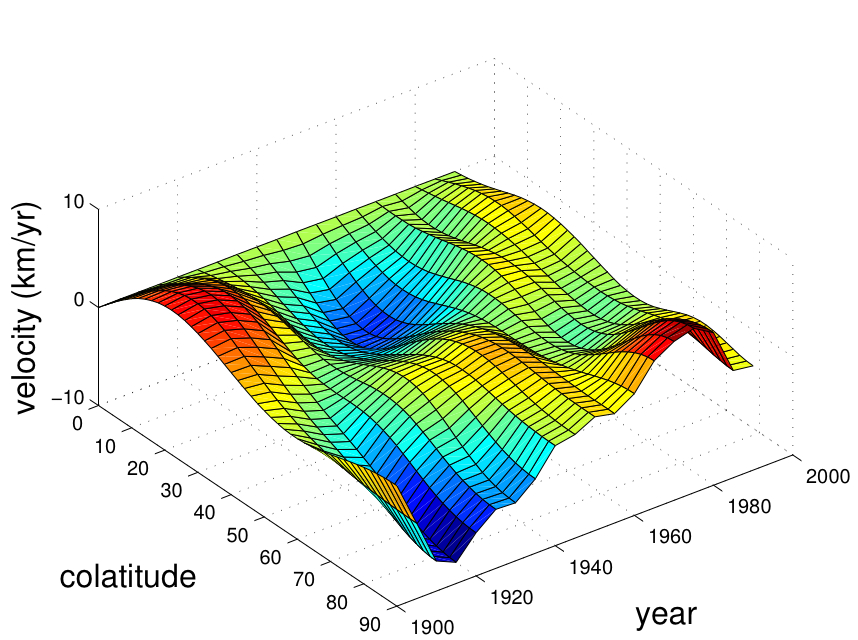
Figure 2: Decadal core zonal motion inferred from geomagnetic secular variation (adapted from Zatman & Bloxham, nature, 1997). |
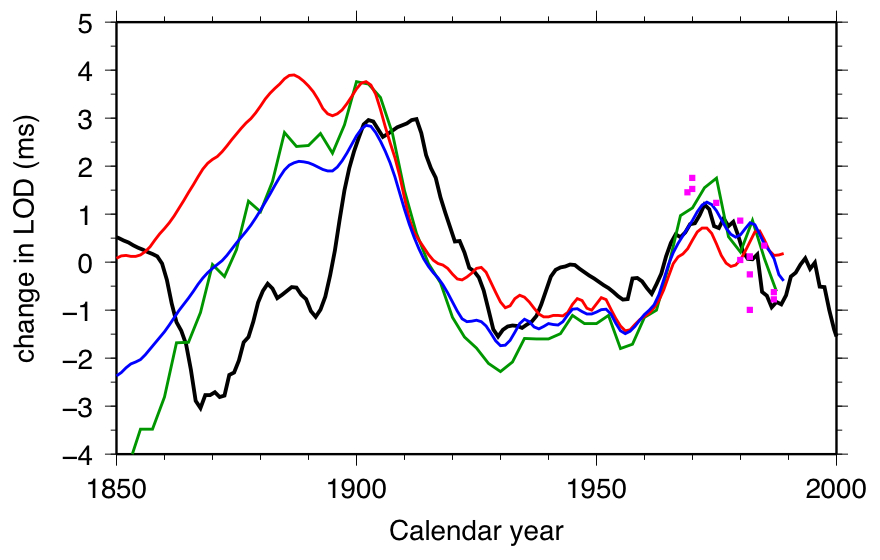
Figure 3: Observed Length of day changes (black) vs predictions (color) based on core flows reconstructed from geomagnetic secular variation. The figure is from Finlay, Dumberry et al, Space Sci. Rev. 2010. |
Some of my papers on this topic
Dumberry, M., 2018, Earth Rotation, Excitation, Core, In: Grafarend E. (eds) Encyclopedia of Geodesy , Encyclopedia of Earth Sciences Series, Springer, Cham.
More, C. and Dumberry, M., 2018, Convectively driven zonal flow accelerations in the Earth's fluid core, Geophysical Journal International, 213, 434-446.
Dumberry, M., 2009, Taylor's constraint and torsional oscillations, Chapter 7 in Les Houches, session LXXXVIII: Dynamos . Editors P. Cardin and L. F. Cugliandolo, Elsevier, p383-401.
Dumberry, M. and Mound, J. 2008, Constraints on core-mantle electromagnetic coupling from torsional oscillations normal modes, J. Geophys. Res., 113, B03102.
Dumberry, M., 2007, Torsional oscillations, in Encyclopedia of Geomagnetism and Paleomagnetism, Gubbins, D. and Herrero-Bervera, E. Eds., Springer, Dordrecht, The Netherlands, pp. 746-748.
Dumberry, M. and Bloxham, J., 2004, Variations in the Earth's gravity field caused by torsional oscillations in the core, Geophys. J. Int., 159, 417-434.
Dumberry, M. and Bloxham, J., 2003, Torque balance, Taylor's constraint and torsional oscillations in a numerical model of the geodynamo, Phys. Earth Planet. Inter., 140, 29-51.

