bio photo

Mathieu Dumberry

email: dumberry@ualberta.ca

Professor

Department of Physics
University of Alberta
Edmonton, AB
T6G 2E1
Canada
Office: CCIS 3-093

The Cassini state of the Moon

It is well known that the reason we see only one face of the Moon is because it's rotation is tidally locked: its revolution period around Earth is equal to the period of the Moon's rotation around itself. Yet, as the video below shows (credit: NASA), we see a little bit more than one half of its surface during a full cycle of full-to-new Moon.



The reason for this has to do with the geometry of the lunar orbit and its rotation vector. The plane of the Moon's orbit is inclined by 5.14o with respect to the normal to the ecliptic plane - the plane about which Earth rotates around the Sun. But just like the Earth’s rotation axis is inclined by 23.5o in space, the Moon’s rotation axis is also inclined, by about 1.54o in space. The tilt of the rotation axis and the tilt of the orbital plane are co-planar with the ecliptic normal, a confiugration known as a Cassini state, named after the seventeenth century Italian astronomer. The animation below shows the geometry (not to scale) of the orbit and rotation of the Moon (credit: Christopher Stys). The grey plane is the ecliptic plane. The yellow axis is the normal to this plane. The inclined orbit takes the Moon above and below the ecliptic plane. The blue axis is in the direction normal to the plane of the Moon's orbit. The red axis is the direction of the rotation axis of the Moon: over the course of one Lunar orbit, it points in the same direction in space. The red, yellow and blue axes remain on the same plane, and this defines a Cassini state. The green axis is the direction of the minimum moment of inertia: it points generally towards the Earth, but its direction changes over the course of one orbit, which is part of the reason for the optical libration in the animation above.



Now, just as the Earth's spin axis is precessing in space like a spinning top with a period of 26 000 yrs, the Cassini plane of the Moon is also precessing, but with a period of 18.6 years. This precession is forced by the precession of the plane of the Lunar orbit at the same period.

Like the Earth, the Moon is suspected to have a metallic iron core, its outer region being fluid but the central part being solid. This means that the spin vector of the Moon that is depicted in the animations above only pertains to the spin of its outer solid shell - its mantle and crust. The solid inner core is also expected to be in a Cassini state, so its spin vector is expected to lie in the same plane as the spin vector of the mantle, but its angle can be different. In a recent study with MSc student Christopher Stys, we calculated the tilt of the spin axis of this solid inner core so that it obeys a Cassini state. The tilt angle depends on the the deep interior structure on the Moon, in particular it depends on the frequency of the free inner core nutation (Figure 1). We determined that the inner core is tilted as much as 17o away from the mantle in one direction or 33o away in the other (Figure 2). Our model of the rotational dynamics of the Moon is the first to fully take into account the presence of a solid inner core. The differential rotation between the solid inner core and fluid core may have contributed in the past to the generation of its magnetic field by dynamo action.

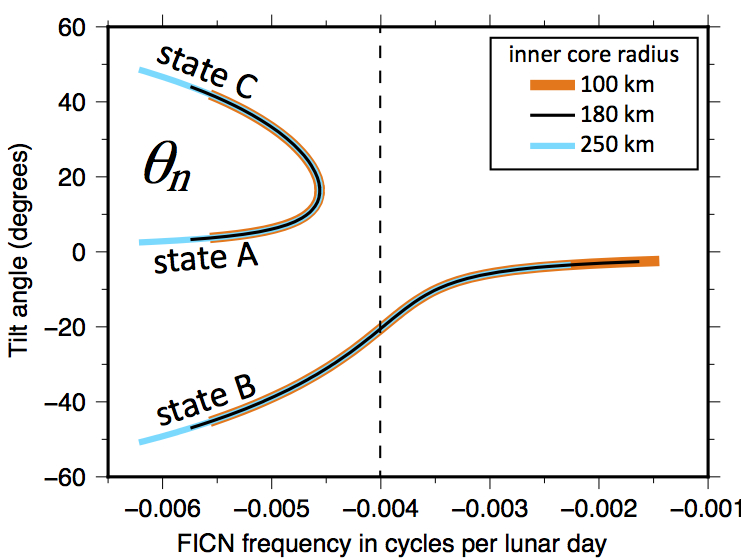
Figure 1: The tilt angle of the inner core as a function of the free inner core nutation frequency. Figure taken from Stys & Dumberry, JGR, 2018.

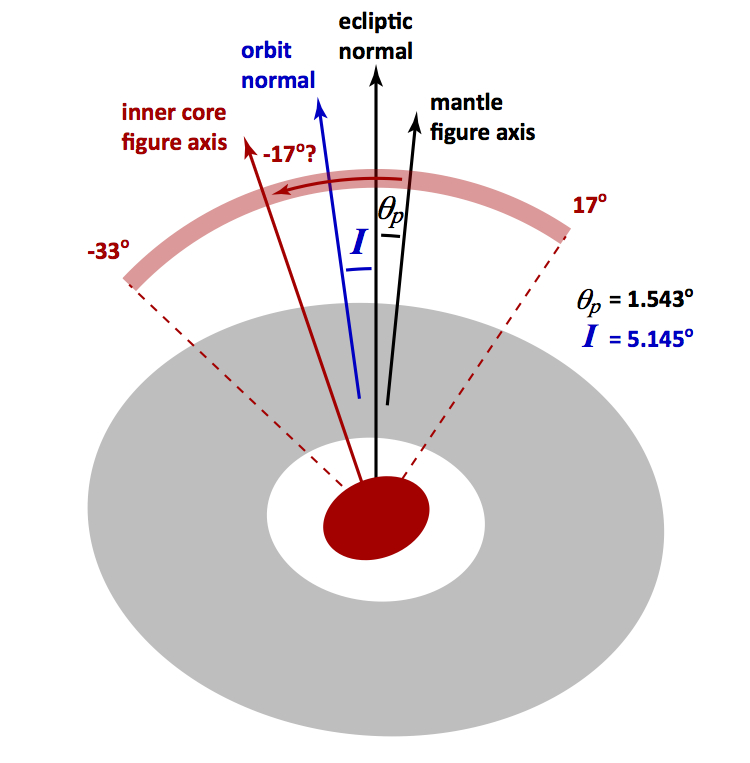
Figure 2: The Cassini state of the inner core. The red shaded arc shows the possible range of inner core precession angles, from 17o to -33o, measured with respect to the mantle figure axis. Adopting a Lunar interior density model close to that of Matssuyama et al. GRL, 2016 gives a precession angle of -17o. Angles, ellipticities and region thicknesses are not drawn to scale. Figure taken from Stys & Dumberry, JGR, 2018.

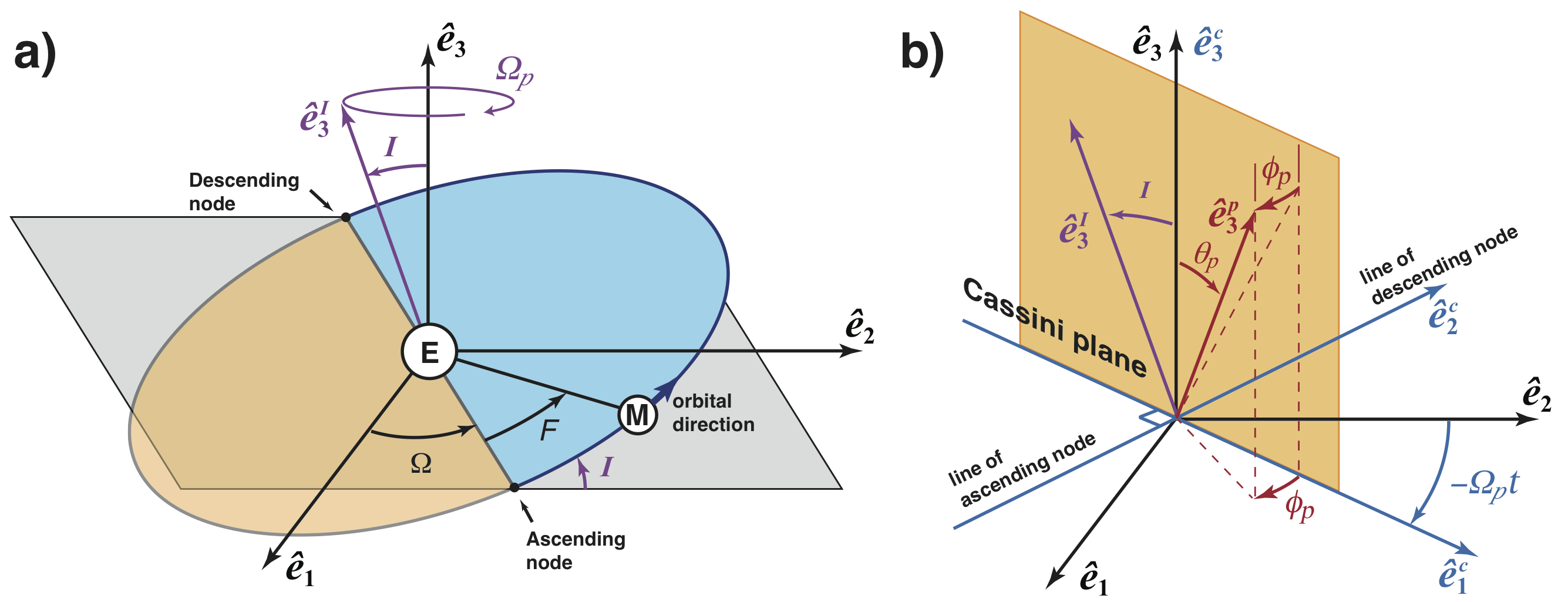
Precise observations of the lunar rotation have revealed that the spin axis of the Moon does not lie exactly on the plane formes by the ecliptic and orbit normals, but is a little bit ahead by a phase lead of 0.27 arcsec (Figure 3). This indicates that a part of the rotational energy of the Moon is dissipated. Possible mechanisms that can explain this phase lead include the delayed response of a deformable “soft” mantle to tidal forces, viscous friction at the core-mantle boundary and the inner core boundary, and also from viscous deformations within the solid inner core.

Figure 3: (a) The orbit of the Moon (M) around Earth (E) as seen in the inertial frame and (b) the Cassini state of the Moon. As a result of dissipation, the spin axis of the Moon (unit vector e3p is ahead of the Cassini plane by an angle φ p = 0.27 arcsec. Figure taken from Organowski & Dumberry, JGR, 2020.

Some of my papers on this topic

  • Zhang, J. and Dumberry, M., 2021, Viscous dissipation in the fluid core of the Moon, Journal of Geophysical Research: Planets, 126, e2021JE006966.

  • Organowski, O. and Dumberry, M., 2020, Viscoelastic relaxation within the Moon and the phase lead of its Cassini state, Journal of Geophysical Research: Planets, 125, e2020JE006386.

  • Stys, C. and Dumberry, M., 2020, A past lunar dynamo thermally driven by the precession of its inner core, Journal of Geophysical Research: Planets, 125, e2020JE006396.

  • Stys, C. and Dumberry, M., 2018, The Cassini state of the Moon's inner core, Journal of Geophysical Research: Planets, 123, 2868-2892.

  • Dumberry, M. and Wieczorek, M. A., 2016, The forced precession of the Moon's inner core, Journal of Geophysical Research: Planets, 121, 1264-1292.