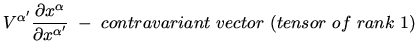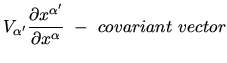Tensor transformation rules

Tensors are defined by their transformation properties under coordinate change. One distinguishes covariant and contravariant indexes. Number of indexes is tensor's rank, scalar and vector quantities are particular case of tensors of rank zero and one.

Consider coordinate change 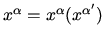$x^{\alpha} = x^{\alpha}(x^{\alpha^\prime})$. Transformation rules are

Scalar

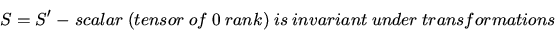$$S = S^\prime  -  scalar (tensor of 0 rank) is invariant under transformations$$ (6)

Vector

$$V^{\alpha} = V^{\alpha^\prime} \frac{\partial x^\alpha}{\partial x^{\alpha^\prime}} - contravariant vector (tensor of rank 1)$$ (7)

$$V_\alpha = V_{\alpha^\prime} \frac{\partial x^{\alpha^\prime}}{\partial x^\alpha} - covariant vector$$ (8)

Tensor

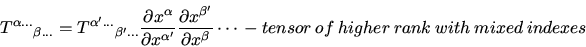$${T^{\alpha \ldots}}_{\beta \ldots} = {T^{\alpha^\prime \ldo... ...al x^\beta} \cdots  - tensor of higher rank with mixed indexes$$ (9)

In general, the position of the indexes matters. Above case where all covariant indexes are at the end is a special case.

Contraction

Contraction is a summation over a pair of one covariant and one contravariant indexes. It creates a tensor of rank less than original by two. We use shorthand that when two indexes of different type are labeled by the same latter it implies a summation over them.

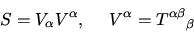$$S=V_{\alpha} V^{\alpha},     V^\alpha = {T^{\alpha\beta}}_{\beta}$$ (10)