


Next: Tensor transformation rules
Up: geom_formulas
Previous: General notation
Coordinate transformation is given by the set of functions
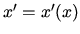 . It is often convenient
to add prime to the index, i.e write
. It is often convenient
to add prime to the index, i.e write
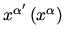 .
This way
.
This way 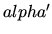 not only means that the vector is considered
in other frame, but also
not only means that the vector is considered
in other frame, but also 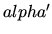 being different index than
being different index than 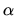 we save on Greek letters. Otherwise we would have to write
we save on Greek letters. Otherwise we would have to write
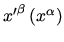 to designate the dependence of
to designate the dependence of 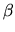 primed coordinate
on
primed coordinate
on 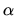 original one. This is especially useful for differentiation,
so we can write
original one. This is especially useful for differentiation,
so we can write
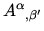 to say the
to say the 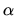 's component
of vector A in original frame is differentiated wrt to
's component
of vector A in original frame is differentiated wrt to 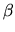 coordinate
in another, primed, system.
coordinate
in another, primed, system.
We consider coordinate transformation invertible, i.e., there exist the inverse
functions
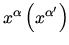 . In this case, using
chain differentiation rule
. In this case, using
chain differentiation rule
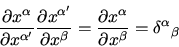 |
(4) |
the latter step following from condition that coordinates in the same system
are independent on each other.
Similarly,
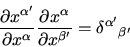 |
(5) |
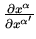 can be viewed as
square matrices, but they are not tensors, since they are not objects defined
in one particular coordinate system (actually they mix two coordinate systems).
Coordinates
can be viewed as
square matrices, but they are not tensors, since they are not objects defined
in one particular coordinate system (actually they mix two coordinate systems).
Coordinates 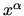 's themselves do not constitute a vector,
and when they are viewed as functions of another coordinate set,
the transformation matrix is build from usual derivatives
of these functions wrt their arguments. Quite similar with what you have to
deal with when, for example, you change variables in a multidimensional integral.
's themselves do not constitute a vector,
and when they are viewed as functions of another coordinate set,
the transformation matrix is build from usual derivatives
of these functions wrt their arguments. Quite similar with what you have to
deal with when, for example, you change variables in a multidimensional integral.



Next: Tensor transformation rules
Up: geom_formulas
Previous: General notation
Dmitri Pogosyan
2009-10-23
![]() . In this case, using
chain differentiation rule
. In this case, using
chain differentiation rule
![]() can be viewed as
square matrices, but they are not tensors, since they are not objects defined
in one particular coordinate system (actually they mix two coordinate systems).
Coordinates
can be viewed as
square matrices, but they are not tensors, since they are not objects defined
in one particular coordinate system (actually they mix two coordinate systems).
Coordinates ![]() 's themselves do not constitute a vector,
and when they are viewed as functions of another coordinate set,
the transformation matrix is build from usual derivatives
of these functions wrt their arguments. Quite similar with what you have to
deal with when, for example, you change variables in a multidimensional integral.
's themselves do not constitute a vector,
and when they are viewed as functions of another coordinate set,
the transformation matrix is build from usual derivatives
of these functions wrt their arguments. Quite similar with what you have to
deal with when, for example, you change variables in a multidimensional integral.