


Next: Coordinate transformations
Up: geom_formulas
Previous: geom_formulas
We use Greek letters
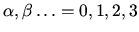 for components of 4-vectors,tensors, etc and Roman letters
for components of 4-vectors,tensors, etc and Roman letters
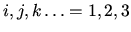 for their spatial components.
Ordinary partial derivative with respect to coordinate
for their spatial components.
Ordinary partial derivative with respect to coordinate 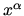 is
often denoted by comma
is
often denoted by comma
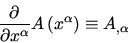 |
(1) |
Up or down position of the index after comma is generally important.
We often differentiate with respect to vectors (note, coordinates 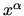 themselves do not constitute vectors) or even tensors, for example,
the Lagrangian density
themselves do not constitute vectors) or even tensors, for example,
the Lagrangian density
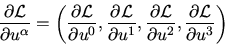 |
(2) |
Note, that it matters, whether one differentiate with respect to covariant
or contravariant components, i.e
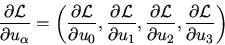 |
(3) |
is a different object. We always write the derivatives with respect to vectors
explicitly. One needs some care with notation when the vector
that we differentiate with respect to is itself the gradient
of a scalar function. Then we get the notation like
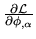 which means
which means
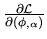 .
.



Next: Coordinate transformations
Up: geom_formulas
Previous: geom_formulas
Dmitri Pogosyan
2009-10-23
![]() themselves do not constitute vectors) or even tensors, for example,
the Lagrangian density
themselves do not constitute vectors) or even tensors, for example,
the Lagrangian density