


Next: The metric tensor
Up: geom_formulas
Previous: Tensor transformation rules
There are two special tensors, which components are invariant under
arbitrary coordinate transformations.
The first one is rank-2 unit tensor
that is represented by the unit matrix
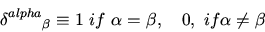 |
(11) |
which is often called Kronecker symbol. Note that it has mixed components.
One may encounter
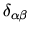 which in some coordinate system
is represented by unit matrix, but such tensor will have its components changed
in another frame (check !).
The effect of contraction of the Kronecker symbol with another vector is
the replacement of the component index
which in some coordinate system
is represented by unit matrix, but such tensor will have its components changed
in another frame (check !).
The effect of contraction of the Kronecker symbol with another vector is
the replacement of the component index
 |
(12) |
The second special tensor has rank equal to dimensionality  of the space,
and is defined as
of the space,
and is defined as
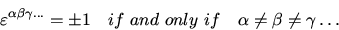 |
(13) |
with
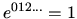 and changing sign with each permutation of a pair of
indexes. Thus,
and changing sign with each permutation of a pair of
indexes. Thus,
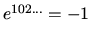 , etc. This tensor is known as
fully antisymmetric tensor of rank
, etc. This tensor is known as
fully antisymmetric tensor of rank 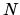 or Levi-Civita symbol.
With its help one can define a dual tensor to any fully antisymmetric
tensor of rank
or Levi-Civita symbol.
With its help one can define a dual tensor to any fully antisymmetric
tensor of rank 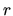 less than
less than 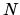 . Such dual tensor will have rank
. Such dual tensor will have rank 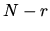 .
For example in 4D if
.
For example in 4D if
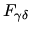 is antisymmetric, its dual is
is antisymmetric, its dual is
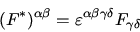 |
(14) |
while for a tensor of rank 3, the dual will be a vector
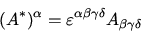 |
(15) |



Next: The metric tensor
Up: geom_formulas
Previous: Tensor transformation rules
Dmitri Pogosyan
2009-10-23
![]() of the space,
and is defined as
of the space,
and is defined as