


Next: Affine connection (Christoffel symbols)
Up: geom_formulas
Previous: Tensor transformation rules
- Definition
- The metric tensor
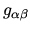 specifies the invariant interval
(distance) between two neighbouring points (events)
specifies the invariant interval
(distance) between two neighbouring points (events)
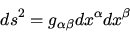 |
(6) |
- Lowering of indexes
-
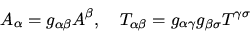 |
(7) |
- Defining
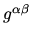
-
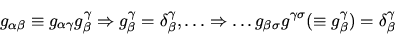 |
(8) |
- Rising of indexes
-
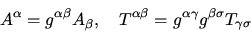 |
(9) |
Dmitri Pogosyan
2006-09-28