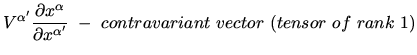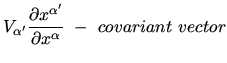Tensor transformation rules

Tensors are defined by their transformation properties under coordinate change. One distinguishes convariant and contravariant indexes. Number of indexes is tensor's rank, scalar and vector quantities are particular case of tensors of rank zero and one.

Consider coordinate change 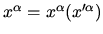$x^{\alpha} = x^{\alpha}(x^{\prime \alpha})$. Transformation rules are

Scalar

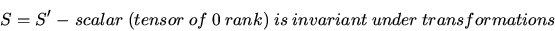$$S = S^\prime ~ -~ scalar~(tensor~of~0~rank)~is~invariant~under~transformations$$ (1)

Vector

$$V^{\alpha} = V^{\alpha^\prime} \frac{\partial x^\alpha}{\partial x^{\alpha^\prime}}~-~contravariant~vector~(tensor~of~rank~1)$$ (2)

$$V_\alpha = V_{\alpha^\prime} \frac{\partial x^{\alpha^\prime}}{\partial x^\alpha}~-~covariant~vector$$ (3)

Tensor

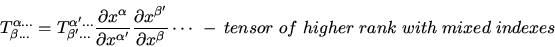$$T^{\alpha \ldots}_{\beta \ldots} = T^{\alpha^\prime \ldots}_... ...al x^\beta} \cdots ~-~tensor~of~higher~rank~with~mixed~indexes$$ (4)

Contraction

Contraction is a summation over a pair of one covariant and one contravariant indexes. It creates a tensor of rank less than original by two. We use shorthand that when two inderxes of different type are labeled by the same latter it implies a summation over them.

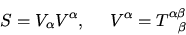$$S=V_{\alpha} V^{\alpha}, ~~~~ V^\alpha = T^{\alpha\beta}_{~~\beta}$$ (5)