Our goal is to investigate the differential equation which defines
![]() , and in particular to solve for
, and in particular to solve for ![]() explicitly, so that the
expansion for
explicitly, so that the
expansion for ![]() can be explicitly carried out.
From Huygens' principle,
can be explicitly carried out.
From Huygens' principle,
| (6.28) |
A form valid for all time is
Using the chain rule and the fact that
![]() satisfies the
Schrödinger equation, we have
satisfies the
Schrödinger equation, we have
| (6.30) |
Since
| (6.31) |
we have
| (6.32) |
Substituting equation 6.29 for
![]() , we have
, we have
| (6.33) |
Therefore
| (6.34) |
is the Green's function equation in the Schrödinger theory.
Along with the boundary conditions
![]() for
for ![]() this defines the retarded Green's function.
this defines the retarded Green's function.
For the free-particle propagator
![]() .
.
![]() can depend only upon the difference of the
coordinates
can depend only upon the difference of the
coordinates
![]() and
and ![]() .
This is because the wave at
.
This is because the wave at
![]() emerging from
a unit source at
emerging from
a unit source at ![]() which is turned on at
which is turned on at ![]() depends only on
the interval
depends only on
the interval
![]() , and
, and
![]() is precisely the amplitude of this wave.
is precisely the amplitude of this wave.
Consider the Fourier transform
| (6.35) |
The Schrödinger equation for the Green's function becomes
| (6.36) |
and hence for
![]() ,
,
| (6.37) |
To complete the expression, we must have a rule for handling the singularity. We will see that the retarded boundary condition
| (6.38) |
requires us to add a positive infinitesimal imaginary part to the denominator. Lets integrate
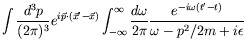 |
|||
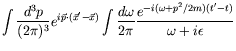 |
|||
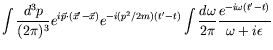 |
(6.39) |
The integral over ![]() is evaluated as a contour integral in the
complex
is evaluated as a contour integral in the
complex ![]() -plane as shown in figure 6.3.
For
-plane as shown in figure 6.3.
For ![]() , the contour may be closed along an infinite
semicircle below the real axis in order to ensure exponential damping
of the integrand, and the value of the integral is
, the contour may be closed along an infinite
semicircle below the real axis in order to ensure exponential damping
of the integrand, and the value of the integral is ![]() by Cauchy's
theorem.
For
by Cauchy's
theorem.
For ![]() , the contour is closed above and the integral
vanishes because the pole at
, the contour is closed above and the integral
vanishes because the pole at ![]() lies outside the contour.
The integral is thus just
lies outside the contour.
The integral is thus just ![]() times the step function.
Continuing our previous integration, we have
times the step function.
Continuing our previous integration, we have
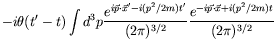 |
|||
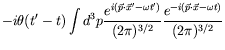 |
|||
| (6.40) |
where the subscript ![]() stands for plane waves.
This is a special case for plane waves.
In general
stands for plane waves.
This is a special case for plane waves.
In general
where ![]() is a generalized sum and integral over the spectrum of
quantum numbers
is a generalized sum and integral over the spectrum of
quantum numbers ![]() ,
, ![]() is a complete set of normalized
solutions to the Schrödinger equation which satisfy a completeness
statement
is a complete set of normalized
solutions to the Schrödinger equation which satisfy a completeness
statement
| (6.42) |
There is an enormous amount of information contained in
![]() .
All the solutions of the Schrödinger equation, including the bound
states, as required in the completeness relation, appear with equal
weight.
It is no wonder that
.
All the solutions of the Schrödinger equation, including the bound
states, as required in the completeness relation, appear with equal
weight.
It is no wonder that ![]() is difficult to compute.
is difficult to compute.
The same Green's function which propagates a solution of the Schrödinger equation forward in time propagates its complex conjugate backward in time. From (6.41) we have
| (6.43) |
and
| (6.44) |