Charge Conjugation

Charge conjugation is a new symmetry in nature. To each particle there is an antiparticle and, in particular, the existence of electrons implies the existence of positrons. In the hole theory, the absence of an energy $-E$ and the absence of a charge $-e$, is equivalent to the presence of a positron of positive energy $+E$ and charge $+e$. For an electron of negative energy

$$(i\not{\;\!\!\!\partial}- e\not{\!\!A}-m)\psi = 0 .$$ (5.233)

For a positron, $\psi_C$, with positive energy

$$(i\not{\;\!\!\!\partial}+ e\not{\!\!A}-m)\psi_C = 0 .$$ (5.234)

We look for an operator transforming the two equations into each other. Taking the complex conjugate of the Dirac equation, multiplying by $-1$, and remembering that $A_\mu$ is real, we have

$$\left[ \left( i\frac{\partial}{\partial x^\mu} + eA_\mu \right) (\gamma^\mu)^*+ m \right] \psi^* = 0.$$ (5.235)

We look for a nonsingular matrix, $C\gamma^0$, such that

$$(C\gamma^0)(\gamma^\mu)^*(C\gamma^0)^{-1} = -\gamma^\mu .$$ (5.236)

If this is the case, we have

$$(i\not{\;\!\!\!\partial}+ e\not{\!\!A}- m)(C\gamma^0\psi^*) = 0,$$ (5.237)

with

$$C\gamma^0\psi^* = C (\psi^\dagger\gamma^0)^T = C\overline{\psi}^T$$ (5.238)

being the positron wave function. In our representation we can see that

$$\gamma^0(\gamma^\mu)^*\gamma^0 = (\gamma^\mu)^T ,$$ (5.239)

or explicitly

$$\textrm{for}\ \mu = i, \quad \gamma^0(\gamma^i)^*\gamma^0 = \gamma^0(\gamma^i\gamma^0)^* = -\g... ...\gamma^0(\gamma^i)^* = - (\gamma^i)^* = ({\gamma^i}^\dagger)^* = (\gamma^i)^T ,$$

$$\textrm{for}\ \mu = 0, \quad \gamma^0(\gamma^0)^*\gamma^0 = \gamma^0 = (\gamma^0)^T .$$

Therefore

$$(C\gamma^0)(\gamma^\mu)^*(C\gamma^0)^{-1} = C(\gamma^0{\gamma^\mu}^*\gamma^0)C^{-1} = C(\gamma^\mu)^T C^{-1} = -\gamma^\mu$$ (5.240)

or

$$C^{-1}\gamma^\mu C = - (\gamma^\mu)^T.$$ (5.241)

Since

$$\left. (\gamma^\mu)^T = \right\{ \begin{array}{r} \gamma^\mu... ...2 \\ -\gamma^\mu \quad\textrm{for}\quad \mu=1,3 \end{array} ,$$ (5.242)

$C$ must commute with $\gamma^1$ and $\gamma^3$, and anti-commute with $\gamma^0$ and $\gamma^2$. Therefore we try

$$\fbox{$\displaystyle C=i\gamma^2\gamma^0 $}$$ (5.243)

and see

$$C^{-1} = i\gamma^0\gamma^2 = -i\gamma^2\gamma^0 = -C ,$$ (5.244)

$$C^\dagger = -i\gamma^0(\gamma^2)^\dagger = i\gamma^0\gamma^2 = -i\gamma^2\gamma^0 = -C ,$$ (5.245)

$$C^T = i(\gamma^0)^T(\gamma^2)^T = i\gamma^0\gamma^2 = -i\gamma^2\gamma^0 = -C .$$ (5.246)

It suffices to be able to construct a matrix $C$ in any given representation since a unitary transformation to any other representation when applied to this $C$ will give a matrix appropriate to the new representation. We note also that there is a phase arbitrariness in our definition of $C$. We thus have the charge conjugate solution

$$\psi_C = C\overline{\psi}^T = C\gamma^0\psi^* = i\gamma^2\gamma^0\gamma^0\psi^* = i\gamma^2\psi^* .$$ (5.247)

Lets consider an example. For a negative-energy electron at rest with spin down.

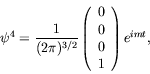$$\psi^4 = \frac{1}{(2\pi)^{3/2}} \left( \begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \end{array}\right) e^{imt},$$ (5.248)

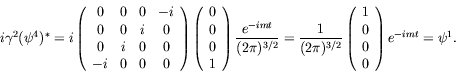$$i\gamma^2(\psi^4)^* = i \left( \begin{array}{cccc} 0 & 0 & 0... ...ay}{c} 1 \\ 0 \\ 0 \\ 0 \end{array}\right) e^{-imt} = \psi^1.$$ (5.249)

The absence of a spin-down negative-energy electron at rest is equivalent to the presence of a spin-up positive-energy positron at rest.

Noticing $[C,\gamma_5]=i(\gamma^2\gamma^0\gamma^5 - \gamma^5\gamma^2\gamma^0)=0$ and recalling that $\gamma_5^\dagger=\gamma_5=\gamma_5^*$, we applying the transformation to an arbitrary spin-momentum eigenstate, $\psi$,

$$\psi_C = C\overline{\psi}^T = C\gamma_0\psi^* = C\gamma_0 \left( \frac{\epsilon\not{p} + m}{2m} \right)^* \left( \frac{1 + \gamma_5\not{s}}{2} \right)^* \psi^*$$

$$= C \left( \frac{\epsilon\gamma_0\not{p}^*\gamma_0 + m}{2m} \right) \left( \frac{1 + \gamma_0\gamma_5\not{s}^*\gamma_0}{2} \right) \gamma_0 \psi^*$$

$$= C \left( \frac{\epsilon\not{p}^T + m}{2m} \right) \left( \frac{1 - \gamma_5\not{s}^T}{2} \right) \gamma_0 \psi^*$$

$$= \left( \frac{-\epsilon\not{p} + m}{2m} \right) \left( \frac{1 + \gamma_5\not{s}}{2} \right) C\gamma_0 \psi^*$$

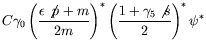$$= \left( \frac{-\epsilon\not{p} + m}{2m} \right) \left( \frac{1 + \gamma_5\not{s}}{2} \right) \psi_C .$$ (5.250)

We see that the operation yields from a negative-energy solution described by 4-vector $p_\mu$ and polarization $s_\mu$, a positive-energy solution with the same $p_\mu$ and $s_\mu$.

In terms of free-particle spinors

$$C\overline{u}^T(p,s) = e^{i\phi(p,s)} v(p,s) ,$$ (5.251)

$$C\overline{v}^T(p,s) = e^{i\phi(p,s)} u(p,s) .$$ (5.252)

Therefore $v(p,s)$ and $u(p,s)$ are charge-conjugate spinors, within a phase factor of $\phi(p,s)$. Notice that $s$ does not change sign under charge conjugation but the spin does reverse.

The operator $\psi_C=C\overline{\psi}^T$ explicitly constructs the wave function of a positron. We may develop from it an invariance operation for the Dirac equation by defining the additional operator which changes the spin of the electromagnetic field. The instructions for this operator are:

1. take complex conjugate,
2. multiply by $C\gamma_0$,
3. replace $A_\mu$ by $-A_\mu$.

This is a formal symmetry of the Dirac theory. it transforms the Dirac equation for an electron into the same equation for a positron and is called the charge conjugation transformation $\mathcal{C}$.

$\mathcal{C}$ describes a particle with the same mass and spin direction, but with opposite charge, opposite sign of energy and opposite sign of momentum. Both $\psi$ and $\psi_C$ propagate forward in time. If a spin-1/2 particle is its own anti-particle, it is a ``Marjoriana fermion''. The neutrino is the only possible candidate for such a particle from the known elementary particles.