Wave Equation for a Spin-0 Particle

The simplest physical system is an isolated free particle. The nonrelativistic Hamiltonian for such a system is

$$H = \frac{\vec{p}^{\: 2}}{2m}.$$ (4.1)

In operator form, we write

$$H \rightarrow \hat{E}\equiv i\hbar\frac{\partial}{\partial t} ,$$ (4.2)

$$\vec{p} \rightarrow \hat{p}\equiv -i\hbar\vec{\nabla} .$$ (4.3)

When operating on a wave-function, $\psi(\vec{x},t)$, we have

$$\hat{E} \psi(\vec{x},t) = \frac{\hat{p}^2}{2m}\psi(\vec{x},t)$$ (4.4)

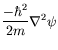$$i\hbar\frac{\partial\psi}{\partial t} = \frac{-\hbar^2}{2m}\nabla^2\psi$$ (4.5)

which is the familiar Schrödinger equation.

The left- and right-hand sides of the Schrödinger equation transform differently under a Lorentz transformation. To circumvent this problem, it is natural to try the Hamiltonian of a relativistic free particle,

$$H = \sqrt{\vec{p}^{\: 2}c^2+m^2c^4} .$$ (4.6)

In terms of operators, we can write

$$i\hbar\frac{\partial\psi}{\partial t} = \sqrt{-\hbar^2 c^2\nabla^2+m^2c^4}\ \psi .$$ (4.7)

You might wonder how the square-root operator can be interpreted? If we expand it, we obtain all powers of the gradient operator and his will lead to a non-local theory. In addition, relativistic invariance is not clearly exhibited since there is a lack of symmetry between the space and time coordinates.

We can avoid these difficulties by starting with the square of the Hamiltonian and thus removing the square-root:

$$H^2 = \vec{p}^{\: 2}c^2 + m^2 c^4.$$ (4.8)

This relation is equivalent to $H=\pm\sqrt{\vec{p}^{\: 2}c^2+m^2c^4}$. We will see later that the negative sign will give rise to solutions of negative energy which at first sight have no physical significance. By squaring the Hamiltonian we have thus introduce an extraneous solution with negative energy. After some hindsight, we will see that the negative-energy solution is capable of physical interpretation in the terms of an antiparticle.

Applying the operator form of equation 4.8 to a wave-function we obtain

$$-\hbar^2\frac{\partial^2\psi}{\partial t^2} = \left(-\hbar^2c^2\nabla^2+m^2c^4\right)\psi ,$$ (4.9)

$$\frac{1}{c^2}\frac{\partial^2\psi}{\partial t^2} - \nabla^2\psi + \frac{m^2c^2}{\hbar^2}\psi = 0 ,$$

$$\frac{\partial^2\psi}{\partial (x^0)^2}-\frac{\partial^2\psi}{\partial (x^k)^2} + \frac{m^2c^2}{\hbar^2}\psi = 0 ,$$

$$\left( \Box + \frac{m^2c^2}{\hbar^2} \right) \psi = 0 .$$ (4.10)

Taking $c=\hbar\equiv 1$ we obtain

$$\fbox{$ \displaystyle (\Box + m^2)\psi = 0 $}\ ,$$ (4.11)

which is the Klein-Gordon equation.