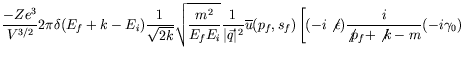- Show that the plane-wave solutions normalized as
have the desired Lorentz transformation properties.
In particular, include the effect of a Lorentz transformation on the
box volume  to show that
to show that
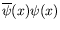 is a scalar
and that
is a scalar
and that
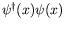 is the time component of a vector,
as desired.
is the time component of a vector,
as desired.
- Prove the following:
-
![$\textrm{Tr}[\gamma_5\not{a}\not{b}] = 0$](img4848.png) ,
,
-
![$\textrm{Tr}[\gamma_5\not{a}\not{b}\not{c}\not{d}] =
4i\epsilon_{\alpha\beta\gamma\delta}a^\alpha b^\beta c^\gamma
d^\delta$](img4849.png) ,
,
-
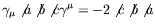 ,
,
-
![$\gamma_\mu\not{a}\not{b}\not{c}\not{d}\gamma^\mu =
2[\not{d}\not{a}\not{b}\not{c} + \not{c}\not{b}\not{a}\not{d}]$](img4851.png) ,
,
-
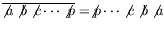 .
.
- Construct the amplitude for bremsstrahlung in electron-proton
scattering and show that the static limit reduces to
for bremsstrahlung in a Coulomb field.
Show that there is the same correspondence in factors between these
two cases as was found in
and
for elastic scattering.
- Derive the Bethe-Heitler cross-section for production of an
electron-positron pair by an incident photon in a Coulomb field.
Show that the amplitude for this is related to the bremsstrahlung
amplitude in equation (7.385) by the substitution rule.
- Calculate the cross-section for the absorption of light by a bound
electron in an atom with low atomic number
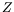 , such that
, such that
 and
and
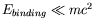 .
Assume also that the frequency of the light is such that
.
Assume also that the frequency of the light is such that
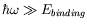 .
Making these simplifying assumptions calculate differential and total
cross-sections for the two limiting cases:
.
Making these simplifying assumptions calculate differential and total
cross-sections for the two limiting cases:
-
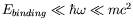 non-relativistic ,
non-relativistic ,
-
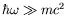 ultra-relativistic .
ultra-relativistic .
- Construct the differential cross-section for electron-electron
scattering in the lowest order Born approximation in terms of
laboratory energies and scattering angles.
- Show that the scattering matrix (S-matrix) is unitary.
- Derive the Bethe-Heitler cross-section for bremestrahlung of photons
of arbitrary energy.
- Verify that the inverse of the ``momentum space operator'' of
does not exist.
- In the center-of-mass frame for the process
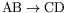 show that
show that
and hence that the differential cross-section is
where 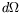 is the element of solid angle about
is the element of solid angle about 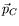 ,
,
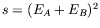 ,
,
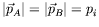 , and
, and
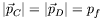 .
.
- Show that
where 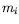 is the rest mass of particle
is the rest mass of particle 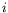 .
.
- Taking
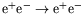 to be the
to be the 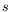 -channel
process, verify that
-channel
process, verify that
where 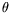 is the center-of-mass scattering angle and
is the center-of-mass scattering angle and
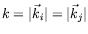 , where
, where 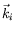 and
and 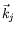 are, respectively, the momenta of the incident and scattered electrons
in the center-of-mass frame.
Show that the process is physically allowed provided
are, respectively, the momenta of the incident and scattered electrons
in the center-of-mass frame.
Show that the process is physically allowed provided 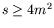 ,
,
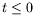 , and
, and 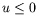 .
Note that
.
Note that 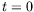 (
(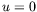 ) corresponds to the forward (backward) scattering
) corresponds to the forward (backward) scattering
- To show your understanding of QED, develope spinless QED.
Calculate
- compton scattering of bosons and
- electro-production of pion pairs.
- Rosenbluth's Formula.
The realistic description of the scattering of an electron at a spin-1/2
hardon has to take into account the internal structure and anomalous
magnetic moment of the hardon.
To that end one replaces the transition current in momentum space which
orignates from the Dirac equation with the more general bilinear
expression
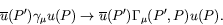 |
(7.385) |
- Show that the most general expression for a transition current
that fulfills the condition of Lorentz covariance, hermiticity, and
gauge invariance can be written as
![\begin{displaymath}
\overline{u}(P^\prime) \Gamma_\mu(P^\prime,P) u(P) =
\overli...
... + \frac{i}{2M} F_2(q^2)
q^\nu \sigma_{\mu\nu} \right] u(P) .
\end{displaymath}](img4892.png) |
(7.386) |
Here 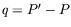 is the momentum transfer and
is the momentum transfer and
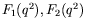 are
unspecified real functions (``form factors'').
are
unspecified real functions (``form factors'').
- What is the physical meaning of
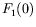 and
and 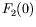 ?
This can be deduced by studying the interaction energy with static EM
fields in the nonrelativistic limit.
?
This can be deduced by studying the interaction energy with static EM
fields in the nonrelativistic limit.
- Calculate the unpolarized cross-section of electron scattering at a
hardon with vertex function above in the ultrarelativistic limit.
- Mandelstam variables applied to Møller and Bhabha scattering.
- Show that the kinematics of any binary scattering process
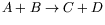 can be expressed in terms of the three
Lorentz-invariant Mandelstam variables.
can be expressed in terms of the three
Lorentz-invariant Mandelstam variables.
Prove the identity
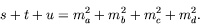 |
(7.390) |
- Derive the differential cross-section for electron-electron and
electron-positron scattering in terms of the Mandelstam variables.
Do not neglect the electron mass in this calculation.
- Write down explicit results for the Møller and Bhabha cross-sections in
the centre-of-mass system and in the laboratory system.
- Degree of polarization.
Calculate the differential scattering cross-section
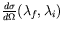 for Coulomb scattering of
electrons with longitudinal polarization.
Derive the degree of polarization
for Coulomb scattering of
electrons with longitudinal polarization.
Derive the degree of polarization  as a function of the scattering
angle.
as a function of the scattering
angle.
- Derive the differential and total unpolarized cross-sectiion for pair
annhilation
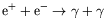 in the
centre-of-mass frame.
in the
centre-of-mass frame.
- Derive the total unpolarized cross-section for creation of an
electron-positron pair by two colliding photons,
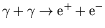 .
Express the result in terms of the velocity of the produced particles in
the centre-of-mass frame.
Hint: use the result for pair annhilation cross-section.
.
Express the result in terms of the velocity of the produced particles in
the centre-of-mass frame.
Hint: use the result for pair annhilation cross-section.
- Calculate the cross-section of electron-positron pair creation by an
incoming photon in the field of a heavy nucleus with charge
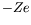 .
Hint: the calculation can be considereably simplified by exploting
crossing symmetry which relates pair creation and bremsstrahlung.
.
Hint: the calculation can be considereably simplified by exploting
crossing symmetry which relates pair creation and bremsstrahlung.
- Show that the
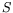 -matrix is symmetric under charge conjugation.
-matrix is symmetric under charge conjugation.
- We derived the laboratory frame cross-section for scattering of a high
energy electron from an ``ideal'' (structureless) proton.
However, the proton matrix element of the electromagnetic current was
assumed to have the naive form.
In reality one should use the current matrix element
where 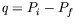 is the momentum transfer,
is the momentum transfer, 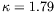 is the
anomalous magnetic moment of the proton, and
is the
anomalous magnetic moment of the proton, and 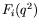 are form
factors which account for the finite hadronic size.
are form
factors which account for the finite hadronic size.
- Calculate the high energy laboratory cross-section for
electron-proton scattering using the full current element and show
that
where
- Verify that this expression reduces to that given earlier in the limit
that
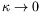 and
and
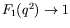 .
.
This is the Rosenbluth cross-section which has been used in order to
map out nuclear and particle charge distributions via electron
scattering.
- Suppose in our formalism we replace the vacuum by a Fermi gas with
Fermi momentum
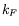 .
How is the Feynman propagator modified?
Compute the change in
.
How is the Feynman propagator modified?
Compute the change in 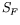 in the low-density limit.
in the low-density limit.
- Show that the rate for an electron in the hydrogen-atom ground state
to radiate and fall into empty negative-energy states (treated in Born
approximation) in the energy interval
 to
to 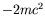 is
approximately
is
approximately
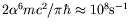 .
.
![]() to show that
to show that
![]() is a scalar
and that
is a scalar
and that
![]() is the time component of a vector,
as desired.
is the time component of a vector,
as desired.
![$\textrm{Tr}[\gamma_5\not{a}\not{b}] = 0$](img4848.png) ,
,
![$\textrm{Tr}[\gamma_5\not{a}\not{b}\not{c}\not{d}] =
4i\epsilon_{\alpha\beta\gamma\delta}a^\alpha b^\beta c^\gamma
d^\delta$](img4849.png) ,
,
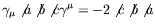 ,
,
![$\gamma_\mu\not{a}\not{b}\not{c}\not{d}\gamma^\mu =
2[\not{d}\not{a}\not{b}\not{c} + \not{c}\not{b}\not{a}\not{d}]$](img4851.png) ,
,
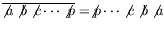 .
.
![\begin{eqnarray*}
S_{fi} & = & \frac{-ie^2}{V^2} (2\pi)^4 \delta^4(P_f-P_i+p_f-p...
...p_i)^2+i\epsilon} [\overline{u}(P_f,S_f) \gamma^\mu
u(P_i,S_i)]
\end{eqnarray*}](img4859.png)
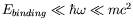 non-relativistic ,
non-relativistic ,
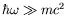 ultra-relativistic .
ultra-relativistic .
![]() is the element of solid angle about
is the element of solid angle about ![]() ,
,
![]() ,
,
![]() , and
, and
![]() .
.
![]() is the rest mass of particle
is the rest mass of particle ![]() .
.
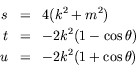
![]() is the center-of-mass scattering angle and
is the center-of-mass scattering angle and
![]() , where
, where ![]() and
and ![]() are, respectively, the momenta of the incident and scattered electrons
in the center-of-mass frame.
Show that the process is physically allowed provided
are, respectively, the momenta of the incident and scattered electrons
in the center-of-mass frame.
Show that the process is physically allowed provided ![]() ,
,
![]() , and
, and ![]() .
Note that
.
Note that ![]() (
(![]() ) corresponds to the forward (backward) scattering
) corresponds to the forward (backward) scattering
![\begin{displaymath}
\overline{u}(P^\prime) \Gamma_\mu(P^\prime,P) u(P) =
\overli...
... + \frac{i}{2M} F_2(q^2)
q^\nu \sigma_{\mu\nu} \right] u(P) .
\end{displaymath}](img4892.png)
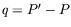 is the momentum transfer and
is the momentum transfer and
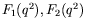 are
unspecified real functions (``form factors'').
are
unspecified real functions (``form factors'').
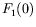 and
and 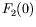 ?
This can be deduced by studying the interaction energy with static EM
fields in the nonrelativistic limit.
?
This can be deduced by studying the interaction energy with static EM
fields in the nonrelativistic limit.
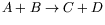 can be expressed in terms of the three
Lorentz-invariant Mandelstam variables.
can be expressed in terms of the three
Lorentz-invariant Mandelstam variables.
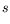
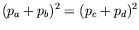
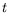
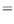
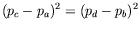
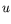
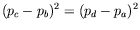
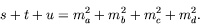
![]() is the momentum transfer,
is the momentum transfer, ![]() is the
anomalous magnetic moment of the proton, and
is the
anomalous magnetic moment of the proton, and ![]() are form
factors which account for the finite hadronic size.
are form
factors which account for the finite hadronic size.
![\begin{eqnarray*}
\frac{d\sigma}{d\Omega} & = &
\frac{\alpha^2\cos^2\theta/2}{4...
...\tan^2\theta/2 + \kappa^2 \vert F_2(q^2)\vert^2 \right] \right\}
\end{eqnarray*}](img4918.png)
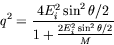
 and
and
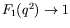 .
.